Lugares geométricos (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 191)
Lugar geométrico
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
A continuación vamos a ver algunos ejemplos de lugares geométricos: la mediatriz de un segmento, la bisectriz de un ángulo, la circunferenci o el arco capaz.
Mediatriz de un segmento
La mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan de sus extremos. Así, dado el segmento
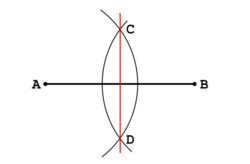
En esta escena podrás ver como construye la mediatriz de un segmento. |
Propiedad
La mediatriz de un segmento es una recta perpendicular al segmento que pasa por su punto medio.
Para hallar la ecuación de la mediatriz AB, siendo 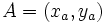 y
y 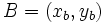 tenemos que hallar la ecuación del lugar geométrico
tenemos que hallar la ecuación del lugar geométrico
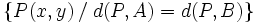
Para ello escribiremos la fórmula de la distancia entre dos puntos:
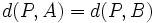
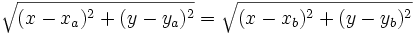
Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación:
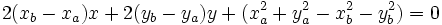
Por tanto, la ecuación de la mediatriz del segmento AB es la ecuación de una recta.
Faltaría ver que es perpendicular al segmento y que pasa por su punto medio.Bisectriz del ángulo entre dos rectas
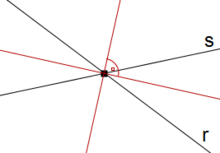
La bisectriz de un ángulo que forman las rectas es el lugar geométrico de los puntos del plano que equidistan de sus lados. Así, la bisectriz del ángulo que forman dos rectas,
Por como se ha definido la bisectriz, ésta divide al ángulo que forman las rectas en dos ángulos iguales. Además, como dos rectas determinan dos parejas de ángulos iguales, todo par de rectas determinan dos bisectrices. En esta escena podrás ver las bisectrices de los ángulos entre dos rectas. |
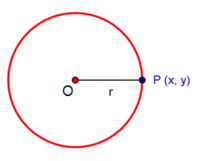
Circunferencia
La circunferencia de centro
En esta escena podrás ver como se dibuja una circunferencia. |
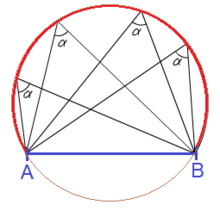
Arco capaz
| Observa los ángulos de la imagen de la derecha. Todos ellos son ángulos inscritos que abarcan un mismo arco de circunferencia. En consecuencia, sabemos que todos ellos son iguales.
Esto nos permite dar la siguiente definición: El arco capaz de un ángulo Esta escena te servirá para comprender el concepto de arco capaz. Escena en la que verás como se construye el arco capaz con regla y compás. Construcción con regla y compás del arco capaz de ángulo C dado un segmento AB. |
Ejercicios propuestos
|
Ejercicios propuestos: Lugares gemétricos |
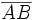 , su mediatriz está formada por los puntos
, su mediatriz está formada por los puntos  del siguiente conjunto:
del siguiente conjunto:
 y
y 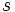 , está formada por los puntos
, está formada por los puntos 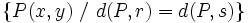
 y radio
y radio 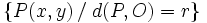
 para un segmento
para un segmento  .
.