Plantilla:Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas
De Wikipedia
[editar]
Funciones trigonométricas
Si recordamos las propiedades de las funciones trigonométricas, tenemos:
Propiedades
- Las funciones
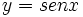 ,
, 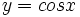 e
e 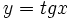 , por ser periódicas, no tienen límite cuando
, por ser periódicas, no tienen límite cuando  ni cuando
ni cuando 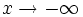 . Por tanto no tienen ramas parabólicas, ni asíntotas horizontales. Las dos primeras tampoco tienen asíntotas verticales por ser su dominio los números reales.
. Por tanto no tienen ramas parabólicas, ni asíntotas horizontales. Las dos primeras tampoco tienen asíntotas verticales por ser su dominio los números reales.
- La función
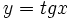 , tiene infinitas asíntotas verticales en los puntos
, tiene infinitas asíntotas verticales en los puntos
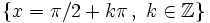
[editar]
Funciones exponenciales
Si recordamos las propiedades de las funciones exponenciales, tenemos:
Propiedades
La función 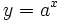 tiene:
tiene:
- Asíntota horizontal:
- En
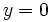 para
para  si
si 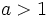
- En
- En
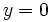 para
para  si
si 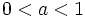
- En
- Rama parabólica:
- Para
 si
si 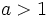
- Para
- Para
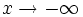 si
si 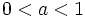
- Para
- Asíntota vertical: No tiene, pués es continua en toda la recta real.
[editar]
Funciones logartmicas
Si recordamos las propiedades de las funciones logarítmicas, tenemos:
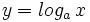 tiene:
tiene:
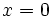 , cuando
, cuando 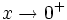 .
.

