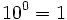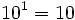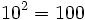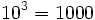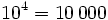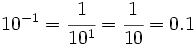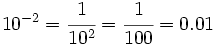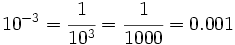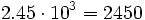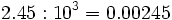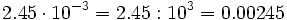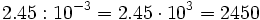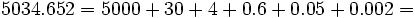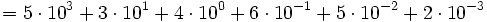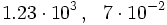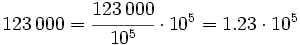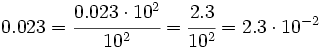Potencias de base 10. Notación científica (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 81)
Potencias de base 10
| Potencias de exponente positivo:
| Potencias de exponente negativo:
|
El exponente de las potencias de base 10:
En la siguiente escena, modifica los valores del exponente y observa qué sucede en los siguientes casos:
- Si el exponente es cero
- Si el exponente es positivo
- Si el exponente es negativo
Anota tus conclusiones en tu cuaderno.
Paso de forma decimal a potencia de base 10:
Introduce la respuesta adecuada.
Antes de empezar consulta la ayuda que tiene la escena.
Anota en tu cuaderno los ejercicios.
Paso de potencia de base 10 a forma decimal:
Introduce la respuesta adecuada.
Antes de empezar consulta la ayuda de la escena.
Anota en tu cuaderno los ejercicios.
Universo, macro y microcosmos en potencias de 10.
Universo, macro y microcosmos en potencias de 10.
Observa la Vía Lactea desde 10 millones de años luz de distancia a la Tierra. Ve aproximándote a ésta progresivamente, hasta llegar a un árbol que hay en la superficie. Penetra en el mundo microscópico de una de sus hojas hasta llegar al universo subatómico de electrones y protones.
Universo, macro y microcosmos en potencias de 10
Operaciones con potencias de base 10
Procedimiento
- Al multiplicar un número por
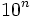 :
:
- Si
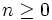 , el número resultante se obtiene desplazando la coma hacia la derecha
, el número resultante se obtiene desplazando la coma hacia la derecha  posiciones.
posiciones.
- Si
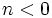 , el número resultante se obtiene desplazando la coma hacia la izquierda
, el número resultante se obtiene desplazando la coma hacia la izquierda  posiciones.
posiciones.
- Si
- Al dividir un número por
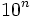 :
:
- Si
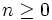 , el número resultante se obtiene desplazando la coma hacia la izquierda
, el número resultante se obtiene desplazando la coma hacia la izquierda  posiciones.
posiciones.
- Si
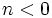 , el número resultante se obtiene desplazando la coma hacia la derecha
, el número resultante se obtiene desplazando la coma hacia la derecha  posiciones.
posiciones.
- Si
- Nota 1: En todos los casos, al desplazar la coma, se añadirán los ceros que sean necesarios.
- Nota 2: Dividir por
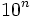 equivale a multiplicar por
equivale a multiplicar por 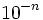 .
.
Tutorial que explica a través de ejercicios la multiplicación y división de números decimales por potencias de 10, tanto de exponente positivo como negativo.
- Reglas para multiplicar o dividir un número racional por potencias de 10. Ejemplos.
- Ejercicios resueltos.
Calcula: 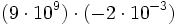
Productos y cocientes de múltiplos de potencias de 10
Descomposición polinómica de un número
La descomposición polinómica de un número consiste en expresar dicho número como una suma, en la que cada sumando es cada cifra del número multiplicada por una potencia de 10, cuyo exponente es una unidad menos de la posición que ocupa la cifra que la multiplica.
Ya conoces del curso pasado la descomposición polinómica de un número natural:
Ver: Descomposición polinómica de un número natural
A continuación veremos como se descompone un número decimal:
Procedimiento
Para descomponer polinómicamente un número decimal procederemos de la siguiente manera:
- La parte entera del número se descompone como se hace con los números naturales, utilizando potencias de exponente positivo, teniendo en cuenta las equivalencias:
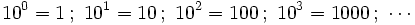
- La parte decimal del número se descompone de forma análoga pero utilizando potencias de exponente negativo, teniendo en cuenta las siguientes equivalencias:
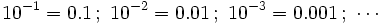
Notación científica
Trabajar con números muy grandes o muy pequeños (muy próximos a cero) resulta engorroso. Por eso debemos aprender a escribir estos números de una forma más abreviada y que resulte más cómoda.
Esta forma de escribirlos es lo que llamaremos notación científica. Veamos en qué consiste:
Un número está en notación científica si aparece expresado de la forma:
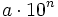
donde  es un número con 1 cifra entera distinta de cero y un número cualquiera de decimales.
es un número con 1 cifra entera distinta de cero y un número cualquiera de decimales.
Ejemplo 1:
- Los siguientes números están en notación científica:
- Estos otros no lo están:
Ejemplo 2:
- La distancia media de la Tierra al Sol es de unos 1500 millones de kilómetros. Si tuviésemos que expresarlo en metros, lo podríamos escribir con todas sus cifras, pero sería más razonable escribirlo en notación científica:
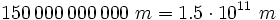
- La masa de un electrón es aproximadamente
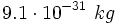 . Si lo escribiésemos con todas sus cifras ...
. Si lo escribiésemos con todas sus cifras ...
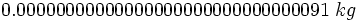
En la siguiente escena, genera distintos números, pulsando el botón inferior.
Anótalos en tu cuaderno, explicando qué condiciones cumple para que esté en notación científica.
Consulta la ayuda de la escena y contesta.
Modifica los valores de las cifras y del exponente y observa qué sucede con la coma en los siguientes casos:
- Si el exponente es cero
- Si el exponente es negativo
- Si el exponente es positivo
Anota en tu cuaderno las conclusiones a las que hayas llegado.
Consulta la ayuda de la escena y contesta.
Debes averiguar qué números son menores que 1 (numeros pequeños) o mayores que 1 (números grandes).
Anota en tu cuaderno los resultados.
Para comparar números escritos en notación científica debes tener en cuenta las siguientes normas:
- Dos números con distinta potencia de 10 : el nº mayor es el de mayor exponente
- Dos números con la misma potencia de 10: el nº mayor es el de "mayor cifra" delante de la potencia
Consulta la ayuda y practica con la escena adjunta.
Anota en tu cuaderno los resultados.
Procedimiento
Para pasar un número a notación científica debemos:
- Desplazar la coma hasta colocarla detrás de la primera cifra distinta de cero.
- Multiplicar por una potencia de 10 adecuada:
- Si la desplazamos
 lugares a la izquierda, estamos dividiendo el número de partida por
lugares a la izquierda, estamos dividiendo el número de partida por 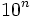 , por lo que deberemos multiplicar por
, por lo que deberemos multiplicar por 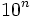 para equilibrar.
para equilibrar.
- Si la desplazamos
 lugares a la derecha, estamos multiplicando el número de partida por
lugares a la derecha, estamos multiplicando el número de partida por 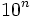 , por lo que deberemos dividir por
, por lo que deberemos dividir por 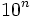 para equilibrar, esto es, multiplicar por
para equilibrar, esto es, multiplicar por 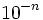 .
.
- Si la desplazamos
Expresa en notación científica los siguientes números:
- a) 123 000 b) 0.023
Solución:
a) Para expresar 123 000 en notación científica debemos mover la coma 5 lugares hacia la izquierda para que quede situada entre el 1 y el 2. (Nótese que la coma está detrás del último cero en el número de partida, aunque no se escribe). Esto equivale a dividir el número de partida entre 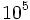 , por lo que compensaremos multiplicando por dicha potencia:
, por lo que compensaremos multiplicando por dicha potencia:
b) Para expresar 0.023 en notación científica debemos mover la coma 2 lugares hacia la derecha para que quede situada entre el 2 y el 3. Esto equivale a multiplicar el número de partida por 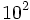 , por lo que compensaremos dividiendo por dicha potencia:
, por lo que compensaremos dividiendo por dicha potencia:
Números en notación científica. Ejemplos.
Potencias de 10 y notación científica. Ejemplos.
Introducción a la notación científica.
Escribe en notación científica:
a) 12 670 000 000 kg
b) 92 000 m
c) 0.000 632 km3
d) 0.048 hm
Escribe en notación científica:
a) 407 000 000 000 000
b) 24 000
c) 0.000 000 078
Escribe en notación científica:
a) 5 000 000 000 b) 27 000 c) 900 d) 129 000
e) 0.000 000 025 f) 0.000 678 g) 0.000 000 000 000 853
Escribe 0.0000000003457 en notación científica.
Escribe en notación científica:
- a) 0.00852 b) 7 012 000 000 000 c) 0.0000000000000500
- d) 723 e) 0.6 f) 82 300 000 000
Opera pasando previamente a notación científica cuando sea necesario:
- a)
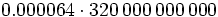
- b)

Escribe con todas sus cifras:
- a)
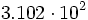 b)
b) 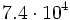 c)
c) 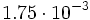 d)
d) 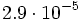
Escribe en notación científica:
- a) 120 000 b) 1 765 244 c) 12 d) 0.00281 e) 0.000000027
Actividades para aprender a manejar la notación científica.
- Ejemplos de números muy grandes y muy pequeños.
- Ejercicios resueltos sobre notación científica. Uso de la calculadora.
Repaso sobre notación científica.
Escribe en notación científica.
Escribe en noptación científica.
Notación científica.
Ejercicios propuestos
|
Ejercicios propuestos: Potencias de 10. Notación científica |