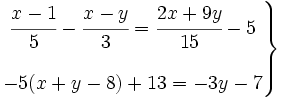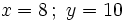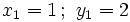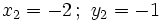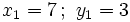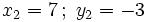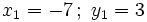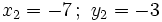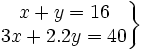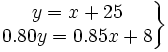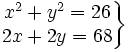Resolución de sistemas lineales y no lineales (3ºESO Académicas)

De Wikipedia

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Reglas para resolver sistemas lineales
2 Resolución de sistemas no lineales
- 2.1 Ejercicios propuestos
3 Resolución de problemas mediante sistemas
- 3.1 Ejercicios propuestos

(Pág. 131)

[editar]

Reglas para resolver sistemas lineales

Procedimiento

Para resolver un sistema de ecuaciones lineales podemos proceder de la siguiente forma:

Transformar las ecuaciones del sistema hasta que tengan la forma 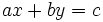$ax+by=c\;$ . Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
Elegir un método de resolución adecuado: el método de sustitución es cómodo si alguna incógnita tiene coeficiente 1 o -1; el de reducción es cómodo si alguna incógnita tiene el mismo coeficiente en las dos ecuaciones o sus coeficientes son uno múltiplo del otro; el de igualación es cómodo por su mecánica de despejar, igualar y multiplicar en cruz.
Podemos, opcionalmente, comprobar las soluciones. Para ello sustituiremos las incógnitas por los valores obtenidos en las dos ecuaciones del sistema de partida y los resultados deben coincidir.

Ejercicio resuelto

Resuelve el siguiente sistema:

$\left . \begin{matrix} \cfrac{x-1}{5}-\cfrac{x-y}{3}=\cfrac{2x+9y}{15}-5 \\~ \\ -5(x+y-8)+13=-3y-7 \end{matrix} \right \}$

Solución:

Solución: $x=8\,; \ y=10$

Ejercicios resueltos Descripción:

Ejercicios de autoevaluación sobre resolución de sistemas lineales.

[editar]

Resolución de sistemas no lineales

Para resolver sistemas no lineales también podemos usar lo que sabemos sobre resolución de ecuaciones no lineales junto con los métodos de resolución de sistemas lineales conocidos (sustitución, igualación y reducción).

Ejercicios resueltos:

Resuelve los siguientes sistemas:

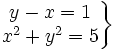
1. $\left . \begin{matrix} y-x=1 \\ x^2+y^2=5 \end{matrix} \right \}$

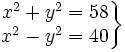
2. $\left . \begin{matrix} x^2+y^2=58 \\ x^2-y^2=40 \end{matrix} \right \}$

Solución:

Soluciones:

1. Tiene dos soluciones:

$x_1=1 \, ; \ y_1=2$

$x_2=-2 \, ; \ y_2=-1$

2. Tiene cuatro soluciones:

$x_1=7 \, ; \ y_1=3$

$x_2=7 \, ; \ y_2=-3$

$x_1=-7 \, ; \ y_1=3$

$x_2=-7 \, ; \ y_2=-3$

Ejercicios (6'59") Sinopsis:

Cuatro sistemas no lineales de ecuaciones.

[editar]

Ejercicios propuestos

Ejercicios y problemas propuestos: Resolución de sistemas no lineales

(Pág. 132)

[editar]

Resolución de problemas mediante sistemas

Procedimiento

Para resolver un problema mediante sistemas de ecuaciones hay que seguir los siguientes pasos:

Determinar las incógnitas.
Traducir el enunciado del problema al lenguaje algebraico mediante ecuaciones en las que intervengan las incógnitas.
Resolver el sistema, es decir, hallar el valor de las incógnitas.
Dar la solución del problema a partir de los valores obtenidos de las incógnitas.

Ejercicios resueltos

Dos estaciones A y B distan 255 km. Un tren sale de A hacia B a una velocidad constante de 60 km/h. Simultáneamente, sale de B hacia A otro tren a 110 km/h. Calcular el tiempo que tardan en cruzarse y la distancia que ha recorrido cada uno hasta ese instante.
Un bodeguero ha mezclado dos garrafas de vino. La primera, de mejor calidad, a 3 €/l y la segunda, de claidad inferior, a 2.20 €/l. De esta forma ha obtenido 16 l de un vino de calidad intermedia que sale a 2.50 €/l. ¿Qué cantidad de vino había en cada garrafa?
Mariluz ha comprado un abrigo que estaba rebajado un 15%. Jorge ha comprado otro abrigo 25 € más caro, pero ha conseguido una rebaja del 20%, con lo que sólo ha pagado 8 € más que Mariluz. ¿Cuál era el precio original de cada abrigo?
La diagonal de un rectángulo mide 26 m, y el perímetro, 68 m. Calcula la medida de sus lados.

Solución:

Solución 1:

x = distancia de A al punto de encuentro de los dos trenes.

255-x = distancia de B al punto de encuentro de los dos trenes.

Primer tren: $x = 60t\;$

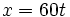
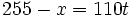
Segundo tren: $255-x=110t\;$

Sol: x = 90 ; t = 1.5

Los trenes se encuentran 1h 30 min después de salir. El primer tren recorre 90 km y el segundo 165 km.

Solución 2:

x = litros de vino de mejor calidad

y = litros de vino de calidad inferior

$\left . \begin{matrix} x+y=16 \\ 3x+2.2y=40 \end{matrix} \right \}$

Sol: x = 6 ; y = 10

Había 6 l en la primera garrafa y 10 l en la segunda.

Solución 3:

x = precio del abrigo de Mariluz sin rebajar

y = precio del abrigo de Jorge sin rebajar

$\left . \begin{matrix} y=x+25 \\ 0.80y=0.85x+8 \end{matrix} \right \}$

Sol: x = 240 ; y = 265

El abrigo de Mariluz costaba 240 € y el de Jorge 265 €.

Solución 4:

x = base del rectángulo

y = altura del rectángulo

$\left . \begin{matrix} x^2+y^2=26 \\ 2x+2y=68 \end{matrix} \right \}$

El sistema tiene dos soluciones:

x = 24 ; y = 10

x = 10 ; y = 24

Ambas dan un mismo rectángulo de lados 24 m y 10 m.

Resolución de problemas mediante sistemas de ecuaciones lineales

Problemas 1 (9'22") Sinopsis:

Resolución de problemas mediante sistemas de ecuaciones.

Problemas 2 (16'26") Sinopsis:

Tutorial practico en el que aparecen dos problemas resueltos mediante ecuaciones. Estos problemas son del tipo en el que aparecen distintos elementos (vacas/avestruces, monedas 1€/2€, aciertos/fallos...) que juntos aportan un total de algo (patas, dinero, puntuación...).

Problema 3 (11'11") Sinopsis:

Resolución de problemas empleando sistemas de ecuaciones no lineales.

Problema 4 (11'44") Sinopsis:

Por tres adultos y cinco niños se pagan 190€ para entrar en un parque de atracciones. Si son cuatro adultos y siete niños, el valor es de 260€.¿Cuál es el valor de cada entrada?

Problema 5 (4'05") Sinopsis:

Resolución de problemas de números mediante sistemas de ecuaciones lineales.

Problema 6 (8'42") Sinopsis:

Resolución de problemas de edades mediante sistemas de ecuaciones lineales.

Problema 7 (8'58") Sinopsis:

Resolución de problemas de invertir las cifras de un número mediante sistemas de ecuaciones lineales.

Problema 8 (10'15") Sinopsis:

Resolución de problemas de invertir las cifras de un número mediante sistemas de ecuaciones lineales.

Problema 9a (edades) (5'26") Sinopsis:

Un padre es 4 veces mayor que sus hijo. En 24 años más, él tendrá el doble de la edad de su hijo. ¿Cuál es la edad actual del hijo?

Problema 9b (edades) (5'36") Sinopsis:

Juan le dice a su hermano Pedro: hace tres años yo era cuatro veces más viejo que tú, pero dentro de cinco, sólo te doblaré en edad. ¿Cuántos años tienen?

Problema 10 (geometría) (5'33") Sinopsis:

Se tienen dos cuadrados distintos. El lado de uno de ellos es 4 cm mayor que el del otro. Averigua la longitud de los lados de ambos cuadrados sabiendo que la suma de sus áreas es de 80 cm ².

Problema 11 (números) (4'37") Sinopsis:

Dos números suman 51. Si el primero lo dividimos entre 3 y el segundo entre 6, la diferencia de sus cocientes es 1. Halla los números.

Problema 12 (mezclas) (5'54") Sinopsis:

Con dos clases de café de 900 pts/kg y 1200 pts/kg, se quiere obtener una mezcla de 1000 pts/kg. (pts=pesetas) Halla las cantidades que hay que mezclar para obtener 30 kg de mezcla.

Problema 13 (cifras) (5'49") Sinopsis:

La suma de las dos cifras de un número es 8. Si al número le añades 18 unidades, el número resultante está formado por las mismas cifras pero en orden inverso. Halla el número.

Problemas 14 (7´06") Sinopsis:

Juan y María son hermanos. El tiene tantos hermanos como hermanas, y ella tiene doble número de hermanos que de hermanas. ¿Cuántos hermanos hay de cada sexo?
Determina las dimensiones de un rectángulo sabiendo que su área aumenta 600 m² al duplicar los lados, aumentando 340 m² si la base disminuye 2 m y la altura se triplica.

Problemas 15 (7´03") Sinopsis:

Determina un número de dos dígitos sabiendo que es el cuádruplo de la suma de éstos, y que al invertir el orden de los dígitos, aumenta 36 unidades.
Determina un número de dos dígitos sabiendo que la suma de ambos es 11, y que al invertir el orden de los dígitos, resulta un número que se diferencia en 36 unidades del primero.

Problema 16a (6'54") Sinopsis:

Un gnomo tiene 900 monedas entre monedas de 5 y 10 pesos con un valor total de 5500 pesos. ¿Cuántas monedas tiene de cada tipo? (1ª parte: El planteamiento)

Problema 16b (5'44") Sinopsis:

Un gnomo tiene 900 monedas entre monedas de 5 y 10 pesos con un valor total de 5500 pesos. ¿Cuántas monedas tiene de cada tipo? (2ª parte: resolución por el método gráfico)

Problema 17 (9'03") Sinopsis:

A un banquete asistieron 500 adultos y 200 niños y se comieron 2900 pasteles. A otro banquete asistieron 500 adultos y 300 niños y comieron 3100 pasteles. Sabiendo que cada niño o cada adulto comió la misma cantidad de pasteles en ambos banquetes, calcula el número de pasteles que comió cada adulto y el número de pasteles que comió cada niño. (Método de reducción)

Problema 18a (9'25") Sinopsis:

A un banquete asistieron 200 hombres y 300 mujeres y se comieron 1200 bolsas de patatas fritas. A otro banquete asistieron 100 hombres y 400 mujeres y comieron 1100 bolsas de patatas fritas. Sabiendo que cada hombre o cada mujer comió la misma cantidad de bolsas de patatas en ambos banquetes, calcula el número de bolsas que comió cada hombre y el número de bolsas que comió cada mujer. (Método de reducción)

Problema 18b (5'24") Sinopsis:

Problema 19a (9'26") Sinopsis:

Un día fuimos al mercado y compramos 2 kg de manzanas y 1 kg de plátanos por 3 pesos. Otro día compramos 6 kg de manzanas y 3 kg de plátanos y pagamos 15 pesos. Averigua a cómo está cada una de las frutas. (Problema sin solución)

Problema 19b (7'08") Sinopsis:

Un día fuimos al mercado y compramos 2 kg de manzanas y 1 kg de plátanos por 5 pesos. Otro día compramos 6 kg de manzanas y 3 kg de plátanos y pagamos 15 pesos. Averigua a cómo está cada una de las frutas. (Problema con infinitas soluciones)

Problema 20 (6'30") Sinopsis:

Vicente tiene 4 veces la edad de Alex. Hace 12 años, Vicente tenía 7 veces la edad de Alex. ¿Cuál es la edad actual de Alex?

Problema 21 (5'24") Sinopsis:

Armando tiene 18 años y Diana 2 años. ¿En cuántos años Armando tendrá el triple de edad que Diana?

Problema 22 (8'13") Sinopsis:

Juanito caminó desde su casa a la parada del autobús a una velocidad media de 5 km/h. El subió de inmediato a su autobús y viajó a una velocidad media de 60 km/h hasta que llegó a su escuela. La distancia total de su casa a la escuela es de 35 km y todo el viaje duró 1.5 horas. ¿Cuántos kilómetros caminó Juanito y cuántos recorrió en autobús?

Problema 23 (6'05") Sinopsis:

Una fábrica tiene máquinas que producen juguetes y que son empaquetados por los trabajadores de la fábrica. Un día cada máquina produce 14 juguetes y cada trabajador empaqueta 2, por lo que un total de 40 juguetes queda sin empaquetar. Además ese día, el número de trabajadores era 8 menos que 7 veces el número de máquinas. ¿Cuántas máquinas y trabajadores había ese día?

Problema 24 (5'56") Sinopsis:

El granjero José cultiva vegetales y divide su campo entre cultivos de brócoli y cultivos de espinaca. El año pasado cosechó 6 toneladas de brócoli y 9 de espinaca por acre, que dieron un total de 93 toneladas de vegetales. Este año ha cosechado 2 toneladas de brócoli y 3 de espinaca por acre, para un total de 31 toneladas de vegetales. ¿Cuántos acres dedica al cultivo de brócoli y cuántos al de espinaca?

Problema 25 (5'53") Sinopsis:

Un almacén de electrónica envía televisores y reproductores DVD de manera combinada a distribuidores de todo el país. El peso de 3 televisores y 5 reproductores es de 62.5 libras y el peso de 3 televisores y 2 reproductores es de 52 libras. Averigua el peso de cada televisor y de cada reproductor.

Problema 26 (5'08") Sinopsis:

Imagínate que vas al mercado a conseguir un poco de fruta fresca. En el momento en el que vas a pagar te das cuenta de que el cliente que atendieron antes compró 5 manzanas y 4 naranjas por 10 pesos, mientras que tú compras 5 manzanas y 5 naranjas por 11 pesos. ¿Podemos encontrar el precio de cada manzana y de cada naranja? Si es que sí, ¿cuál es la solución?. Si es que no, ¿por qué no puedes resolverlo?.

Problema 27 (6'03") Sinopsis:

Como regalo de cumpleaños, Zoe le dio a su sobrina una hucha electrónica, la cual muestra la cantidad total de dinero que contiene, así como la cantidad total de monedas. Después de depositar cierta cantidad de monedas de 5 centavos y 25 centavos, la hucha mostró lo siguiente:

Dinero: $2
Número de monedas: 16

¿Cuántas monedas de cada tipo puso en la hucha?

Problema 28 (4'17") Sinopsis:

Imagina que estás en una cafetería de París, tomando un café con tu mejor amigo. A un francés en la mesa de al lado le cobran 5.30 € por una taza de café y un pan de dulce. después, cuando tú pides la cuenta, a ustedes os cobran 14 € por dos tazas de café y dos panes de dulce. ¿Puedes obtener el precio de la taza de café y del pan de dulce? Si es que sí, ¿cuál es la solución?. Si es que no, ¿por qué no puedes resolverlo?.

Resolución de problemas mediante sistemas de ecuaciones lineales

Actividad 1a Descripción:

Actividades en las que aprenderás y practicarás la resolución de problemas de distintos tipos mediante sistemas de ecuaciones lineales con dos incógnitas.

Actividad 1b Descripción:

Problemas resueltos mediante sistemas de ecuaciones lineales con dos incógnitas.

Autoevaluación Descripción:

Problemas que se resuelven mediante sistemas de ecuaciones lineales con dos incógnitas.

Problemas resueltos Descripción:

Problemas resueltos mediante sistemas de ecuaciones lineales con dos incógnitas.

[editar]

Ejercicios propuestos

Ejercicios y problemas propuestos: Resolución de problemas mediante sistemas

(Pág. 133-134)

1 al 5

Obtenido de "http://maralboran.org/wikipedia/index.php/Resoluci%C3%B3n_de_sistemas_lineales_y_no_lineales_%283%C2%BAESO_Acad%C3%A9micas%29"

Categorías: Matemáticas | Álgebra

Resolución de sistemas lineales y no lineales (3ºESO Académicas)

De Wikipedia

Tabla de contenidos

Reglas para resolver sistemas lineales

Resolución de sistemas no lineales

Ejercicios propuestos

Resolución de problemas mediante sistemas

Ejercicios propuestos

Vistas

Herramientas personales

Menú

Buscar

Herramientas