Ecuaciones de primer grado con dos incógnitas
De Wikipedia
| Revisión de 11:46 11 mar 2008 Coordinador (Discusión | contribuciones) (→Soluciones de una ecuación de primer grado con dos incógnitas) ← Ir a diferencia anterior |
Revisión de 17:22 13 dic 2008 Coordinador (Discusión | contribuciones) (→Ecuación de primer grado con dos incógnitas) Ir a siguiente diferencia → |
||
| Línea 66: | Línea 66: | ||
| '''Concluyendo: '''Las soluciones de una ecuación de primer grado con dos incógnitas son infinitas y los puntos que se obtienen con sus coordenadas, están situados en una recta. | '''Concluyendo: '''Las soluciones de una ecuación de primer grado con dos incógnitas son infinitas y los puntos que se obtienen con sus coordenadas, están situados en una recta. | ||
| }} | }} | ||
| - | {{p}} | + | {{p}}{{b}} |
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 17:22 13 dic 2008
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas es aquella que se puede expresar de la forma:
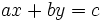
donde  e
e  son variables y
son variables y 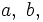 y
y  constantes.
constantes.
Ejemplo: 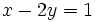
Soluciones de una ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas 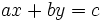 tiene infinitas soluciones.
tiene infinitas soluciones.
Para cada valor que le asignemos a la variable  , podemos encontrar un valor de la variable
, podemos encontrar un valor de la variable  , despejándola en la ecuación:
, despejándola en la ecuación:
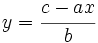
Además, las parejas de soluciones 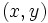 , representadas como puntos, en unos ejes de coordenadas, forman una recta.
, representadas como puntos, en unos ejes de coordenadas, forman una recta.
Ejemplo: Ecuación de primer grado con dos incógnitas
- Halla algunas soluciones para la ecuación:
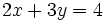
Despejamos la variable y:
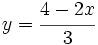
Construimos una tabla de valores, dandole valores a  y calculando
y calculando  en la expresión anterior:
en la expresión anterior:
| x | -1 | 2 | 5 | ... |
| y | 2 | 0 | -2 | ... |
Las soluciones vienen dadas por las parejas 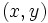 así obtenidas:
así obtenidas:
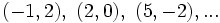
Si representamos estas soluciones como puntos de unos ejes de coordenadas, comprobaremos que se encuentran situados en una línea recta, como puedes ver en la siguiente escena.
Comprueba que los puntos solución se encuentran en la recta azul. Para ello deberás introducir el valor de  en el cuadro inferior y pulsar "Intro":
en el cuadro inferior y pulsar "Intro":
Calcula algunas soluciones más y compruébalas en la escena anterior.
Concluyendo: Las soluciones de una ecuación de primer grado con dos incógnitas son infinitas y los puntos que se obtienen con sus coordenadas, están situados en una recta.
