Funciones: Simetría
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:21 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 21: | Línea 21: | ||
| |width=50%|[[Imagen:impar.png|275px|center|thumb|Funcion impar: <math>y=x^3</math>]] | |width=50%|[[Imagen:impar.png|275px|center|thumb|Funcion impar: <math>y=x^3</math>]] | ||
| |} | |} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Simetría de funciones''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' Relaciona cada función con su tipo de simetría. | ||
| + | |actividad= | ||
| + | <center><iframe> | ||
| + | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010924_AC_0_158605500&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010924_AC_0_158605500&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | }} | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Coordenadas | Ejercicios 1 Ejercicios 2 | WIRIS Geogebra Calculadora Función Lista de funciones |
[editar]
Simetrías
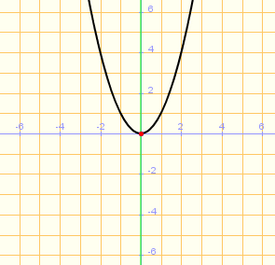
- Una función se dice que es par si se cumple que:
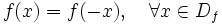
En tal caso su gráfica es simétrica respecto al eje de ordenadas.
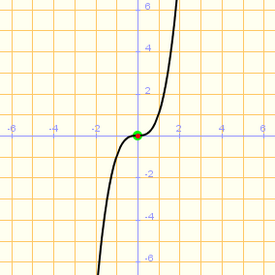
- Una función se dice que es impar si se cumple que:
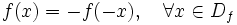
En tal caso su gráfica es simétrica respecto al origen de coordenadas.
|
Actividad Interactiva: Simetría de funciones
Actividad 1: Relaciona cada función con su tipo de simetría.
|