Divisibilidad

De Wikipedia

(Diferencia entre revisiones)

Revisión de 07:35 20 feb 2009

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Divisibilidad I Divisibilidad II	Divisibilidad m.c.m. m.c.d. Números sociables Números perfectos Números amigos Números compuestos Aritmética modular	WIRIS Geogebra Calculadora

Tabla de contenidos

1 Múltiplos y divisores
2 Criterios de divisibilidad
3 Números compuestos y números primos
- 3.1 Descomposición factorial de un número
- 3.2 Obtención de los divisores de un número
4 Máximo común divisor
- 4.1 Propiedad
- 4.2 Números primos entre sí
5 Mínimo común múltiplo
- 5.1 Propiedades
6 Ejercicios y problemas
- 6.1 Ejercicios
- 6.2 Problemas
7 Calculadora

Múltiplos y divisores

Plantilla:Múltiplos y divisores

Criterios de divisibilidad

Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división.

Divisible por:	Criterio
2	El número acaba en 0 ó cifra par.
3	La suma de sus cifras es un múltiplo de 3.
4	El número formado por las dos últimas cifras es múltiplo de 4.
5	La última cifra es 0 ó 5.
6	El número es divisible por 2 y por 3.
7	La diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7.
8	El número formado por las tres últimas cifras es múltiplo de 8.
9	La suma de sus cifras es múltiplo de 9.
10	La última cifra es 0.
11	Se suman las cifras que forman el número de forma alternativa y se restan los resultados para ver si da un múltiplo de 11 (El cero también lo es)

Observación:

Los números que aparecen en verde se corresponden con aquellos cuyo criterio es un proceso que se puede usar de forma recursiva, es decir, si después de aplicarlo no sabemos si el número al que hemos llegado es múltiplo del número en cuestión, podemos aplicar nuevamente el criterio sobre ese resultado.

Criterios de divisibilidad

Criterios de divisibilidad por 2, 3 y 5 (3´26") Sinopsis:

Criterios de divisibilidad por 2, 3 y 5. Ejemplos.

Criterios de divisibilidad por 2, 3, 5, 10 y 11 (8'08") Sinopsis:

Criterios para averiguar si un número es divisible por 2, 3, 5, 10 u 11. Ejemplos.

Criterios de divisibilidad por 2, 3, 5, 9 y 11 (7'35") Sinopsis:

Criterios para averiguar si un número es divisible por 2, 3, 5, 9 u 11. Ejemplos.

Criterios de divisibilidad por 2, 3, 4, 5 y 6 (3´28") Sinopsis:

Criterios de divisibilidad por 2, 3, 4, 5 y 6. Ejemplos.

Criterios de divisibilidad por 7, 8, 9, 10 y 11 (4´36") Sinopsis:

Criterios de divisibilidad por 7, 8, 9, 10 y 11. Ejemplos.

Criterios de divisibilidad por 2, 3, 4, 5, 6, 7, 8, 9, 10 y 11 (14´50") Sinopsis:

Criterios de divisibilidad por 2, 3, 4, 5, 6, 7, 8, 9, 10 y 11. Ejemplos.

Criterios de divisibilidad por 2, 3, 5, 7, 11 y 10ⁿ (24´50") Sinopsis:

Tutorial que explica los criterios de divisibilidad más básicos e importantes, es decir los "trucos" para saber, sin necesidad de dividir, si 2, 3, 5, 7, 11 y 10ⁿson divisores de un número.

00:00 a 04:20: Definiciones básicas (divisor).
04:20 a 05:55: Criterio de divisibilidad del 2.
05:55 a 07:05: Criterio de divisibilidad del 5.
07:05 a 09:50: Criterio de divisibilidad de potencias de 10.
09:50 a 15:27: Criterio de divisibilidad del 3.
15:27 a 21:00: Criterio de divisibilidad del 11.
21:00 a 24:50: Criterio de divisibilidad del 7.

Criterios de divisibilidad por 6, 2ⁿ, 5ⁿ, 9 (15´46") Sinopsis:

Tutorial que explica algunos criterios de divisibilidad más, es decir los "trucos" para saber, sin necesidad de dividir, si 6, 2ⁿ, 5ⁿ y 9 son divisores de un número.

00:00 a 02:20: Definiciones básicas (divisor).
02:20 a 05:15: Criterio de divisibilidad de las potencias de 2.
05:15 a 07:15: Criterio de divisibilidad de las potencias de 5.
07:15 a 10:30: Criterio de divisibilidad del 9.
10:30 a 15:46: Criterio de divisibilidad del 6 o producto de primos.

Criterio de divisibilidad por 3 (explicación) (8'06") Sinopsis:

Explicación de por qué funciona el criterio de divisibilidad por 3.

Criterio de divisibilidad por 9 (explicación) (8'13") Sinopsis:

Explicación de por qué funciona el criterio de divisibilidad por 9.

Ejemplo 1 (0'41") Sinopsis:

Criterios de divisibilidad por 2

Ejemplo 2 (0'58") Sinopsis:

Criterios de divisibilidad por 3

Ejemplo 3 (0'49") Sinopsis:

Criterios de divisibilidad por 4

Ejemplo 4 (0'30") Sinopsis:

Criterios de divisibilidad por 5

Ejemplo 5 (0'42") Sinopsis:

Criterios de divisibilidad por 9

Ejemplo 6 (0'25") Sinopsis:

Criterios de divisibilidad por 10

Ejemplo 7 (1'45") Sinopsis:

Criterios de divisibilidad por 11

Ejercicio 1 (12'04") Sinopsis:

Comprueba si son divisibles por 2, 3, 4, 5, 6, 10, 11 ó 12, los siguientes números: 405, 316, 814, 3080 y 240.

Ejercicio 2 (1'50") Sinopsis:

Escribe cuatro números de forma que sean divisibles a la vez entre 2 y 11.

Ejercicio 3 (9'07") Sinopsis:

Comprueba si son divisibles por 2, 3, 4, 5, 6, 9 ó 10, los siguientes números: 2 799 588, 5670 y 100 765.

Ejercicio 4 (7'46") Sinopsis:

Comprueba si 380 es divisible por 2, 3, 4, 5, 6, 9 ó 10.

Criterios de divisibilidad

Actividad 1 Descripción:

Actividad en la que podrás comprobar si un número dado es múltiplo o no de 2, 3, 4, 5, 6, 8, 9, 10 y 11.
Actividad en la que deberás separar los números por los que es divisible un número dado.

Actividad 2 Descripción:

Actividad 3 Descripción:

Actividad sobre criterios de divisibilidad por 2, 3, 5, 7, 9, 10 y 11.

Actividad 4a (divisibilidad por 2) Descripción:

Averigua los múltiplos de 2

Actividad 4b (divisibilidad por 3) Descripción:

Averigua los múltiplos de 3

Actividad 4c (divisibilidad por 5) Descripción:

Averigua los múltiplos de 5

Actividad 4d (divisibilidad por 11) Descripción:

Averigua los múltiplos de 11

Actividad 5 (divisibilidad por 2, 3 y 5) Descripción:

Averigua qué número no es múltiplo del dado.

Autoevaluación 1 Descripción:

Test de 5 preguntas sobre divisibilidad.

Autoevaluación 2 Descripción:

Test de 5 preguntas sobre divisibilidad.

Autoevaluación 3 Descripción:

Test de 7 preguntas sobre divisibilidad.

Autoevaluación 4 Descripción:

Criterios de divisibilidad del 2, 3, 5 y 11

Autoevaluación 5 Descripción:

Ejercicios de autoevaluación sobre criterios de divisibilidad.

Números compuestos y números primos

Plantilla:Números compuewstos y números primos

Descomposición factorial de un número

Cualquier número podemos expresarlo como producto de potencias de números primos. A esto se le llama descomposición factorial de un número.

Para descomponer en factores primos un número:

Lo dividimos por el primer número primo que podamos.
El cociente que haya resultado lo colocamos bajo el número.
Si podemos seguimos dividiendo sucesivamente ese cociente por el mismo número primo.
Cuando no podamos hacer la división por ese número primo lo hacemos por el siguiente primo que se pueda.
Así sucesivamente hasta que el cociente final sea 1.

Ejemplo: Descompoción en factores primos

Halla la descomposición factorial de 90.

Solución:

Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2.

90:2=45

A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma.

45:3=15

Así sucesivamente hasta obtener 1 en el cociente

15:3=5

5:5=1

Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90.

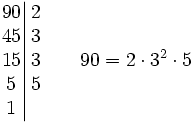
$\left . \begin{matrix} 90 \\ 45 \\ 15 \\ 5 \\ 1 \end{matrix} \right |\begin{matrix} 2 \\ 3 \\ 3 \\ 5 \\ \; \end{matrix} \qquad 90=2 \cdot3^2 \cdot 5$

Actividad Interactiva: Descomposición factorial de un número

1. Descompón un número en factores primos.

Actividad:

Esta escena realiza la descomposición factorial de un número, para ello marca el número natural que quieras en la ventana del control que está bajo la escena y pulsa intro. El número más grande que puedes marcar es de cinco cifras.

A la derecha puedes ver los factores que intervienen y abajo la expresión del producto de potencias. Si el exponente es 1 no se pone exponente.

Click aquí si no se ve bien la escena

Realiza en tu cuaderno y comprueba en la escena anterior la descomposición en factores de los números:

a) 700 b) 1024 c) 658

Obtención de los divisores de un número

Para obtener los divisores de un número podemos proceder siguiendo uno de los dos métodos que ilustramos con el siguiente ejemplo:

Ejemplo: Obtener los divisores de un número

Obtén los divisores de 90.

Solución:

Método 1: Descomponemos 90 en factores primos:

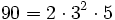
$90=2 \cdot3^2 \cdot 5$

Construimos una tabla para formar las posibles combinaciones de productos de factores.

Cada casilla de la tabla contiene un divisor: 1, 3, 9, 2, 6, 18, 5, 15, 45, 10, 30 y 90.

Método 2: Dividimos 90 por su primer divisor:

90:1=90. Ya tenemos dos divisores: 1 y 90.

Dividimos 90 por el siguiente divisor:

90:2=45. Ya tenemos otros dos: 2 y 45.

Proseguimos de igual forma:

90:3=30. Obtenemos 3 y 30.

90:5=18. Obtenemos 5 y 18.

90:6=15. Obtenemos 6 y 15.

90:9=10. Obtenemos 9 y 10.

Paramos porque el siguiente divisor es 10, que ya se ha obtenido.

Actividad Interactiva: Divisores de un número

1. Calcula los divisores de un número.

Actividad:

Marca el número que quieras en la ventana del control que está bajo la escena y pulsa intro, así aparecerán todos los divisores que tiene ese número.

También puedes ir variando el valor del número utilizando los triángulos arriba y abajo. El número más grande que puedes marcar es el 10.000

Click aquí si no se ve bien la escena

Investiga y contesta en tu cuaderno:

Toma nota de la cantidad de divisores de cada uno de los números del 0 al 50

a) ¿Cuál es el número natural que tiene mayor cantidad de divisores? ¿Cuántos divisores tiene?

b) ¿Cuál es el número natural que tiene menor cantidad de divisores? ¿Cuántos divisores tiene?

c) ¿Cuántos divisores tiene un número primo?

Marca un número de 4 cifras, pulsa intro, con el triángulo arriba vete aumentando de uno en uno el valor del número. Observa la disparidad de número de divisores que tiene cada número. Anota lo que observes.

d) ¿Crees que un número grande es de esperar necesariamente que tenga más divisores?

e) ¿De qué crees que depende?

Máximo común divisor

El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Para obtenerlo se descomponen los números en factores primos y se toman los factores comunes elevados al menor exponente.

Ejemplo: m.c.d.

Calcula el m.c.d.(24,60).

Solución:

Descomponemos 24 y 60 en sus factores primos:

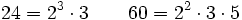
$24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5$

Multiplicando los factores comunes elevados al menor exponente:

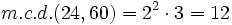
$m.c.d.(24,60)= 2^2 \cdot 3=12$

Actividad Interactiva: m.c.d.

1. Calcula el m.c.d. de dos números.

Actividad:

Calcula mentalmente y anota en tu cuaderno el máximo común divisor de estos dos números; márcalo en la ventana del control inferior y pulsa intro.

Si necesitas ayuda pulsa sobre los triángulos del control de arriba y verás la descomposición factorial de cada número, pero en ese caso el mensaje ENHORABUENA tendrá otro color.

Cada vez que pulses sobre "inicio" aparecerán otros dos números aleatoriamente.

Click aquí si no se ve bien la escena

Propiedad

Si a es múltiplo de b, entonces m.c.d.(a,b)=b.

Por ejemplo, m.c.d.(15, 30)=15.

Números primos entre sí

Dos números son primos entre sí, si su m.c.d. es 1.

Por ejemplo, 6 y 11 son primos entre sí.

Mínimo común múltiplo

El mínimo común múltiplo (m.c.m.) de dos o más números es el menor de todos los múltiplos comunes a esos números.
Para obtenerlo se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.

Ejemplo: m.c.m.

Calcula el m.c.m.(24,60).

Solución:

Descomponemos 24 y 60 en sus factores primos:

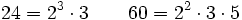
$24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5$

Multiplicando todos los factores elevados al mayor exponente:

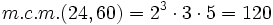
$m.c.m.(24,60)= 2^3 \cdot 3 \cdot 5=120$

Actividad Interactiva: m.c.m.

1. Calcula el m.c.m. de dos o tres números.

Actividad:

Calcula y anota en tu cuaderno el mínimo común múltiplo de estos números; márcalo en la ventana del control inferior y pulsa intro.

Si necesitas ayuda pulsa sobre los triángulos del control de arriba y verás la descomposición factorial de cada número, pero en ese caso el mensaje ENHORABUENA tendrá otro color.

Cada vez que pulses sobre "inicio" aparecerán otros dos números aleatoriamente.

Calcula el m.c.m. de dos números menores que 10:

Click aquí si no se ve bien la escena

Calcula el m.c.m. de dos números menores que 100:

Shift-Click aquí si no se ve bien la escena

Calcula el m.c.m. de tres números menores que 10:

Click aquí si no se ve bien la escena

Propiedades

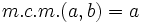Si a es múltiplo de b, entonces $m.c.m.(a,b)=a \;\!$ .
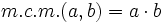Si a y b son primos entre sí, entonces $m.c.m.(a,b)=a \cdot b$ .

Por ejemplo:

m.c.m.(15, 30)=30, porque 30 es múltiplo de 15.
m.c.m.(4,11)=44, porque 4 y 11 son primos entre sí.

Actividad Interactiva: m.c.d. y m.c.m.

Actividad 1: Una fórmula que relaciona el m.c.d. y el m.c.m.

Actividad:

Click aquí si no se ve bien la escena

Ejercicios y problemas

Ejercicios

Actividad Interactiva: m.c.d. y m.c.m.

Actividad 1: Las baldosas de mi cuarto.

Actividad:

Click aquí si no se ve bien la escena

Ejercicios

1. Averigua si son primos o no los números 233 y 1.573.

Solución:

233 es primo.
1.573 es compuesto.

2. Descompón en factores los números 3.450 y 114.400.

Solución: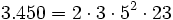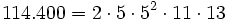

$3.450=2 \cdot 3 \cdot 5^2 \cdot 23$
$114.400=2 \cdot 5 \cdot 5^2 \cdot 11 \cdot 13$

3. Escribe todos los divisores de 840

Solución:

1, 2, 3, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70, 84, 105, 120, 140, 168, 210, 280, 420 y 840.

4. Halla el máximo común divisor y el mínimo común múltiplo de:

a) 55 y 35 b) 20, 40 y 60 c) 16 y 68 d) 12, 18 y 24.

Solución:

m.c.d.: a) 5 b) 20 c) 4 d) 6
m.c.m.: a) 385 b) 120 c) 272 d) 72

5. ¿Cuáles de estos pares de números son primos entre sí?

a) 84 y 41 b) 150 y 21 c) 200 y 131 d) 132 y 121.

Solución:

a), c) y d)

Problemas

Problemas

1. Cierto planeta A tarda 150 días en completar una orbita completa alrededor de su sol. Otro planeta B del mismo sistema solar lo hace en 225 días. Si cierto día ambos planetas están alineados con el sol, ¿Cuánto tardarán en volver a estarlo?

Solución:

450 años.

2. Jaime hace una revisión rutinaria de su vehículo cada 15.000 km y hace otra revisión más a fondo cada 70.000 km ¿Cada cuántos kilómetros coinciden las dos revisiones?

Solución:

210.000 km.

3. Una empresa vinícola de Montilla tiene que embasar 1.650 litros de vino dulce y 3.600 litros de vino fino, en toneles iguales de la mayor capacidad posible. ¿De qué capacidad serán los toneles?

Solución:

150 l.

4. Se desea cubrir con azulejos cuadrados una pared de una cocina que mide 210 cm de ancho por 300 cm de alto. Si queremos que los azulejos sean lo más grande posible y que no haya que romper ninguno, ¿cuál debe ser la anchura del azulejo?

Solución:

30 cm.

5. En una peña hay entre 300 y 400 amigos. Para hacer una competición podemos formar grupos de 9, de 15 o de 21, sin que sobre o falte nadie. ¿Cuántos son en la peña?

Solución:

315

6. Si agrupamos las cajas de una almacén de 2 en 2, de 3 en 3, o de 4 en 4, siempre sobra 1. Calcula cuántos cajas hay sabiendo que no hay más de 20.

Solución:

Calculadora

WIRIS: Factorizar, m.c.d., m.c.m., números primos

Ejemplos:

Click aquí si no se ve bien la escena

Ayúdate de los ejemplos anteriores y utiliza el editor para:

a) Calcular m.c.d.(24,68,80).

b) Calcular m.c.m.(12,16,20).

c) Descomponer en factores primos del número 2.560.

d) Comprobar si el número 331 es primo.

Hazlos primero en tu cuaderno.

Editor:

Click aquí si no se ve bien la escena

Obtenido de "http://maralboran.org/wikipedia/index.php/Divisibilidad"

Categorías: Matemáticas | Números

 {{p}}
 ==Números compuestos y números primos==
-{{Tabla75|
+{{Números compuewstos y números primos}}
-celda1=
-{{p}}{{Caja_Amarilla|texto=
-Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}}<br>
-Por ejemplo, 15 es compuesto porque <math>15=3 \cdot 5</math>. Sin embargo, los números 2, 3, 5, 7, 11, 13 son primos.<br>
-<br>
-{{Caja Amarilla|texto=
-'''Propiedad:''' Un número primo sólo tiene por divisores a la unidad y a él mismo.}}
-|celda2=
-[[Imagen:tabla_primos.png|center|thumb|Números primos menores que 100]]
-}}
 {{p}}
-{{Video2
-|titulo1=Números naturales. Números primos
-|duracion=17´
-|sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos
-números?...   Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.
-|url1=http://maralboran.org/web_ma/videos/naturales/naturales.htm
-}}
-{{p}}
-===Criba de Eratóstenes===
-La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C.
-<br>
-{{AI2|titulo=Actividad Interactiva: ''Criba de Eratóstenes''|cuerpo=
-{{ai_cuerpo
-|enunciado=1. Practica el algoritmo de la criba de Eratóstenes.
-|actividad=
-La Criba de Eratóstenes es un procedimiento para obtener los primeros números primos.
-* Se comienza con un panel en el que están colocados los números naturales a partir del número 2. Normalmente se hace con los cien primeros números naturales, aquí emplearemos solamente hasta el número 46.
-* Comenzamos por el número 2, lo dejamos, pero a partir de él contamos de 2 en 2 y eliminamos los números que sean múltiplos de 2.
-* El primer número de los que quedan es el 3, lo dejamos y desde el número 3 eliminamos los números que sean múltiplos de 3.
-* El siguiente número de los que quedan es el 5, lo dejamos y desde el número 5 eliminamos los números que sean múltiplos de 5.
-* Así vamos avanzando, cuando llegamos a un número que no ha sido eliminado lo dejamos, pero a partir de él eliminamos los números que sean múltiplos de él. Así hasta el final.
-* Finalmente habrán quedado solamente números primos.
-<center><iframe>
-url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/criba_1.html
-width=650
-height=470
-name=myframe
-</iframe></center>
-<center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/criba_1.html '''Click''' aquí si no se ve bien la escena]</center>
-}}
-}}
-{{p}}
-===Cómo averiguar si un número es primo===
-Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).
-{{Ejemplo
-|titulo=Ejemplo: ''Averiguar si un número es primo''
-|enunciado=
-:Averigua si el número 167 es primo.
-|sol=
-Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:<br>
-:Dividimos 167 entre 2: cociente=83 y resto=1. No es divisible por 2.
-:Dividimos 167 entre 3 porque 83>3: cociente=55 y resto=2. No es divisible por 3.
-:Dividimos 167 entre 5 porque 55>5: cociente=33 y resto=2. No es divisible por 5.
-:Dividimos 167 entre 7 porque 33>7: cociente=23 y resto=6. No es divisible por 7.
-:Dividimos 167 entre 11 porque 23>11: cociente=15 y resto=2. No es divisible por 11.
-:Dividimos 167 entre 13 porque 15>13: cociente=12 y resto=11. No es divisible por 13.
-:Paramos y no dividimos 167 entre 17 porque 12<17.<br>
-Por tanto, 167 es primo.
-}}
-{{p}}
-{{AI2|titulo=Actividad Interactiva: ''Números primos y compuestos''|cuerpo=
-{{ai_cuerpo
-|enunciado=1. Descubre si un número es primo o compuesto.
-|actividad=
-Marca el número que quieras en la ventana del control inferior y pulsa intro, después puedes ir variando el valor del número de uno en uno utilizando los triángulos arriba y abajo.
-El ordenador te indicará si ese número es primo o compuesto. En caso de ser compuesto te indicará además por qué número se le puede dividir después del 1.
-El número más grande que puedes marcar es el 10.000.000.000
-<center><iframe>
-url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/primos_1.html
-width=400
-height=420
-name=myframe
-</iframe></center>
-<center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/primos_1.html '''Click''' aquí si no se ve bien la escena]</center>
-'''Investiga y contesta en tu cuaderno:'''
-a) Desde el número 2, utilizando el triángulo arriba, aumenta de uno en uno y cuenta los números primos que hay en la primera centena desde el 2 hasta el 101.
-b) Marca después un número de 9 cifras, comienza con uno que termine en 00, aumenta de uno en uno y haz el recuento de los números primos que encuentres en esa centena.
-c) ¿Qué deduce?
-}}
-}}
-{{p}}
 ===Descomposición factorial de un número===
 {{Caja_Amarilla|texto=Cualquier número podemos expresarlo como producto de potencias de números primos. A esto se le llama '''descomposición factorial''' de un número.}}

Divisibilidad

De Wikipedia

Revisión de 07:35 20 feb 2009

Tabla de contenidos

Múltiplos y divisores

Criterios de divisibilidad

Números compuestos y números primos

Descomposición factorial de un número

Obtención de los divisores de un número

Máximo común divisor

Propiedad

Números primos entre sí

Mínimo común múltiplo

Propiedades

Ejercicios y problemas

Ejercicios

Problemas

Calculadora

Vistas

Herramientas personales

Menú

Buscar

Herramientas