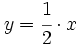Funciones lineales: Función de proporcionalidad directa
De Wikipedia
| Revisión de 06:19 15 abr 2009 Coordinador (Discusión | contribuciones) (→Función lineal de proporcionalidad directa) ← Ir a diferencia anterior |
Revisión de 12:05 15 abr 2009 Coordinador (Discusión | contribuciones) (→Función lineal de proporcionalidad directa) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| ==Función lineal de proporcionalidad directa== | ==Función lineal de proporcionalidad directa== | ||
| {{Caja_Amarilla|texto=Una '''función lineal de proporcionalidad directa''' es aquella cuya expresión matemática viene dada por: | {{Caja_Amarilla|texto=Una '''función lineal de proporcionalidad directa''' es aquella cuya expresión matemática viene dada por: | ||
| + | {{p}} | ||
| <center><math>y=m \cdot x</math></center> | <center><math>y=m \cdot x</math></center> | ||
| + | {{p}} | ||
| donde <math>x\;\!</math> e <math>y\;\!</math> son variables y <math>m\;\!</math> una constante que se denomina '''pendiente'''. Su gráfica es una recta que pasa por el origen.}} | donde <math>x\;\!</math> e <math>y\;\!</math> son variables y <math>m\;\!</math> una constante que se denomina '''pendiente'''. Su gráfica es una recta que pasa por el origen.}} | ||
| {{p}} | {{p}} | ||
Revisión de 12:05 15 abr 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Función de Prop. Directa (en Thales) Función de Prop. Directa (en Descartes) Funciones (SM) | Ejercicios Ecuación pto-pendiente Ecuaciones de la recta | WIRIS Geogebra Calculadora Función lineal Recta |
Función lineal de proporcionalidad directa
Una función lineal de proporcionalidad directa es aquella cuya expresión matemática viene dada por:
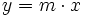
donde  e
e  son variables y
son variables y 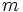 una constante que se denomina pendiente. Su gráfica es una recta que pasa por el origen.
una constante que se denomina pendiente. Su gráfica es una recta que pasa por el origen.
|
Actividades Interactivas: Función lineal de proporcionalidad directa
1. Ejemplos de funciones lineales de proporcionalidad directa.
Actividad:
La función En la siguiente escena, mueve el punto rojo y comprueba que todos los puntos de la recta cumplen la condición Como ves la representación gráfica de la función identidad es una recta, que es la bisectriz de los cuadrantes primero y tercero del sistema de referencia cartesiano. Todos los puntos de esa recta tienen sus coordenadas idénticas, para cada punto su abscisa es igual que su ordenada.
En la siguiente escena vamos a comparar las funciones a) Observa como la función Observa esta otra escena: b) Modifica el valor de m con los pulsadores o escribiendo el valor y pulsando "intro", para obtener las gráficas de las funciones c) Dibuja las anteriores funciones en tu cuaderno a partir de sus tablas de valores. d) ¿Qué tienen todas en común?
2. Significado de la pendiente.
Actividad: Observa la escena, mueve el punto rojo y responde a las preguntas: a) Explica qué significado tiene que la pendiente sea positiva o negativa. b) ¿Que tipo de recta obtienes cuando la pendiente es 0? c) ¿Qué ocurre con la recta vertical? ¿Qué pendiente tiene?
3. Averigua el valor de la pendiente.
Actividad: Consideremos la función 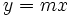 , cuya pendiente es , cuya pendiente es  . .
La pendiente de una recta tiene mucha relación con las coordenadas de los puntos por donde pasa. En la siguiente escena tienes que seleccionar el número que corresponde a la pendiente de la recta azul fijándote en las coordenadas del punto rojo de la recta. Para dar valores a |
Ejercicios
|
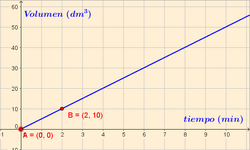
Ejercicio: Función lineal 1. Un grifo tiene un caudal de 5 dm3 por minuto.
|
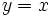 se denomina función identidad, porque a cada número del eje de abscisas le corresponde el mismo número en el eje de ordenadas, es decir, que las dos coordenadas de cada punto son idénticas (1,1), (2,2), etc.
se denomina función identidad, porque a cada número del eje de abscisas le corresponde el mismo número en el eje de ordenadas, es decir, que las dos coordenadas de cada punto son idénticas (1,1), (2,2), etc.
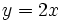 .
.
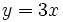 , e
, e