Ángulos en la circunferencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:43 19 dic 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:57 27 abr 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 30: | Línea 30: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | '''a)''' Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | + | '''a)''' Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.{{p}} |
| + | '''b)''' La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | ||
| {{Desplegable2 | {{Desplegable2 | ||
| |titulo=Demostración: | |titulo=Demostración: | ||
| - | |contenido=Mueve el vértice V y observa que no varía la medida del ángulo <math>\widehat{AVB}</math>. | + | |contenido=Arrastra los puntos A y B. |
| - | <center><iframe> | + | *Describe lo que observas: ¿qué relación hay entre las medidas de los tres ángulos destacados? |
| - | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_2.html | + | |
| - | width=380 | + | Cambia ahora la posición de P y Q |
| - | height=350 | + | |
| - | name=myframe | + | *¿Se sigue cumpliendo la relación? |
| - | </iframe></center> | + | |
| - | }} | + | Desliza el punto verde y describe lo que observes |
| - | '''b)''' La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | ||
| - | {{Desplegable2 | ||
| - | |titulo=Demostración: | ||
| - | |contenido=Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_3.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_1.html |
| - | width=380 | + | width=780 |
| - | height=350 | + | height=460 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
| + | |||
| '''c)''' Todo ángulo inscrito en una semicircunferncia es recto. | '''c)''' Todo ángulo inscrito en una semicircunferncia es recto. | ||
| {{Desplegable2 | {{Desplegable2 | ||
| |titulo=Demostración: | |titulo=Demostración: | ||
| - | |contenido=Sea AB un diámetro de la circunferencia: <math>\widehat{AOB}=180^o</math>. Por el apartado a), el ángulo inscrito <math>\widehat{AVB}=\cfrac{180^o}{2}=90^o</math>. | + | |contenido=Sea AB un diámetro de la circunferencia: {{sube|porcentaje=+20%|contenido=<math>\widehat{AOB}=180^o</math>}}. Por el apartado a), el ángulo inscrito <math>\widehat{AOB}=\cfrac{180^\circ}{2}=90^\circ</math>. |
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geometria/geoweb/circun4_4.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_2.html |
| - | width=420 | + | width=780 |
| - | height=350 | + | height=460 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | Observa y manipula la figura: | ||
| + | |||
| + | *¿Cuál es la posición del triángulo APB respecto de la semicircunferencia? | ||
| + | *¿Cuánto estimas que puede medir el ángulo en P? | ||
| + | |||
| + | Desliza el punto verde y observa. | ||
| + | |||
| + | *¿Qué relación hay entre el ángulo verde (APB) y el azul (AOB)? | ||
| + | *¿Cuál será la medida de cada uno de ellos? | ||
| + | *Como conclusión: ¿qué se puede decir de los ángulos inscritos en una semicircunferencia? | ||
| - | Mueve el vértice V y comprueba que el ángulo siempre es recto. Este resultado proporciona una excelente forma de construir ángulos rectos y triángulos rectángulos. | ||
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 06:57 27 abr 2009
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
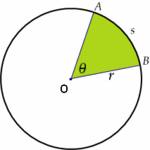
Ángulo central
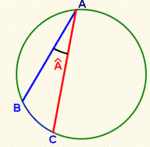
Ángulo inscrito
Propiedades
a) Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
b) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
Demostración:
Arrastra los puntos A y B.
- Describe lo que observas: ¿qué relación hay entre las medidas de los tres ángulos destacados?
Cambia ahora la posición de P y Q
- ¿Se sigue cumpliendo la relación?
Desliza el punto verde y describe lo que observes
c) Todo ángulo inscrito en una semicircunferncia es recto.
Demostración:
Sea AB un diámetro de la circunferencia: 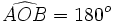 . Por el apartado a), el ángulo inscrito
. Por el apartado a), el ángulo inscrito 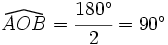 .
.
Observa y manipula la figura:
- ¿Cuál es la posición del triángulo APB respecto de la semicircunferencia?
- ¿Cuánto estimas que puede medir el ángulo en P?
Desliza el punto verde y observa.
- ¿Qué relación hay entre el ángulo verde (APB) y el azul (AOB)?
- ¿Cuál será la medida de cada uno de ellos?
- Como conclusión: ¿qué se puede decir de los ángulos inscritos en una semicircunferencia?
 y su arco correspondiente AB.
y su arco correspondiente AB.
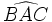 .
.