Números enteros: Potencias
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:54 23 nov 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:57 23 nov 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| |enlaces=[http://es.wikipedia.org/wiki/Numeros_enteros Números enteros]}}{{p}} | |enlaces=[http://es.wikipedia.org/wiki/Numeros_enteros Números enteros]}}{{p}} | ||
| ==Potencias de enteros== | ==Potencias de enteros== | ||
| - | Los enteros cumplen las mismas [http://maralboran.org/wikipedia/index.php/N%C3%BAmeros_naturales#Propiedades_de_las_potencias_de_naturales propiedades] de las potencias de los números naturales. Dependiendo del signo de la base tenemos estas dos posibilidades: | + | Dependiendo del signo de la base tenemos estas dos posibilidades: |
| {{p}} | {{p}} | ||
| {{Caja Amarilla|texto=*Si la base es '''positiva:''' Al elevar un número positivo a una potencia, el resultado es positivo. | {{Caja Amarilla|texto=*Si la base es '''positiva:''' Al elevar un número positivo a una potencia, el resultado es positivo. | ||
| Línea 44: | Línea 44: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Propiedades de las potencias de enteros== | ||
| + | Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales. | ||
| + | {{p}} | ||
| + | {{Caja Amarilla|texto=<center><math>a^0=1\,\!</math>{{b}}{{b}}<math>a^m \cdot a^n=a^{n+m}</math>{{b}}{{b}}<math>\cfrac{a^m}{a^n}=a^{m-n}\,\!</math>{{b}}{{b}}<math>(a^m)^n=a^{m \cdot n}</math> | ||
| + | </center> | ||
| + | {{p}} | ||
| + | <center><math>(a^n \cdot b^n)=(a \cdot b)^n</math>{{b}}{{b}}<math>\cfrac{a^n}{b^n}=\left ( \frac{a}{b} \right )^n\,\!</math> | ||
| + | </center> | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios: ''Potencias de enteros'' | |titulo=Ejercicios: ''Potencias de enteros'' | ||
Revisión de 11:57 23 nov 2009
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Números enteros I | WIRIS Geogebra Calculadora Números enteros |
Potencias de enteros
Dependiendo del signo de la base tenemos estas dos posibilidades:
- Si la base es positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Si la base es negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Ejemplos:
|
Actividad Interactiva: Potencias de números enteros
Actividad 1. Potencias de base negativa.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. |
Propiedades de las potencias de enteros
Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales.
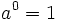
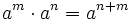
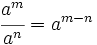
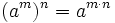
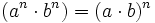
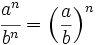
|
Ejercicios: Potencias de enteros 1. Calcula:
Solución: a) -8 b) -16 c) 64 d) 1 e) -1 f) -1 |
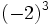 b)
b) 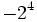 c)
c) 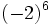 d)
d) 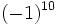 e)
e) 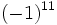 f)
f)