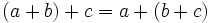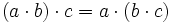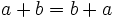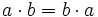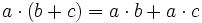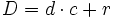Números naturales
De Wikipedia
| Revisión de 09:59 15 abr 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 14:17 15 abr 2007 Coordinador (Discusión | contribuciones) (→Jerarquía de las operaciones) Ir a siguiente diferencia → |
||
| Línea 59: | Línea 59: | ||
| {{p}} | {{p}} | ||
| ===Jerarquía de las operaciones=== | ===Jerarquía de las operaciones=== | ||
| - | A la hora de operar con números seguiremos las siguientes pautas: | + | A la hora de operar con números naturales seguiremos las siguientes pautas: |
| {{Caja Amarilla|texto=Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. | {{Caja Amarilla|texto=Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. | ||
| Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | ||
| Línea 68: | Línea 68: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ejercicios y problemas== | ==Ejercicios y problemas== | ||
| ===Ejercicios=== | ===Ejercicios=== | ||
Revisión de 14:17 15 abr 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar | Números naturales Aritmética | WIRIS Geogebra Calculadora {{{enlaces}}} |
Tabla de contenidos |
Definición
El conjunto de los números naturales es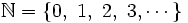 
. Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Podemos representarlos en una recta:
Operaciones
Suma y multiplicación
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Resta y división
La resta (o substracción)y la división (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición externa.
Propiedades
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
División
La división puede verse como un reparto de un número de elementos (dividendo) en un número de partes iguales (divisor), que da como resultado el número de elementos que corresponden a cada parte (cociente) y un posible número de elementos sobrantes (resto). Si el resto es cero la división se llama exacta, si no, se llama entera.
Regla de la división: En toda división, el dividendo es igual al divisor por el cociente más el resto.
|
|
donde D es el dividendo, d el divisor, c el cociente y r el resto.
Potenciación
Una potencia de base a y exponente n consiste en multiplicar n veces la base a.
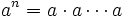
Propiedades:
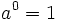
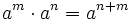
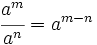
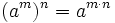
Actividades Interactivas: Potencia de exponente natural
Jerarquía de las operaciones
A la hora de operar con números naturales seguiremos las siguientes pautas:
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
