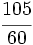Números racionales: Definición
De Wikipedia
| Revisión de 19:05 3 sep 2016 Coordinador (Discusión | contribuciones) (→Fracciones propias e impropias) ← Ir a diferencia anterior |
Revisión de 19:12 3 sep 2016 Coordinador (Discusión | contribuciones) (→Fracciones propias e impropias) Ir a siguiente diferencia → |
||
| Línea 84: | Línea 84: | ||
| ==Fracciones propias e impropias== | ==Fracciones propias e impropias== | ||
| - | {{Caja Amarilla|texto='''Fracciones propias''' son aquellas cuyo numerador es menor que el denominador. Son menores que 1.<br> '''Fracciones impropias''' son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1.}} | + | {{Caja Amarilla|texto=*'''Fracciones propias''' son aquellas cuyo numerador es menor que el denominador. Son menores que 1. |
| + | *'''Fracciones impropias''' son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{AI2|titulo=Actividades Interactivas: ''Fracciones propias e impropias''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Fracciones propias e impropias''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Separa las fracciones propias de las impropias. | + | |enunciado={{b4}}Separa las fracciones propias de las impropias. |
| |actividad= | |actividad= | ||
| Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. | Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. | ||
| Línea 111: | Línea 113: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Caja Amarilla|texto=*Una fracción se dice que está en '''forma mixta''' si está expreada com suma de un entero y una fracción propia.}} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Proposición: ''Transformar una fración impropia a forma mixta'' | + | {{Teorema|titulo=Proposición: ''Expresar una fración impropia en forma mixta'' |
| |enunciado= | |enunciado= | ||
| - | :Toda fracción impropia se puede escribir en forma mixta (un entero más una fracción propia): | + | :Toda fracción impropia se puede escribir en forma mixta: |
| <center><math>\cfrac{D}{d}=c+\cfrac{r}{d}</math></center> | <center><math>\cfrac{D}{d}=c+\cfrac{r}{d}</math></center> | ||
Revisión de 19:12 3 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Fracciones IV | Fracciones | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Fracciones y números racionales
Los números enteros son útiles para contar u ordenar objetos, pero hay veces en las que es necesario dividir la unidad en partes iguales para poder expresar una medida: la mitad, la tercera parte, etc. Estas medidas se expresan por medio de fracciones.- Una fracción se expresa de la forma
 con
con 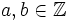 , donde
, donde  se llama numerador y
se llama numerador y  denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos. El valor de una fracción es el resultado de dividir numerador entre denominador.
denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos. El valor de una fracción es el resultado de dividir numerador entre denominador.
- Al conjunto de todas las fracciones también se le llama conjunto de números racionales. Lo representaremos por
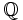 .
.
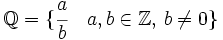
Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales.
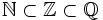 |
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Representación de fracciones en la recta numérica
|
Actividades Interactivas: Representación de fracciones en la recta numérica Actividad 1: Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica: a)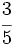 b) b) 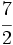 c) c)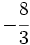 d) d) 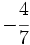 e) e) 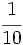 f) f) 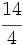 Actividad:
|
|
Actividad: Representación de fracciones en la recta numérica
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Fracciones propias e impropias
- Fracciones propias son aquellas cuyo numerador es menor que el denominador. Son menores que 1.
- Fracciones impropias son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1.
|
Actividades Interactivas: Fracciones propias e impropias
Separa las fracciones propias de las impropias.
Actividad: Puesto que una fracción representa una división, para saber cuál es el valor de una fracción deberíamos realizar esa división, no obstante, podemos apreciar el valor de una fracción si nos fijamos en su numerador y su denominador. Su valor será más grande cuanto mayor tenga el numerador, y será más pequeño cuanto mayor tenga el denominador.
Coloca cada fracción en el rectángulo que le corresponda según su valor. Pulsa "inicio" para que aparezcan otras fracciones. |
- Una fracción se dice que está en forma mixta si está expreada com suma de un entero y una fracción propia.
Proposición: Expresar una fración impropia en forma mixta
- Toda fracción impropia se puede escribir en forma mixta:
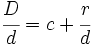
- donde
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
Ejemplo: Fracciones impropias
- Descompón la frácción impropia
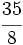 en la suma de un entero y una fracción propia (forma mixta).
en la suma de un entero y una fracción propia (forma mixta).
Dividimos 35 entre 8: 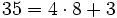
El dividendo 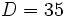 , el divisor
, el divisor 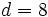 , el cociente
, el cociente 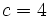 y el resto
y el resto 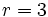 .
.
Aplicando la proposición anterior:
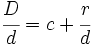
y sustituyendo cada letra por su valor:
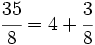
|
Calculadora: Fracciones impropias |
|
Actividad: Expresar fracciones en forma mixta
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Fracciones equivalentes
Fracciones equivalentes son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.
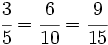
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
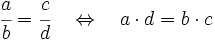
|
Actividades Interactivas: Fracciones equivalentes
Actividad 1: Busca una fracción equivalente a la dada.
Actividad: En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. Pulsa "inicio" para que aparezca otra fracción.
Actividad 2: Comprueba si dos fracciones son equivalentes o no (Método de los productos cruzados).
Actividad: Para comprobar si dos fracciones son equivalentes o no, el método más fácil es el de los productos cruzados. Multiplicamos sus términos en aspa. El producto del numerador de una fracción por el denominador de la otra ha de dar lo mismo en ambos casos. En la siguiente escena, escribe el numerador y denominador de otra fracción equivalente a ella y pulsa "intro" o usa los pulsadores. Después, pulsa sobre el triángulo azul para ver paso a paso la comprobación. Pulsa "inicio" para que aparezca otra fracción.
Actividad 3: Junta las fracciones equivalentes.
Actividad: Cada fracción de abajo es equivalente a otra de arriba. Colócala junto a ella. Para ello puedes buscar la fracción irreducible de cada una, o comprobar los productos cruzados de ambas. Pulsa "inicio" para que aparezcan otras fracciones. |
|
Actividad: Fracciones equivalentes
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debemos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción obtenida se dice que es irreducible.
|
Actividades Interactivas: Simplificación de fracciones
Actividad 1: Simplifica las fracciones.
Actividad: Todas las fracciones equivalentes entre sí representan el mismo número racional. Por tanto, para expresar un mismo valor nos interesa emplear la fracción más simple, ésa será la que tenga el numerador y denominador más pequeños. A esa fracción se la llama fracción irreducible porque ya no se la puede simplificar más. Nos valemos de la propiedad fundamental de la división. Sabemos que si multiplicamos o dividimos al numerador y al denominador por el mismo número obtenemos otra fracción equivalente. Para simplificar una fracción debemos buscar un número que sea divisor del numerador y del denominador para dividirlos por él. Nos interesa dividirlos por el número mayor posible, ese número es el máximo común divisor de ambos, así, de una sola vez habremos llegado a la fracción irreducible.
En esta escena aparece aleatoriamente una fracción, además se indican los divisores comunes del numerador y del denominador. Abajo debes marcar el número por el que dividirías al numerador y denominador para simplificar esa fracción. Pulsa "inicio" para que aparezca otra fracción.
Esta actividad es semejante a la anterior, pero en ésta no se da ayuda. Busca un número por el que puedes simplificar esta fracción, márcalo abajo y pulsa intro. Te indicará si con ello has llagado a la fracción irreducible o si todavía puedes seguir simplificando. En ese caso marca otro número. Tienes tres intentos para llegar a la fracción irreducible, pero no puedes rectificar, por eso no utilices los triángulos para cambiar los números marcados. Si la primera fracción es ya irreducible, marca el 1. Pulsa "inicio" para que aparezca otra fracción.
Actividad 2: Coloca junto a cada fracción su fracción irreducible.
Actividad:
Las fracciones de abajo son las irreducibles de las fracciones de arriba. Colócalas juntas. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta dos cifras. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta tres cifras. Pulsa "inicio" para que aparezcan otras fracciones. |
|
Actividad: Simplicar fracciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Orden en el conjunto de los racionales
De dos fracciones con el mismo denominador, es mayor la de mayor numerador. Por eso, para ordenar fracciones, debemos primero obtener fracciones equivalentes a las dadas, pero con el mismo denominador. A ésto se le llama reducir a común denominador. Veamos un ejemplo:
Ejemplo: Ordenar fracciones
- Ordena las fracciones:
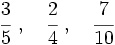
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
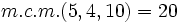 .
.Obtenemos fracciones equivalentes a las dadas con denominador 20. Para ello dividimos 20 entre cada denominador y lo multiplicamos por el numerador. Las fracciones obtenidas son:
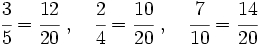
Estas fracciones las podemos ordenar fácilmente porque tienen el mismo denominador:
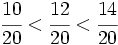
Así obtenemos:
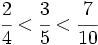
|
Actividad Interactiva: Ordenar fracciones
Actividad 1: Ordena de menor a mayor estas fracciones.
Actividad: Coloca estas fracciones ordenadas de menor a mayor. Pulsa "inicio" para que aparezcan otras fracciones. |
|
Actividad: Ordenar fracciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
|
Ejercicios: Fracciones equivalentes 1. Agrupa las fracciones que sean equivalentes: Solución: 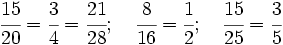 2. Simplifica las fracciones:
Solución: a) 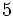 b) b) 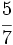 c) c) 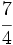 |
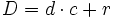
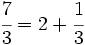
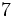

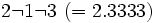
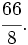
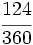 y
y 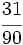 ?
?
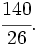
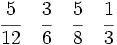
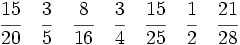
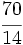 b)
b)  c)
c)