Problemas clásicos (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:06 13 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:14 13 sep 2016 Coordinador (Discusión | contribuciones) (→Repartos proporcionales) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 47) | (Pág. 47) | ||
| ==Repartos proporcionales== | ==Repartos proporcionales== | ||
| + | {{Caja_Amarilla|texto=En los '''repartos proporcionales''' tenemos que repartir una cantidad en varias partes, de manera que cada parte sea proporcional a cada fracción en que se parte el total.}} | ||
| + | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| |titulo=Ejercicio resuelto: ''Repartos proporcionales'' | |titulo=Ejercicio resuelto: ''Repartos proporcionales'' | ||
| - | |enunciado= | + | |enunciado={{p}} |
| + | :Tres grifos aportan 2 l/s, 5 l/s y 7l/s, respectivamente. Se abren los tres simultaneamente para llenar una balsa de 17080 l. Cuando la balsa está llena, ¿qué volumen de agua habrá manado de cada grifo? | ||
| {{p}} | {{p}} | ||
| - | |sol=}} | + | |sol= |
| + | :Los tres grifos aportan <math> 2+5+7=14 \ l/s</math>, de manera que: | ||
| + | |||
| + | :El primero aporta <math>\cfrac{2}{14}\;</math> del total <math>\rightarrow \cfrac{2}{14} \cdot 17080 = 2440 \ l</math> | ||
| + | |||
| + | :El segundo aporta <math>\cfrac{5}{14}\;</math> del total <math>\rightarrow \cfrac{5}{14} \cdot 17080 = 6100 \ l</math> | ||
| + | |||
| + | :El tercero aporta <math>\cfrac{7}{14}\;</math> del total <math>\rightarrow \cfrac{7}{14} \cdot 17080 = 8540 \ l</math> | ||
| + | |||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 26: | Línea 38: | ||
| {{p}} | {{p}} | ||
| (Pág. 48) | (Pág. 48) | ||
| + | |||
| ==Mezclas== | ==Mezclas== | ||
| {{Ejemplo | {{Ejemplo | ||
Revisión de 17:14 13 sep 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 47)
Repartos proporcionales
En los repartos proporcionales tenemos que repartir una cantidad en varias partes, de manera que cada parte sea proporcional a cada fracción en que se parte el total.
Ejercicio resuelto: Repartos proporcionales
- Tres grifos aportan 2 l/s, 5 l/s y 7l/s, respectivamente. Se abren los tres simultaneamente para llenar una balsa de 17080 l. Cuando la balsa está llena, ¿qué volumen de agua habrá manado de cada grifo?
Solución:
- Los tres grifos aportan
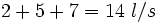, de manera que:
- El primero aporta
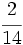del total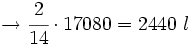 
- El segundo aporta
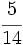del total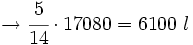 
- El tercero aporta
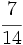del total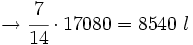 
 Ejercicios propuestos: Repartos proporcionales (Pág. 47) |
(Pág. 48)
Mezclas
Ejercicio resuelto: Mezclas
Solución:
Ejercicios propuestos: Mezclas (Pág. 49) |
(Pág. 49)
Móviles
Ejercicio resuelto: Móviles
Solución:
Ejercicios propuestos: Móviles (Pág. 49) |
