Números racionales

De Wikipedia

(Diferencia entre revisiones)

Revisión de 21:03 23 abr 2007

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Fracciones I Fracciones II Fracciones III Números decimales	Fracciones	WIRIS Geogebra Calculadora {{{enlaces}}}

Tabla de contenidos

1 Definiciones
2 Orden
3 Operaciones con fracciones
4 Expresión decimal de una fracción
- 4.1 Paso de fracción a decimal
- 4.2 Paso de decimal a fracción
5 Ejercicios y problemas
- 5.1 Ejercicios

Definiciones

Fracciones o números racionales

Así como los números naturales surgen para expresar cantidades que se refieren a objetos enteros, las fracciones son consecuencia de expresar cantidades que se refieren a partes de un objeto.

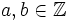Una fracción se expresa de la forma $\cfrac {a}{b}$ con $a,b \in \mathbb{Z}$ , donde $a\;\!$ se llama numerador y $b\;\!$ denominador. El denominador indica las partes iguales en que se divide a la unidad y el numerador las partes que tomamos.

El valor de una fracción es el resultado de dividir numerador entre denominador.

Al conjunto de todas las fracciones también se le llama conjunto de números racionales. Lo representaremos por 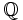$\mathbb{Q}$ .

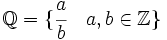
$\mathbb{Q} = \lbrace \cfrac {a}{b}\quad a,b \in \mathbb{Z} \rbrace$

Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales.

$\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}$

Actividades Interactivas: Fracciones

Fracciones propias e impropias

Fracciones propias son aquellas cuyo numerador es menor que el denominador. Son menores que 1.
Fracciones impropias son aquellas cuyo numerador es mayor o igual que el denominador. Son mayores que 1.

Actividades Interactivas: Fracciones propias e impropias

Fracciones equivalentes

Fracciones equivalentes son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.

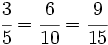
Cada fracción tiene infinitas fracciones equivalentes a ella. Podemos obtenerlas multiplicando numerador y denominador por un mismo número. Por ejemplo, $\cfrac{3}{5}=\cfrac{6}{10}=\cfrac{9}{15}$

Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.

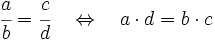
$\cfrac{a}{b}=\cfrac{c}{d} \quad\Leftrightarrow\quad a \cdot d=b \cdot c$

Si multiplicamos o dividimos el numerador y denominador por un mismo número, se obtienen fracciones equivalentes.

Actividades Interactivas: Fracciones equivalentes

Simplificar fracciones. Fracciones irreducibles

Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debemos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción obtenida se dice que es irreducible.

Actividades Interactivas: Simplificar de fracciones

Orden

De dos fracciones con el mismo denominador, es mayor la de mayor numerador. Por eso, para ordenar fracciones, debemos primero obtener fracciones equivalentes a las dadas, pero con el mismo denominador. A ésto se le llama reducir a común denominador. Veamos un ejemplo:

Ejemplo: Ordenar fracciones

Ordena las fracciones:

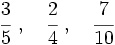
$\cfrac{3}{5}\ ,\quad \cfrac{2}{4}\ ,\quad\cfrac{7}{10}$

Solución:

Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:

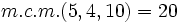$m.c.m.(5, 4, 10)=20\;\!$ .

Obtenemos fracciones equivalentes a las dadas con denominador 20. Para ello dividimos 20 entre cada denominador y lo multiplicamos por el numerador. Las fracciones obtenidas son:

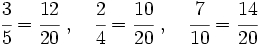
$\cfrac{3}{5}=\cfrac{12}{20}\ ,\quad\cfrac{2}{4}=\cfrac{10}{20}\ ,\quad\cfrac{7}{10}=\cfrac{14}{20}$

Estas fracciones las podemos ordenar fácilmente porque tienen el mismo denominador:

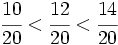
$\cfrac{10}{20}<\cfrac{12}{20}<\cfrac{14}{20}$

Así obtenemos:

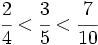
$\cfrac{2}{4}<\cfrac{3}{5}<\cfrac{7}{10}$

Actividad Interactiva: Ordenar fracciones

Ordena de menor a mayor

Operaciones con fracciones

Suma y resta

Para sumar o restar fracciones:

Si las fracciones tienen el mismo denominador, se suman o restan los numeradores y se pone el mismo denominador.
Si tienen distintos denominadores, primero se reducen a común denominador y luego se procede como en el caso anterior.

Ejemplo: Suma y resta de fracciones

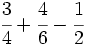
Calcula: $\cfrac{3}{4} + \cfrac{4}{6} - \cfrac{1}{2}$

Solución:

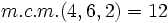Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores: $m.c.m.(4, 6, 2)=12\;\!$ .

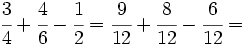
$\cfrac{3}{4} + \cfrac{4}{6} - \cfrac{1}{2}=\cfrac{9}{12} + \cfrac{8}{12} - \cfrac{6}{12}=$

Luego sumamos o restamos los númeradores, dejando el mismo denominador:

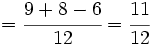
$=\cfrac{9+8-6}{12}=\cfrac{11}{12}$

Actividades Interactivas: Suma y resta de fracciones

Multiplicación

Para multiplicar fracciones, se pone como numerador, el producro de los numeradores, y como denominador, el producto de los denominadores.

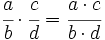
$\cfrac{a}{b} \cdot \cfrac{c}{d}=\cfrac{a \cdot c}{b \cdot d}$

No obstante, es conveniente simplificar los numeradores entre los denominadores antes de efectuar los productos.

Ejemplo: Producto de fracciones

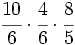
Calcula: $\cfrac{10}{6} \cdot \cfrac{4}{6} \cdot \cfrac{8}{5}$

Solución:

Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto:

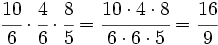
$\cfrac{10}{6} \cdot \cfrac{4}{6} \cdot \cfrac{8}{5}=\cfrac{10\cdot4\cdot8}{6\cdot6\cdot5}=\cfrac{16}{9}$

Actividades Interactivas: Multiplicación de fracciones

Inversa

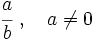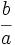Dada una fracción $\cfrac {a}{b}\ ,\quad a \ne 0$ , su inversa es la fracción $\cfrac {b}{a}$ .

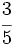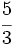Por ejemplo, la inversa de $\cfrac {3}{5}$ es $\cfrac {5}{3}$ .

Actividad Interactiva: Fracción inversa

Halla la fracción inversa

División

Para dividir dos fracciones, se pone como numerador, el producro del primer numerador por el segundo denominador, y como denominador, el producto del primer denominador por el segundo numerador.

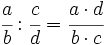
$\cfrac{a}{b} : \cfrac{c}{d}=\cfrac{a \cdot d}{b \cdot c}$

No obstante, es conveniente simplificar antes de efectuar los productos.

Ejemplo: Cociente de fracciones

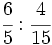
Calcula: $\cfrac{6}{5} : \cfrac{4}{15}$

Solución:

Multiplicamos en cruz, simplificando antes de efectuar el producto:

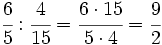
$\cfrac{6}{5} : \cfrac{4}{15}=\cfrac{6 \cdot 15}{5 \cdot 4}= \cfrac{9}{2}$

Actividad Interactiva: División de fracciones

Aprende a dividir fracciones

Potenciación

Las potencias con números racionales cumplen las mismas propiedades que con números naturales y enteros. Tan sólo mencionar el siguiente caso:

Potencias de exponente negativo

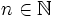Sea $n \in \mathbb{N}$ , se define: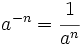

$a^{-n}=\cfrac{1}{a^n}$

Como consecuencia, 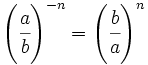$\left ( \cfrac{a}{b} \right )^{-n}=\left ( \cfrac{b}{a} \right )^{n}$ .

Expresión decimal de una fracción

Paso de fracción a decimal

Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:

Expresión decimal exacta: Si tiene un número finito de decimales.

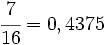Por ejemplo: $\cfrac{7}{16}=0,4375$ .

Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.

Por ejemplo: 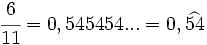$\cfrac{6}{11}=0,545454...=0,\widehat{54}$ . El periodo es 54.

Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.

Por ejemplo: 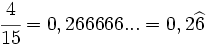$\cfrac{4}{15}=0,266666...=0,2\widehat{6}$ . El periodo es 6 y el anteperiodo 2.

Paso de decimal a fracción

Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:

Decimales exactos: Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.

Ejemplo: 34,65=3465/100

Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo.

Ejemplo: 15,3434...=(1534-15)/99

Decimales periódicos mixtos: Tendrá como numerador la diferencia entre a y b, donde a es el número escrito sin la coma, y b es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya.

Ejemplo: Sea el número 12,345 67 67... entonces a=1234567 y b=12345, por lo que el número buscado será (1234567-12345)/99000.

Veamos unos ejemplos que ilustren el porqué de tales procedimientos:

Ejemplo: Paso de decimal a fracción

Expresa en forma de fracción los números decimales:

a) 34,65 b) 15,34 34 c) 12,3 45 45

Solución:

Ejercicios y problemas

Ejercicios

Plantilla:Ejercicio cab

Obtenido de "http://maralboran.org/wikipedia/index.php/N%C3%BAmeros_racionales"

 ===Paso de decimal a fracción===
+Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:
+{{Caja Amarilla|texto=
+*'''Decimales exactos''': Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
+:Ejemplo: 34,65=3465/100
+*'''Decimales periódicos puros''': La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo.
+:Ejemplo: 15,3434...=(1534-15)/99
+*'''Decimales periódicos mixtos''': Tendrá como numerador la diferencia entre ''a'' y ''b'', donde ''a'' es el número escrito sin la coma, y ''b'' es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya.
+:Ejemplo: Sea el número 12,345 67 67... entonces ''a''=1234567 y ''b''=12345, por lo que el número buscado será (1234567-12345)/99000.
+}}{{p}}
+Veamos unos ejemplos que ilustren el porqué de tales procedimientos:
+{{Ejemplo
+|titulo=Ejemplo: ''Paso de decimal a fracción''
+|enunciado=
+:Expresa en forma de fracción los números decimales:
+::a) 34,65{{b}} b) 15,34 34{{b}} c) 12,3 45 45
+|sol=
+}}
+{{p}}
 ==Ejercicios y problemas==
 ===Ejercicios===

Números racionales

De Wikipedia

Revisión de 21:03 23 abr 2007

Tabla de contenidos

Definiciones

Fracciones o números racionales

Fracciones propias e impropias

Fracciones equivalentes

Simplificar fracciones. Fracciones irreducibles

Orden

Operaciones con fracciones

Suma y resta

Multiplicación

Inversa

División

Potenciación

Potencias de exponente negativo

Expresión decimal de una fracción

Paso de fracción a decimal

Paso de decimal a fracción

Ejercicios y problemas

Ejercicios

Vistas

Herramientas personales

Menú

Buscar

Herramientas