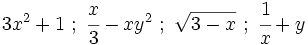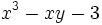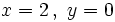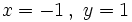Expresiones algebraicas
De Wikipedia
| Revisión de 16:31 24 oct 2016 Coordinador (Discusión | contribuciones) (→Valor numérico de una expresión algebraica) ← Ir a diferencia anterior |
Revisión de 16:32 24 oct 2016 Coordinador (Discusión | contribuciones) (→Tipos de expresiones algebraicas) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| {{p}} | {{p}} | ||
| ===Tipos de expresiones algebraicas=== | ===Tipos de expresiones algebraicas=== | ||
| - | Hay distintos tipos de expresiones algebraicas. | + | {{tipos de expresiones algebraicas}} |
| - | {{Caja_Amarilla|texto= | + | |
| - | *Dependiendo del número de sumandos, tenemos: '''monomios''' (1 sumando) y '''polinomios''' (varios sumandos). | + | |
| - | *Algunos polinomios tienen nombre propio: '''binomio''' (2 sumandos), '''trinomio''' (3 sumandos), ... | + | |
| - | *Dos expresiones algebraicas separadas por un signo <math>=\;\!</math> reciben el nombre de '''ecuación'''. | + | |
| - | *Un caso particular de ecuación es la '''identidad''', en la que los dos lados de la igualdad son equivalentes. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | *'''Monomios:''' <math>3x^5 \, ,\quad \cfrac{3x}{5} \, , \quad \cfrac{4}{3} \, \pi r^3</math> | + | |
| - | *'''Polinomios:''' <math>3x^5+2x\;\!</math> (binomio), <math>4ab-5b^2+ \cfrac{x}{5}</math> (trinomio) | + | |
| - | *'''Ecuaciones:''' <math>5x+3=2x-1\;\!</math> | + | |
| - | *'''Identidades:''' <math>(a+b)^2=a^2+2ab+b^2\;\!</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión de 16:32 24 oct 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Algebra (1º ESO) | WIRIS Geogebra Calculadora |
Expresiones algebraicas
- Una expresión algebraica es una combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...), que respeta las reglas del lenguaje algebraico.
- Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan variables. Los números se denominan constantes porque tienen un valor fijo.
- Se puede usar cualquier letra del alfabeto para expresar una variable, excepto la "e" y la "i", porque están reservadas para unos números especiales. Las letras más habituales son x, y, z, a, b, c, ...
- Las reglas que se mencionan en la definición son las mismas que ya teníamos en cuenta al trabajar únicamente con números y alguna otra que aparecerá más adelante. Entre ellas tenemos:
- Dos símbolos de operación no pueden aparecer juntos sin estar separados por otro elemento (paréntesis, corchetes, raya de fracción...)
- Cuando realizamos una operación combinada en varias etapas, cada una de ellas tiene que estar precedida del símbolo =, y los elementos que no se operan deben repetirse en la misma posición o en una equivalente, siempre respetando las propiedades de las operaciones.
- Si el símbolo = está seguido por una raya de fracción, ésta debe aparecer a una altura intermedia entre las dos rayas del igual.
- El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente.
- El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras).
- ...
Expresiones algebraicas: definición y ejemplos.
Expresiones algebraicas. Tipos de expresiones algebraicas: enteras y fraccionarias.
Indica si las siguientes expresiones algebraicas son enteras o fraccionarias:
- 44)
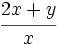 ; 45)
; 45) 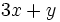 ; 46)
; 46) 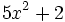
- 47)
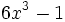 ; 48)
; 48) 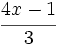 ; 49)
; 49) 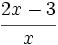
- 50)
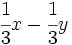
Ejemplos de expresiones algebraicas.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Tipos de expresiones algebraicas
Hay distintos tipos de expresiones algebraicas. Nosotros nos vamos a centrar, de manera especial, en unas que llamaremos monomios y polinomios.
- Monomio: es una expresión algebraica que consta de un número (coeficiente), multiplicado por letras (variables) con exponentes naturales.
- Polinomio: es la suma de varios monomios. Algunos polinomios tienen nombre propio: binomio (2 sumandos), trinomio (3 sumandos), ...
En general, cuando hablemos de polinomios, nos referiremos tanto a los monomios como a los polinomios. Es decir, un monomio lo veremos como un polinomio con un solo sumando.
- Monomios:
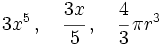
- Polinomios:
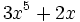 (binomio)
(binomio)
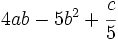 (trinomio)
(trinomio)
- No son monomios, ni polinomios:
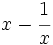 , porque la variable aparece dividiendo.
, porque la variable aparece dividiendo.
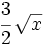 , porque la variable aparece dentro de una raíz.
, porque la variable aparece dentro de una raíz.
Elementos que componen una término algebraico.
Elementos que componen una expresión algebraica. Clasificación de las expresiones algebraicas.
Monomios, binomios, trinomios y polinomios. Ejemplos.
Actividad en la que deberás decir de qué tipo es la expresión algebraica dada.
Valor numérico de una expresión algebraica
Si en una expresión algebraica se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico de la expresión algebraica para los valores de las letras dados.
Ejemplo: Valor numérico de una expresión algebraica
Halla el valor numérico de los polinomios:
- a)
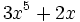 para
para 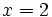
- b)
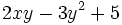 para
para 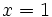 e
e 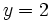 .
.
a) El valor numérico del polinomio es: 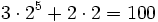
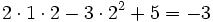
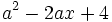 en los casos:
en los casos:
a) 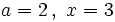
b) 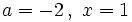
2. Encuentra algún valor de  y
y  que hagan que el valor numérico valga cero.
que hagan que el valor numérico valga cero.
Haz uso de la siguiente escena para comprobar los resultados: