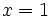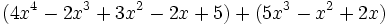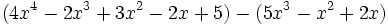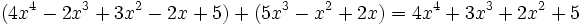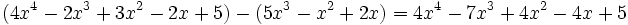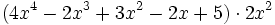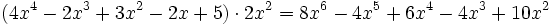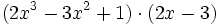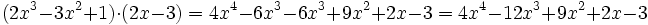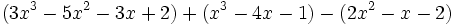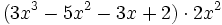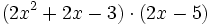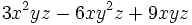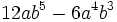Polinomios
De Wikipedia
| Revisión de 13:24 25 oct 2016 Coordinador (Discusión | contribuciones) (→Valor numérico de un polinomio) ← Ir a diferencia anterior |
Revisión de 13:25 25 oct 2016 Coordinador (Discusión | contribuciones) (→Valor numérico de un polinomio) Ir a siguiente diferencia → |
||
| Línea 37: | Línea 37: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | :Calcula el valor numérico del polinomio <math>x^2-3x+2\;\!</math> en los casos: | + | Calcula el valor numérico del polinomio <math>x^2-3x+2\;\!</math> en los casos: |
| :a) <math>x=2\!</math>{{b4}} b) <math>x=-2\!</math>{{b4}} c) <math>x=1\!</math> | :a) <math>x=2\!</math>{{b4}} b) <math>x=-2\!</math>{{b4}} c) <math>x=1\!</math> | ||
Revisión de 13:25 25 oct 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Algebra (1º ESO) | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Polinomios
- Un polinomio es una expresión algebraica que se obtiene al sumar dos o más monomios. A cada monomio se le llama término del polinomio. Si tiene dos términos se llama binomio; si tiene tres trinomio, etc.
- Se llama forma reducida de un polinomio, a aquella en la que se ha simplificado, sumando los términos semejantes.
- Se llama grado de un polinomio, al mayor de los grados de los monomios que lo componen cuando el polinomio se ha puesto en forma reducida.
a) El polinomio 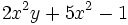 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
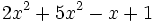 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 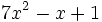 . Es de grado 2.
. Es de grado 2.Valor numérico de un polinomio
- Si en un polinomio se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico del polinomio para los valores de las letras dados.
- Un número se dice que es una raíz de un polinomio si el valor numérico del polinomio para dicho número es cero.
El número 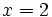 es una raíz del polinomio
es una raíz del polinomio 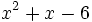 .
.
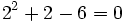
|
Actividad: Valor numérico y raíces de un polinomio Calcula el valor numérico del polinomio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
De a) y c) se deduce que x=2 y x=1 son raíces del polinomio. Prueba a introducir lo siguiente: roots x^2-3x+2 |
Operaciones con polinomios
Suma y resta de polinomios
Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.
Producto de un monomio por un polinomio
Para multiplicar un monomio por un polinomio, se multiplica el monomio por cada término del polinomio y se suman los resultados.
Producto de polinomios
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.
|
Actividad: Operaciones con polinomios
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Sacar factor común
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión
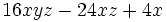
El factor común, que se repite en los tres sumandos, es
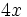 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 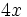 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
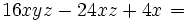
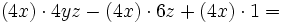
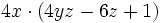
|
Actividad: Sacar factor común
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
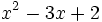 en los casos:
en los casos:
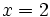 b)
b) 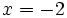 c)
c)