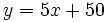Expresión analítica de una función (3ºESO Académicas)
De Wikipedia
| Revisión de 18:40 5 nov 2016 Coordinador (Discusión | contribuciones) (→Expresión analítica de una función) ← Ir a diferencia anterior |
Revisión de 18:48 5 nov 2016 Coordinador (Discusión | contribuciones) (→Expresión analítica de una función) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| {{p}} | {{p}} | ||
| {{Wolfram: Tabla de valores de una función}} | {{Wolfram: Tabla de valores de una función}} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad: ''Expresión analítica de una función''|cuerpo= | ||
| + | |||
| + | {{ai_cuerpo | ||
| + | |enunciado={{p}} | ||
| + | Unos alumnos de ESO disponen de una cuerda de 24 metros de longitud. Con ella deben construir rectángulos en el patio de su centro. | ||
| + | {{p}} | ||
| + | {{b4}}'''1.''' Haz una tabla de valores donde se relacione la base de los rectángulos y su área. | ||
| + | {{b4}}'''2.''' Halla una expresión que te permita calcular el área de cualquiera de esos rectángulos, conocida su base. | ||
| + | {{b4}}'''3.''' ¿Para que valor de la base se consigue un rectángulo de área máxima?. ¿Qué tiene de particular es valor? | ||
| + | |actividad=Comprueba el proceso en la siguiente escena: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Tablas_y_expresiones_algebraicas/teg_2_2.html | ||
| + | width=530 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Tablas_y_expresiones_algebraicas/teg_2_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | }} | ||
| + | |||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Wolfram: Máximos y mínimos}} | {{Wolfram: Máximos y mínimos}} | ||
Revisión de 18:48 5 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 152)
Expresión analítica de una función
La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.
Ejemplo: Expresión analítica de una función
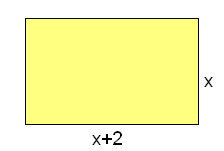
Un rectángulo mide 2 cm más de largo que de ancho.
- Halla la expresión analítica de la función que relaciona su área con su lado menor. Halla su dominio.
- Halla la expresión analítica de la función que relaciona su perímetro con su lado menor. Halla su dominio.
- Haz una tabla de valores para cada función.
- Representa gráficamente las dos funciones anteriores.
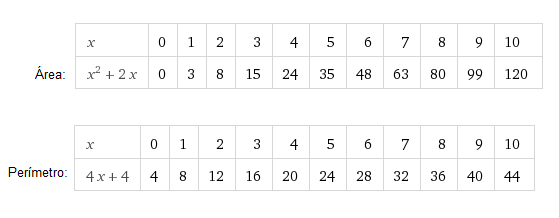
3. Tablas de valores:
4. Representación gráfica: A partir de los valores de las tablas anteriores, dibujamos los puntos de las gráficas: la dell área (en verde) y la del perímetro (en marrón).
Tutorial en el que se explican los conceptos básicos de la función y de su expresión analítica (expresión en forma de fórmula): variable independiente, dependiente, imagen, preimagen, dominio, recorrido...
Representación gráfica de funciones básicas
Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba. Obtén la expresión analítica que relaciona el volumen "V" de la caja en función del lado "x".
Expresa el área "A" de un triángulo equilátero en función de sus lado "L".
Dada la ecuación 4a + 7b = -52, encuentra la expresión analítica de la función a = f(b) que relacione la variable independiente b con la variable dependiente a, es decir, que exprese a en función de b.
Tutorial en el que se trabaja con las funciones definidas por partes en fórmulas, cálculo de imágenes y preimágenes de valores.
Actividades con las que aprenderás a obtener la expresión analítica de una función descrita mediante un enunciado.
Escribir funciones a partir de ecuaciones.
|
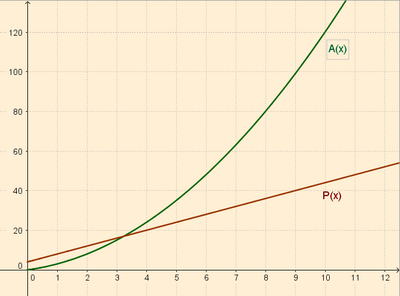
Actividad: Expresión analítica de una función Dadas las funciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Actividad: Expresión analítica de una función Unos alumnos de ESO disponen de una cuerda de 24 metros de longitud. Con ella deben construir rectángulos en el patio de su centro. 1. Haz una tabla de valores donde se relacione la base de los rectángulos y su área. 2. Halla una expresión que te permita calcular el área de cualquiera de esos rectángulos, conocida su base. 3. ¿Para que valor de la base se consigue un rectángulo de área máxima?. ¿Qué tiene de particular es valor? |
|
Actividad: Extremos relativos Nota para los cursos de secundaria: Algunas de las siguientes actividades son sólo ilustrativas ya que su resolución manual requiere conocimientos de 1º de bachillerato.
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Determinación del dominio de una función
El dominio de una función puede estar determinado o limitado por diferentes razones:
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
(Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, el lado no puede tomar valores negativos)
- Por voluntad de quien propone la función (A veces nos puede interesar estudiar sólo un trozo de la función).
Ejemplos: Dominio de una función dada por una expresión analítica
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
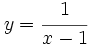
- b)
- c)
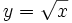
- c)
- d)
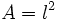 (Área de un cuadrado de lado
(Área de un cuadrado de lado 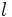 )
)
- d)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
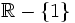 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
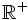 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
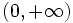 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Intervalos. Notación.
Dominio de una función.
Rango o imagen de una función.
Conceptos de dominio y rango de una función. Ejemplos
Dominio y rango de una función. Ejemplos.
Halla el dominio de 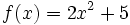 .
.
Halla el dominio de 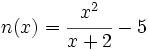 .
.
Halla el dominio de 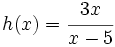 .
.
Halla el dominio de 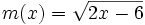 .
.
Halla el dominio de 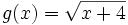 .
.
Halla el dominio de 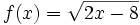 .
.
Dominio de una función dada por su expresión analítica.
|
Actividad: Dominio e imagen de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Variables discretas y continuas
En una función, la variable independiente puede ser:
- Continua: Si toma valores en intervalos. En consecuencia, siempre toma infinitos valores. La gráfica de la función estará formada por trazos.
- Discreta: Si los valores que toma la variable están separados (no toma valores en ningún intervalo). Puede tomar un número finito o infinito de valores. La gráfica de la función estará formada por puntos separados.
- Son variables continuas: El peso de una persona, la velocidad de un móvil, la altura de un triángulo, etc. De forma más general, una variable que tome valores en el conjunto de los números reales, en un intervalo real o en la unión de varios intervalos reales.
- Son variables discretas: El número de hijos de una familia, el número de trabajadores de una plantilla, el número de alumnos de un curso, etc. De forma más general, una variable que tome valores en el conjunto de los números enteros o en un subconjunto suyo.
En la papelería de la esquina compramos bolígrafos a 0.30 €, cada uno. Relaciona el número de bolígrafos comprados y el precio de la compra.
Tabla de valores:
a) Completa la tabla:
bolígrafos |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
precio |
Gráfica:
Para representar gráficamente una función utilizamos unos ejes cartesianos con una escala adecuada. En el eje horizontal representamos el número de bolígrafos que compramos. En el eje vertical representamos el precio de la compra. Para cada valor que le asignes al número de bolígrafos se marca en su vertical el precio de esos bolígrafos con un punto rojo.
En la parte inferior de la escena asígnale a la variable bolígrafos los valores de la tabla anterior y observa su precio, es decir, la altura donde se coloca el punto rojo.
b) ¿Cuáles son las escalas utilizadas en la gráfica?, es decir: ¿qué mide un cuadradito cualquiera del eje horizontal? y ¿qué mide un cuadradito cualquiera del eje vertical?
c) Fijándote en la gráfica, ¿cuánto cuestan 16 bolígrafos?. ¿Cuántos bolígrafos te dan por 3,60 €?
d) ¿Tiene sentido unir los puntos rojos de la gráfica? ¿Por qué?
e) ¿Cuál es el dominio y el recorrido de esta función?
Vamos al mercado a comprar patatas. El precio de 1 kg es de 0.30 €. Relaciona el número de kilos de patatas adquiridos y su coste.
El siguiente ejemplo es muy similar al anterior. Queremos comprar patatas a 0,30 € el kilo. Podemos construir una tabla y una gráfica idénticas a las anteriores salvo que en el eje horizontal representamos los kilos de patatas.
Pero hay una importante diferencia entre ambos ejemplos: no podemos comprar fracciones de bolígrafos (1.5 o 2.7 bolígrafos) y en cambio sí podemos comprar fracciones de kilos de patatas (1.5 o 2.7 kilos de patatas).
Tabla de valores:
a) Calcula y anota los precios de las siguientes cantidades de patatas. Asígnale esos valores a la variable kilos de la escena siguiente.
kilos de patatas |
0 | 1 | 1,5 | 2 | 2,7 | 5 | 5,7 | 7 |
precio |
Gráfica:
b) ¿Tiene sentido ahora unir los puntos rojos de la gráfica?
Compuébalo en la escena asignándole a la variable kilos el valor 0 y a continuación, mantén pulsado el botón del ratón sobre la fecha superior de los kilos de patatas.
En el primer caso, la gráfica estaba formada por puntos aislados. En este segundo caso, la gráfica es una línea continua.
c) ¿Cuál es el dominio y el recorrido de esta función?
|
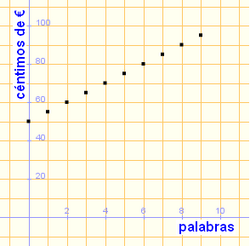
Ejercicio resuelto: Variables discretas y continuas Poner una anuncio por palabras cuesta una cantidad fija de 0.50 €, más 0.05 € por cada palabra.
|
Ejercicios propuestos
|
Ejercicios propuestos: Expresión analítica de una función |
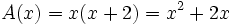
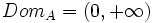
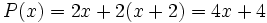
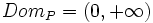
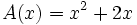
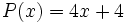
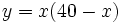
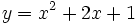
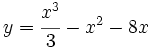 .
.
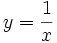 .
.