Ángulos en la circunferencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:15 24 nov 2016 Coordinador (Discusión | contribuciones) (→Propiedades) ← Ir a diferencia anterior |
Revisión de 14:32 24 nov 2016 Coordinador (Discusión | contribuciones) (→Propiedades) Ir a siguiente diferencia → |
||
| Línea 33: | Línea 33: | ||
| #Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | #Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | ||
| #La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | #La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | ||
| - | #Todo ángulo inscrito en una semicircunferncia es recto.{{p}} | + | #Todo ángulo inscrito en una semicircunferncia es recto. |
| - | |demo={{p}} | + | |
| - | #'''Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.''' | + | |
| - | #'''La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.''' | + | |
| - | Arrastra los puntos A y B. | + | |
| - | *Describe lo que observas: ¿qué relación hay entre las medidas de los tres ángulos destacados? | ||
| - | |||
| - | Cambia ahora la posición de P y Q | ||
| - | |||
| - | *¿Se sigue cumpliendo la relación? | ||
| - | |||
| - | Desliza el punto verde y describe lo que observes | ||
| - | |||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_1.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | ---- | ||
| - | #'''Todo ángulo inscrito en una semicircunferncia es recto:''' | ||
| - | |||
| - | Sea AB un diámetro de la circunferencia: {{sube|porcentaje=+20%|contenido=<math>\widehat{AOB}=180^o</math>}}. Por el apartado a), el ángulo inscrito <math>\widehat{AOB}=\cfrac{180^\circ}{2}=90^\circ</math>. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_2.html | ||
| - | width=780 | ||
| - | height=460 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/angulos_circunferencia_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Observa y manipula la figura: | ||
| - | |||
| - | *¿Cuál es la posición del triángulo APB respecto de la semicircunferencia? | ||
| - | *¿Cuánto estimas que puede medir el ángulo en P? | ||
| - | |||
| - | Desliza el punto verde y observa. | ||
| - | |||
| - | *¿Qué relación hay entre el ángulo verde (APB) y el azul (AOB)? | ||
| - | *¿Cuál será la medida de cada uno de ellos? | ||
| - | *Como conclusión: ¿qué se puede decir de los ángulos inscritos en una semicircunferencia? | ||
| - | |||
| - | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás comprobar la realción que hay entre ángulos centrales y ángulos inscritos en una circunferencia. | + | |descripcion=En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia. |
| |enlace=[https://ggbm.at/AqY3Dnyq Relación entre ángulos centrales e inscritos en una circunferencia] | |enlace=[https://ggbm.at/AqY3Dnyq Relación entre ángulos centrales e inscritos en una circunferencia] | ||
| + | }}{{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia. | ||
| + | |enlace=[https://ggbm.at/dSeCqqBp Ángulo inscrito en una semicircunferencia] | ||
| }} | }} | ||
| + | }}{{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 14:32 24 nov 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
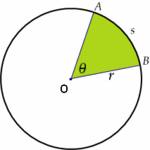
Ángulo central
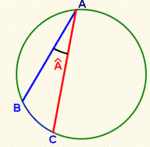
Ángulo inscrito
Propiedades
Propiedades
- Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
- La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- Todo ángulo inscrito en una semicircunferncia es recto.
En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia.
Demostración:
{{{demo}}}
 y su arco correspondiente AB.
y su arco correspondiente AB.
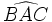 .
.