Ángulos en la circunferencia
De Wikipedia
| Revisión de 20:01 24 nov 2016 Coordinador (Discusión | contribuciones) (→Ángulo central) ← Ir a diferencia anterior |
Revisión de 20:02 24 nov 2016 Coordinador (Discusión | contribuciones) (→Ángulo inscrito) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| ==Ángulo inscrito== | ==Ángulo inscrito== | ||
| - | {{Caja_Amarilla | + | {{Ángulo inscrito}} |
| - | |texto= | + | |
| - | {{Tabla75|celda1=Se llama '''ángulo inscrito''' en una circunferencia al que tiene su vértice sobre la circunferencia y sus lados la cortan. | + | |
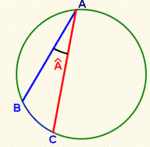
| - | En la figura está representado el ángulo inscrito <math>\widehat{BAC}</math>. | + | |
| - | |celda2=<center>[[Imagen:ang_inscrito.gif|150px]]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | ===Propiedades=== | + | |
| - | {{Teorema_sin_demo | + | |
| - | |titulo=Propiedades | + | |
| - | |enunciado= | + | |
| - | #Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. | + | |
| - | #La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. | + | |
| - | #Todo ángulo inscrito en una semicircunferencia es recto. | + | |
| - | }} | + | |
| - | Las dos primeras propiedades se pueden comprobar en la siguiente escena: | + | |
| - | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia. | ||
| - | |enlace=[https://ggbm.at/AqY3Dnyq Relación entre ángulos centrales e inscritos en una circunferencia] | ||
| - | }} | ||
| - | {{p}} | ||
| - | La tercera propiedad la puedes comprobar en esta otra escena: | ||
| - | |||
| - | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia. | ||
| - | |enlace=[https://ggbm.at/dSeCqqBp Ángulo inscrito en una semicircunferencia] | ||
| - | }} | ||
| ==Otros ángulos== | ==Otros ángulos== | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
Revisión de 20:02 24 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
Tabla de contenidos |
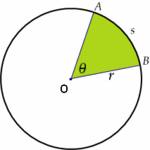
Ángulo central
En esta actividad podrás ver cómo es un ángulo central y el arco de circunferencia que determina.
Ángulo inscrito
Propiedades
Propiedades
- Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
- La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- Todo ángulo inscrito en una semicircunferencia es recto.
Las dos primeras propiedades se pueden comprobar (no es una demostración) en la siguiente escena:
En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
La tercera propiedad la puedes comprobar en esta otra escena:
En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia.
En esta actividad podrás ver cómo es un ángulo inscrito y su relación con el ángulo central correspondiente.
En esta actividad podrás ver cómo un ángulo inscrito en una semicircunferencia es recto.
Otros ángulos
En esta escena podrás ver los distintos tipos de ángulos que puede haber en una circunferencia: central, inscrito, semiinscrito, circunscrito, interior, exterior.
En esta escena podrás practicar el cálculo del valor de distintos tipos de ángulos en una circunferencia.
 y su arco correspondiente AB.
y su arco correspondiente AB.
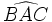 .
.