Problemas de proporcionalidad (3ºESO Académicas)
De Wikipedia
| Revisión de 19:48 25 nov 2016 Coordinador (Discusión | contribuciones) (→Proporcionalidad simple) ← Ir a diferencia anterior |
Revisión de 18:47 5 may 2017 Coordinador (Discusión | contribuciones) (→Proporcionalidad simple directa) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| {{b4}}<math>x=\frac{315\,000 \cdot 8}{120\,000}= 21</math> camiones | {{b4}}<math>x=\frac{315\,000 \cdot 8}{120\,000}= 21</math> camiones | ||
| }} | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 1 | ||
| + | |duracion=3'02" | ||
| + | |sinopsis=Se necesitan 70 galones de pintura para embellecer 5 casas de un condominio. ¿Que cantidad de pintura se requiere para 12 casas similares? | ||
| + | |url1=https://www.youtube.com/watch?v=hP6F-0oDvGk | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 2 | ||
| + | |duracion=2'31" | ||
| + | |sinopsis=Si una máquina copiadora tarda 8 segundos en sacar 20 copias, ¿cuánto tiempo tardará en sacar 45 copias? | ||
| + | |url1=https://www.youtube.com/watch?v=33CPzPuBSno | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 36: | Línea 50: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Proporcionalidad simple inversa=== | ===Proporcionalidad simple inversa=== | ||
| {{Ejemplo | {{Ejemplo | ||
Revisión de 18:47 5 may 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 44)
Proporcionalidad simple
Proporcionalidad simple directa
Ejercicio resuelto: Proporcionalidad simple directa
Para transportar 120000 l de agua, se necesitan 8 camiones cisterna. ¿Cuántos camiones se necesitarán para transportar 315000 l?
A más volumen de agua a transportar, más camiones se necesitarán. Las magnitudes "volumen de agua" y "nº de camiones" son directamente proporcionales:
Regla de tres simple directa:
Volumen (l) nº camiones
---------- D -----------
120000 ------> 8
315000 ------> x
| 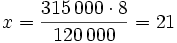 camiones camiones
|
Se necesitan 70 galones de pintura para embellecer 5 casas de un condominio. ¿Que cantidad de pintura se requiere para 12 casas similares?
Si una máquina copiadora tarda 8 segundos en sacar 20 copias, ¿cuánto tiempo tardará en sacar 45 copias?
Resuelve problemas de regla de tres simple directa.
Proporcionalidad simple inversa
Ejercicio resuelto: Proporcionalidad simple inversa
6 pintores tardan 8 días en pintar una casa. ¿Cuánto tardarán 4 pintores en realizar la misma tarea?
A menos pintores, más días tardarán en hacer la misma tarea. Las magnitudes "nº de pintores" y "tiempo" son inversamente proporcionales:
Regla de tres simple inversa:
nº pintores tiempo (días)
----------- I ------------
6 ------> 8
4 ------> x
| 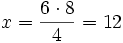 días días
|
Resuelve problemas de regla de tres simple inversa.
Resuelve problemas de regla de tres simple. Tendrás que averiguar si son directas o inversas.
(Pág. 45)
Proporcionalidad compuesta
Ejercicio resuelto: Proporcionalidad compuesta
Un solador embaldosa 260 m2 de suelo en 5 días trabajando 8 horas diarias. Se compromete a embaldosar un suelo de 500 m2 en 7 días. ¿Cuántas horas diarias tiene que trabajar?
| Tenemos tres variables: Superficie, número de días y numero de horas diarias.
Si fijamos la superficie, a máyor número de días, menor número de horas de trabajo diarias: La proporcionalidad es inversa. Si fijamos el número de días, a mayor superficie, mayor número de horas de trabajo diarias: La proporcionalidad es directa. Superficie Nº de días Nº horas diarias
---------- ---------- I ----------------
260 ------> 5 ------> 8
500 ------> 7 ------> x
└---------------------------------------┘
D
| 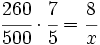
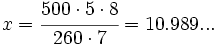
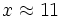 horas diarias horas diarias |
Ejercicios propuestos
|
Ejercicios propuestos: Proporcionalidad |

