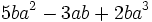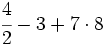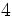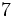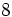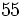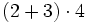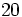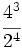Números naturales
De Wikipedia
| Revisión de 05:51 1 jun 2017 Coordinador (Discusión | contribuciones) (→Números naturales) ← Ir a diferencia anterior |
Revisión de 06:03 1 jun 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las potencias de naturales) Ir a siguiente diferencia → |
||
| Línea 98: | Línea 98: | ||
| }} | }} | ||
| - | ====Propiedades de las potencias de naturales==== | + | ===Propiedades de las potencias de naturales=== |
| - | {{Propiedades potencias naturales}} | + | {{propiedades potencias naturales}} |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Propiedades de las potencias''|cuerpo= | + | {{Ejemplo: propiedades potencias naturales}} |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Propiedades de las potencias de números naturales. | + | |
| - | |actividad= | + | |
| - | En las siguientes escenas, para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena. | + | |
| {{p}} | {{p}} | ||
| - | * '''Producto de potencias de la misma base:''' | + | {{Videos: propiedades potencias naturales}} |
| - | + | ||
| - | El producto de varias potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la suma de los exponentes. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/producto_1.html | + | |
| - | width=550 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Cociente de potencias de la misma base:''' | + | |
| - | + | ||
| - | El cociente de dos potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la resta de los exponentes. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/cociente_1.html | + | |
| - | width=550 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Potencia de exponente 0:''' | + | |
| - | + | ||
| - | Sigue actuando sobre la escena anterior, haz que los dos exponentes sean iguales, ello dará como resultado una potencia de exponente 0. Observa el valor de esa potencia. | + | |
| - | + | ||
| - | Habrás descubierto que: Una potencia de exponente 0 vale 1. | + | |
| - | + | ||
| - | * '''Potencia de una potencia:''' | + | |
| - | + | ||
| - | La potencia de una potencia equivale a una potencia simple cuya base es la misma y cuyo exponente es el producto de los exponentes. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/potpot_1.html | + | |
| - | width=550 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Potencia de un producto:''' | + | |
| - | + | ||
| - | La potencia de un producto equivale al producto de potencias cuyas bases son cada uno de los factores y cuyo exponente es el mismo. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/potprod_1.html | + | |
| - | width=550 | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2.''' Autoevaluación. | + | |
| - | |actividad= | + | |
| - | En las siguientes escenas rellena todas las cajas inferiores y pulsa "intro" al final. | + | |
| - | Cuando hayas marcado correctamente los tres aparecerá el mensaje CORRECTO, pero si marcas antes un número equivocado ya no aparecerá ese mensaje, por eso, no emplees los triángulos arriba y abajo para variar el número. | + | |
| - | + | ||
| - | * '''Elementos de una potencia:''' | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/prueba_1.html | + | |
| - | width=500 | + | |
| - | height=250 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Operaciones con potencias de la misma base:''' | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/prueba_2.html | + | |
| - | width=500 | + | |
| - | height=250 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Asocia los resultados de estas potencias:''' | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/prueba_3.html | + | |
| - | width=500 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3.''' Juegos. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/potencia/juegos.htm | + | |
| - | width=100% | + | |
| - | height=675 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión de 06:03 1 jun 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar Mi libreta | WIRIS Geogebra Calculadora Números naturales Aritmética |
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
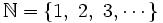
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Podemos representarlos en una recta:
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Operaciones con naturales
Suma y multiplicación de naturales
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Resta y división de naturales
La resta (o substracción)y la división (o cociente) de dos números naturales no siempre es otro número natural.
Propiedades de la suma y el producto de naturales
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
Sacar factor común
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión
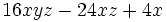
El factor común, que se repite en los tres sumandos, es
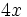 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 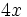 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
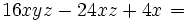
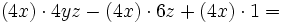
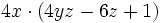
División de naturales
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
Potenciación de naturales
Una potencia de base  y exponente
y exponente  consiste en multiplicar
consiste en multiplicar  veces la base
veces la base  .
.
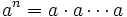
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo.
En la expresión de la potencia de un número consideramos dos partes:
- La base es el número que se multiplica por sí mismo
- El exponente es el número que indica las veces que la base aparece como factor.
Una potencia se escribe tradicionalmente poniendo el número base de tamaño normal y junto a él, arriba a su derecha se pone el exponente, de tamaño más pequeño.
Para nombrar o leer una potencia decimos primeramente el número base, después decimos lo referente al exponente. Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
|
Actividad Interactiva: Potencias
Actividad 1. Potencia de un número natural.
Actividad: Observa cómo varía el resultado al modificar la base y el exponente. Haz uso de la escena anterior y contesta en tu cuaderno:
|
Propiedades de las potencias de naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
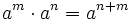
- 2. Cociente de potencias de la misma base:
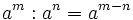
- 3. Potencia de un producto:
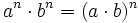
- 4. Potencia de un cociente:
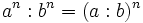
- 5. Potencia de otra potencia:
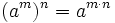
- Producto de potencias de la misma base:
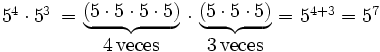
- Cociente de potencias de la misma base:
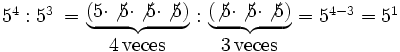
- Potencia de un producto:
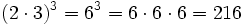
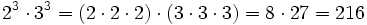
- Potencia de un cociente:
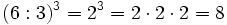
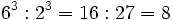
- Potencia de otra potencia:
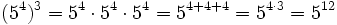
- Potencia cero: Cuando se vio la definición de potencia, dijimos que
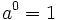 por convenio. Expliquemos ésto ahora un poco mejor:
por convenio. Expliquemos ésto ahora un poco mejor:
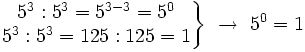
Potencias de números naturales con exponente natural.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
- Potencia de otra potencia.
- Ejemplos.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de otra potencia.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de un producto.
Aprende a calcular la potencia de un cociente.
Aprende a calcular la potencia de una potencia.
Enunciados de las propiedades de las potencias de números naturales.
Ejemplos de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Jerarquía de las operaciones con naturales
A la hora de operar con números naturales seguiremos las siguientes pautas:
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
|
Actividad Interactiva: Jerarquía de las operaciones
1. Operaciones combinadas.
Actividad: En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas. |
Ejercicios y problemas
Ejercicios
|
Ejercicios 1. Calcula:
Solución: a) 20 b) 48 c) 16 d) 30 2. Simplifica:
Solución: a) 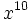 b) b) 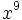 c) c) 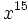 3. Simplifica:
Solución: a) 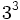 b) b) 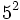 c) c) 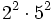 4. Extrae factor común:
Solución: a) 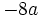 b) b) 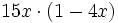 c) c) 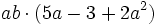 |
Problemas
|
Problemas
1. Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división)
2. Una empresa compra una máquina de café por 6.000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio mensual le ha aportado la máquina?
Solución: 214 € |
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |

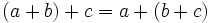
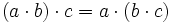
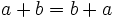
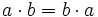
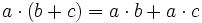
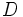 y
y 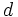 dos números naturales, con
dos números naturales, con 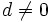 .
.
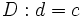
 , cociente.
, cociente.
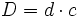 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 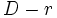 entre
entre 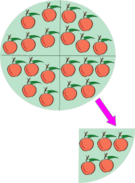
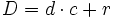

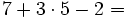
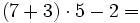
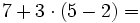
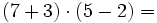
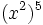 b)
b) 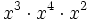 c)
c) 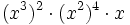
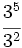 b)
b)  c)
c) 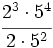
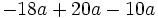 b)
b) 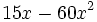 c)
c)