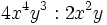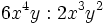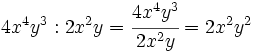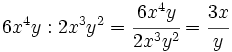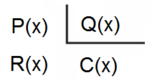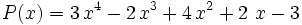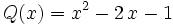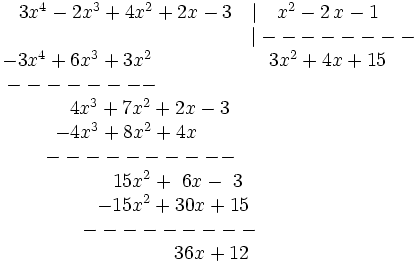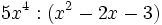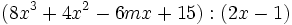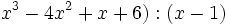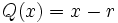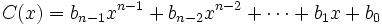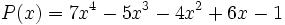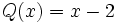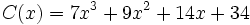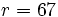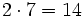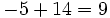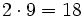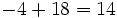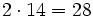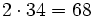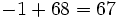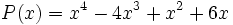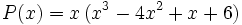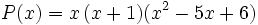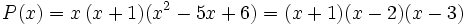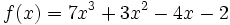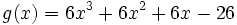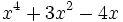Cociente de polinomios (3ºESO Académicas)
De Wikipedia
| Revisión de 07:27 3 jun 2017 Coordinador (Discusión | contribuciones) (→Factorización de polinomios) ← Ir a diferencia anterior |
Revisión de 07:27 3 jun 2017 Coordinador (Discusión | contribuciones) (→Factorización básica de polinomios) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| ==Factorización de polinomios== | ==Factorización de polinomios== | ||
| - | ==Factorización básica de polinomios== | + | ===Factorización básica de polinomios=== |
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| |titulo1=Factorización básica de polinomios | |titulo1=Factorización básica de polinomios | ||
Revisión de 07:27 3 jun 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 90)
División de monomios
Entenderemos la división entre monomios como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Aprende a dividir monomios
Divide:
- a)
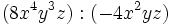
- b)
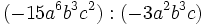
- c)
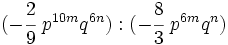
Divide los siguientes monomios:
- 54)
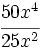 ; 55)
; 55) 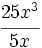 ; 56)
; 56) 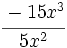 ; 57)
; 57) 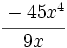
- 58)
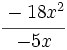 ; 59)
; 59) 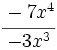 ; 60)
; 60) 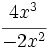 ; 61)
; 61) 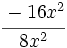
- 62)
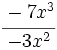 ; 63)
; 63) 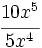 ; 64)
; 64) 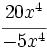 ; 65)
; 65) 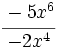
División de un polinomio entre un monomio
Para dividir un polinomio ente un monomio se divide cada uno de los monomios que componen el polinomio entre el monomio.
Aprende a dividir un polinomio entre un monomio
En este tutorial se explica la división de polinomios entre monomios.
Divide:
- a)
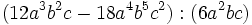
- b)
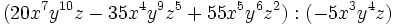
División de polinomios
La división polinómica es, en ciertos aspectos, similar a la división numérica.
Dados dos polinomios  (dividendo) y
(dividendo) y  (divisor) de modo que el grado de
(divisor) de modo que el grado de  sea mayor o igual que el grado de
sea mayor o igual que el grado de  y el grado de
y el grado de  sea mayor o igual a cero, siempre podremos hallar dos polinomios
sea mayor o igual a cero, siempre podremos hallar dos polinomios 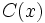 (cociente) y
(cociente) y 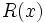 (resto) tales que:
(resto) tales que:
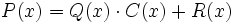
que también podemos representar como:
- El grado de
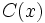 es igual a la diferencia entre los grados de
es igual a la diferencia entre los grados de  y
y  , mientras que el grado de
, mientras que el grado de 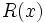 será, como máximo, un grado menor que
será, como máximo, un grado menor que  .
.
- Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.
División de polinomios. Ejemplos.
Siendo P(x) un polinomio de grado no inferior al polinomio Q(x), nos planteamos determinar los polinomios C(x) y R(x) tales que P(x) = Q(x).C(x) + R(x). De C(x) se dice "cociente" de la "división" entre P(x) y Q(x); de R(x) se dice "resto". Si R(x) = 0, la división se dice "exacta"; en tal caso, también se dice que P(x) es "divisible" por Q(x), o que P(x) es "múltiplo" de Q(x), o que Q(x) "divide" a P(x), o que Q(x) es "divisor" de P(x).
Cómo se hace la división de polinomios
División de polinomios
Calcula:
a) 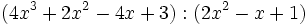
b) 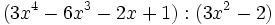
Calcula: 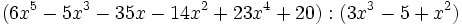
Calcula: 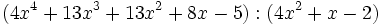
Calcula: 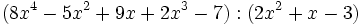
Calcula:
a) 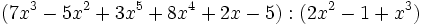
b) 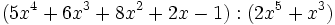
Calcula: 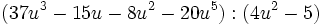
Divide los siguientes polinomios entre binomios:
- 1a)
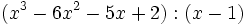
- 1b)
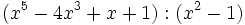
- 1c)
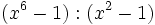
Divide los siguientes polinomios:
- 2a)
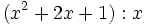
- 2b)
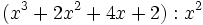
- 2c)
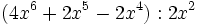
- 2d)
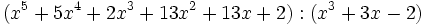
- 2e)
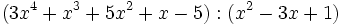
Divide los siguientes polinomios:
- 3a)
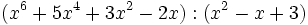
- 3b)
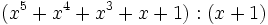
Divide los siguientes polinomios:
- 3c)
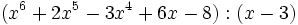
- 3d)
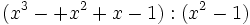
Divide los siguientes polinomios:
- 4a)
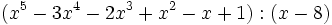
- 4b)
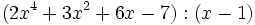
- 4c)
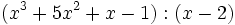
- 4d)
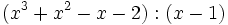
Divide los siguientes polinomios:
- 5a)
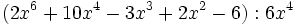
- 5b)
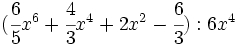
- 5c)
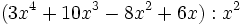
- 5d)
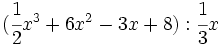
Divide los siguientes polinomios:
- 6a)
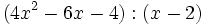
- 6b)
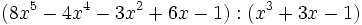
- 6c)
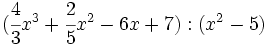
- 6d)
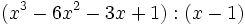
Indica qué divisiones de polinomios son exactas:
- 7a)
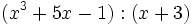
- 7b)
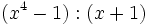
- 7c)
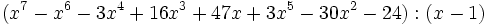
- 7d)
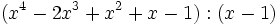
Divide los siguientes polinomios:
- 8a)
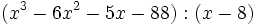
- 8b)
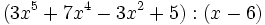
- 9a)
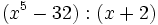
- 9b)
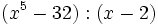
- 9c)
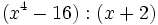
Divide los siguientes polinomios:
- 9d)
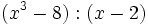
- 9e)
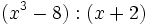
- 9f)
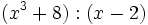
- 9g)
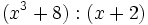
- 9h)
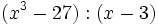
- 9i)
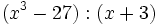
- 9j)
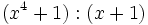
Divide los siguientes polinomios:
- a)
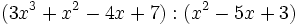
- b)
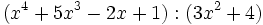
Método de Horner para la división de polinomios
Calcula: 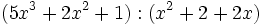
Halla el resto de la división:
Halla el resto de la división
sabiendo que la suma de los coeficientes del cociente es 28.
Ejercicios de autoevaluación sobre división de polinomios.
División de un polinomio por (x-a). Regla de Ruffini
Regla de Ruffini
La Regla de Ruffini es un procedimiento que nos permite dividir un polinomio entre un binomio de la forma 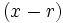 .
.
Debemos esta regla al matemático italiano Paolo Ruffini,
Procedimiento:
Vamos a dividir el polinomio
entre el binomio
para obtener el cociente
y el resto 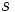 .
.
1. Trazamos dos líneas a manera de ejes. Cogemos los coeficientes de  y los escribimos ordenados. Entonces escribimos
y los escribimos ordenados. Entonces escribimos  en la parte inferior izquierda del eje, encima de la línea:
en la parte inferior izquierda del eje, encima de la línea:
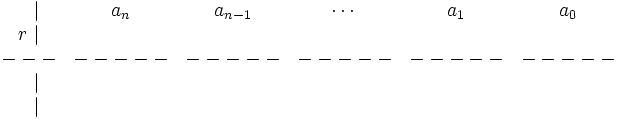
2. Pasamos el coeficiente más pegado a la izquierda,  , justo debajo de la línea, para obtener el primero de los coeficientes
, justo debajo de la línea, para obtener el primero de los coeficientes 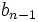 :
:
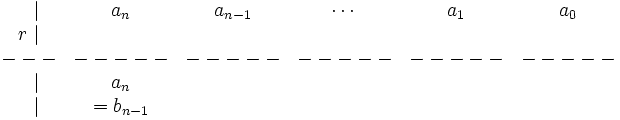
3. Multiplicamos el número más pegado a la derecha debajo de la línea por  y lo escribimos sobre la línea en la primera posición de la derecha:
y lo escribimos sobre la línea en la primera posición de la derecha:
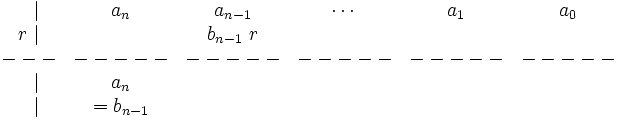
4. Añadimos los dos valores que hemos puesto en la misma columna:
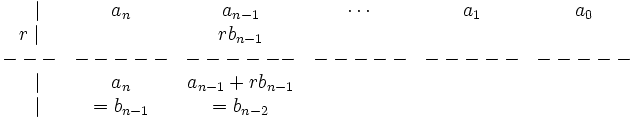
5. Repetimos los pasos 3 y 4 hasta que no tengamos más números:
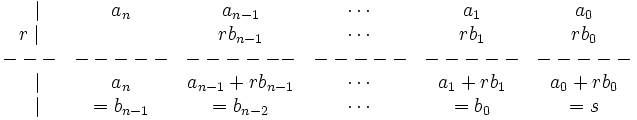
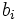 son los coeficientes del polinomio cociente
son los coeficientes del polinomio cociente 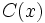 , cuyo grado será un grado menor que el del dividendo
, cuyo grado será un grado menor que el del dividendo  . El resto será
. El resto será 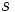 .
.Ejemplo: Regla de Ruffini
Divide los polinomios usando la regla de Ruffini:
| 7 -5 -4 6 -1
|
2| 14 18 28 68
--|-------------------
| 7 9 14 34 |67
|____
El resultado significa que:
|
|
Regla de Ruffini. Ejemplos.
Regla de Ruffini: Método rápido para realizar divisiones de polinomios entre binomios del tipo (x - a). Ejemplos.
La regla de Ruffini nos permite determinar supersónicamente el cociente y el resto de la división entre un polinomio P(x) y el polinomio Q(x) = x - a.
Cómo se aplica la Regla de Ruffini.
División de polinomios por el método de Ruffini para divisores del tipo (x-a).
Ejemplo de división de polinomios usando la regla de Ruffini.
2 ejemplos de división de polinomios usando la regla de Ruffini.
2 ejemplos de división mediante la regla de Ruffini
Otros 2 ejemplos de aplicación de la regla de Ruffini
Divide 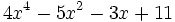 entre
entre 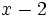 .
.
a) Divide 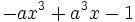 entre
entre 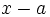
b) Divide 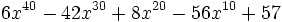 entre
entre 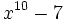
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 1a)
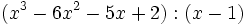
- 1b)
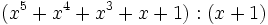
- 1c)
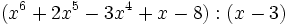
- 1d)
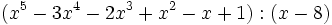
- 1e)
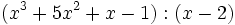
- 1f)
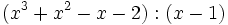
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 1g)
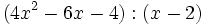
- 1h)
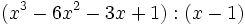
- 1i)
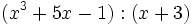
- 1j)
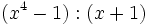
- 1k)
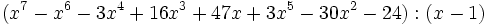
- 1l)
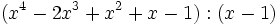
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 2a)
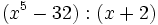
- 2b)
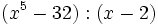
- 2c)
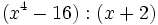
- 2d)
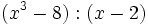
- 2e)
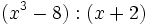
Divide los siguientes polinomios utilizando la regla de Ruffini:
- 2f)
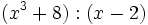
- 2g)
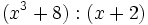
- 2h)
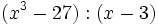
- 2i)
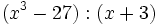
- 2j)
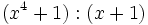
Divide los siguientes polinomios utilizando la regla de Ruffini:
- a)
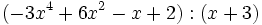
- b)
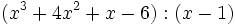
- c)
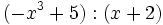
Ejercicios de autoevaluación sobre la regla de Ruffini.
Factorización de polinomios
Factorización básica de polinomios
En este tutorial se explica la factorización de polinomios más básica que es la de extraer factores, utilizar las igualdades notables y la propiedad de factorización de los polinomios de 2º grado.
Factorización de polinomios mediante la regla de Ruffini
Teorema
Las raíces enteras de un polinomio con coeficientes enteros son divisores de su término independiente.
Demostración:
En efecto, sea  una raíz entera de un polinomio con coeficientes enteros
una raíz entera de un polinomio con coeficientes enteros
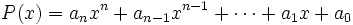
Entonces, como 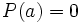 , tendremos que
, tendremos que
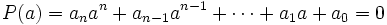
de donde, despejando el termino independiente
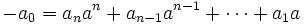
 en todos sus sumandos, es un múltiplo de
en todos sus sumandos, es un múltiplo de  , entonces
, entonces 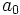 también. Luego
también. Luego  divide al término independiente.
divide al término independiente.Procedimiento para factorizar polinomios por Ruffini
Para factorizar un polinomio P(x) mediante la regla de Ruffini seguiremos los siguientes pasos:
- Por el teorema anterior, los candidatos a raíces del polinomio P(x) son los divisores (positivos y negativos) del término independiente.
- Para cada candidato a raíz, "a", efectuaremos la división de P(x) entre (x-a), mediante la regla de Ruffini.
- Si el resto es cero, "a" será una raíz de P(x). Si no, seguiremos probando con el siguiente candidato.
- Si "a" resulta ser una raíz, entonces tendremos una primera factorización: P(x)=(x-a)· Q(x), donde Q(x) tiene un grado menos que P(x).
- Seguiremos probando con los candidatos (incluido el último que resultó ser raíz) para factorizar Q(x) por Ruffini.
- El proceso para cuando no quedan candidatos o Q(x) tiene grado 1.
Ejemplo: Regla de Ruffini
Factoriza el siguiente polinomio:
Primero sacaremos factor común, con lo cual tendremos una primera factorización:
A continuación factorizamos 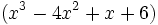 :
:
Los candidatos a raíces son los divisores (positivos y negativos) del término independiente. Como el término independiente es 6, los candidatos son: 1, -1, 2, -2, 3, -3, 6, -6.
Empezaremos probando con el 1:
| 1 -4 1 6
|
1| 1 -3 -2
--|---------------
| 1 -3 -2 |4
|____
Como el resto es distinto de cero, el 1 no es raíz. Pasamos a probar con -1:
| 1 -4 1 6
|
-1| -1 5 -6
--|---------------
| 1 -5 6 |0
|____
Como el resto es cero, -1 es raíz y 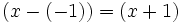 es un factor:
es un factor:
Seguimos aplicando Ruffini para factorizar el polinomio de grado 2. Probamos con -1, de nuevo ya que podría repetirse dicha raíz, pero resulta que no lo es. Probamos con el siguiente, 2:
| 1 -5 6
|
2| 2 -6
--|-------------
| 1 -3 |0
|____
Como el resto es cero, 2 es raíz y 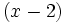 es un factor:
es un factor:
Método que nos permite factorizar polinomios de grado mayor que dos.
- Factorizar un polinomio P(x) es expresarlo como producto de otros de menor grado que él, y para ello hay que calcular los "ceros" de P(x), cosa no siempre fácil.
- Si "a" es un "cero" de P(x) y C(x) es el cociente de la división P(x)/(x-a), entonces P(x) = (x-a).C(x).
- Teorema de la factorización: si los coeficientes de un polinomio P(x) son números enteros, los ceros enteros de P(x) son divisores del término independiente de P(x).
- Si la suma de los coeficientes de P(x) es 0, pues apostar tranquilamente la vida a que el número 1 es un "cero" de P(x); o sea, P(x) es divisible por (x-1).
Cómo hacer una descomposición factorial de polinomios por Ruffini.
Factoriza los polinomios:
- a)
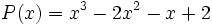
- b)
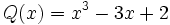
Factoriza el polinomio 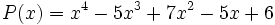
Factoriza el polinomio 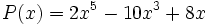
Factoriza el polinomio 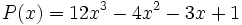 sabiendo que sólo tiene raíces fraccionarias.
sabiendo que sólo tiene raíces fraccionarias.
Hallar los puntos de intersección de las dos funciones polinómicas siguientes:
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8a)
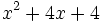
- 8b)
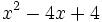
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8c)
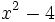
- 8d)
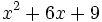
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8e)
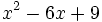
- 8f)
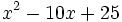
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8g)
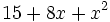
- 8h)
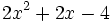
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8i)
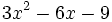
- 8j)
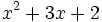
Factoriza los siguientes polinomios mediante la regla de Ruffini:
- 8k)
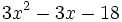
- 8l)
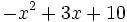
Ejercicios propuestos
|
Ejercicios propuestos: Cociente de polinomios |