Ecuaciones de segundo grado
De Wikipedia
| Revisión de 07:17 26 jun 2007 Coordinador (Discusión | contribuciones) (→Ecuación de segundo grado) ← Ir a diferencia anterior |
Revisión de 09:33 26 jun 2007 Coordinador (Discusión | contribuciones) (→Ecuación de segundo grado) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| {{Caja_Amarilla|texto=Una '''ecuación de segundo grado con una incógnita''' es aquella que se puede expresar de la forma: | {{Caja_Amarilla|texto=Una '''ecuación de segundo grado con una incógnita''' es aquella que se puede expresar de la forma: | ||
| <center><math>ax^2+bx+c=0, \quad a\ne 0</math></center> | <center><math>ax^2+bx+c=0, \quad a\ne 0</math></center> | ||
| + | que llamaremos '''forma general'''. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | '''Ejemplo:''' | + | {{Ejemplo|titulo=Ejemplo: ''Ecuación de segundo grado'' |
| + | |enunciado=Pasa a forma general la ecuación: | ||
| + | <center><math>3x-2x^2+5=-4x^2+3-x\;\!</math></center> | ||
| + | |sol= | ||
| + | Para ponerla en forma general, pasaremos todos los términos al miembro de la izquierda: | ||
| + | <center><math>3x-2x^2+5+4x^2-3+x=0\;\!</math></center> | ||
| + | Agrupando términos semejantes: | ||
| + | <center><math>2x^2+4x+2=0\;\!</math></center> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | ===Solución general del la ecuación de segundo grado=== | + | ==Soluciones de la ecuación de segundo grado== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Las soluciones de la ecuación de segundo grado son: | Las soluciones de la ecuación de segundo grado son: | ||
| Línea 20: | Línea 29: | ||
| donde el signo <math>(\pm)</math> significa que una solución se obtiene con el signo <math>(+)\;\!</math> y otra con el signo <math>(-)\;\!</math>. | donde el signo <math>(\pm)</math> significa que una solución se obtiene con el signo <math>(+)\;\!</math> y otra con el signo <math>(-)\;\!</math>. | ||
| }} | }} | ||
| - | ===Discriminante y número de soluciones de una ecuación de segundo grado=== | + | ==Discriminante y número de soluciones de una ecuación de segundo grado== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Llamamos '''discriminante''' de una ecuación de segundo grado a: | Llamamos '''discriminante''' de una ecuación de segundo grado a: | ||
| Línea 28: | Línea 37: | ||
| *Si <math>\triangle >0</math> la ecuación tiene dos soluciones. | *Si <math>\triangle >0</math> la ecuación tiene dos soluciones. | ||
| *Si <math>\triangle =0</math> la ecuación tiene una solución (doble). | *Si <math>\triangle =0</math> la ecuación tiene una solución (doble). | ||
| - | |||
| - | |||
| }} | }} | ||
| - | |||
| {{p}} | {{p}} | ||
| Línea 48: | Línea 54: | ||
| }} | }} | ||
| }} | }} | ||
| + | ==Ecuaciones de segundo grado incompletas== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Una ecuación de segundo grado <math>ax^2+bx+c=0\;\!</math> es incompleta, si ocurre uno de los siguientes casos: | ||
| + | *<math>b=0\;\!</math>: ax^2+c=0\;\!En este caso las soluciones son: <math>x=\pm \sqrt {-\cfrac{c}{a}}</math> | ||
| + | *<math>c=0\;\!</math>: En este caso las soluciones se obtienen sacando factor común e igualando a cero cada factor: <math>a^2x=\pm \sqrt {-\cfrac{c}{a}}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| ==Ecuaciones equivalentes== | ==Ecuaciones equivalentes== | ||
Revisión de 09:33 26 jun 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Ecuación de segundo grado
Una ecuación de segundo grado con una incógnita es aquella que se puede expresar de la forma:
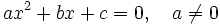
que llamaremos forma general.
Ejemplo: Ecuación de segundo grado
Pasa a forma general la ecuación:
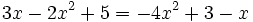
Para ponerla en forma general, pasaremos todos los términos al miembro de la izquierda:
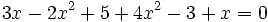
Agrupando términos semejantes:
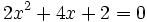
Soluciones de la ecuación de segundo grado
Las soluciones de la ecuación de segundo grado son:
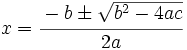
donde el signo 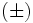 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 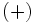 y otra con el signo
y otra con el signo 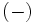 .
.
Discriminante y número de soluciones de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado a:
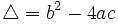
por tanto:
- Si
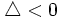 la ecuación no tiene solución.
la ecuación no tiene solución.
- Si
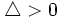 la ecuación tiene dos soluciones.
la ecuación tiene dos soluciones.
- Si
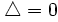 la ecuación tiene una solución (doble).
la ecuación tiene una solución (doble).
|
Actividad Interactiva: Solución de una ecuación de primer grado con una incógnita
Actividad 1: Ejemplos de soluciones de ecuaciones de primer grado con una incógnita.
Actividad: Pulsa los botones para ver más ecuaciones. |
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado 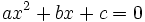 es incompleta, si ocurre uno de los siguientes casos:
es incompleta, si ocurre uno de los siguientes casos:
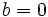 : ax^2+c=0\;\!En este caso las soluciones son:
: ax^2+c=0\;\!En este caso las soluciones son: 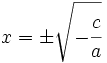
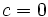 : En este caso las soluciones se obtienen sacando factor común e igualando a cero cada factor:
: En este caso las soluciones se obtienen sacando factor común e igualando a cero cada factor: 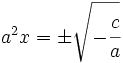
Ecuaciones equivalentes
Dos ecuaciones son equivalentes si tienen la misma solución.
Transformaciones que mantienen la equivalencia de las ecuaciones
- Sumar o restar la misma expresión en los dos miembros de la igualdad. Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.
- Multiplicar o dividir los dos miembros de la igualdad por un mismo número distinto de cero. Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.
Resolución de ecuaciones de primer grado
Para resolver una ecuación, hay que transformarla en otras ecuaciones equivalentes, cada vez más sencillas, hasta conseguir despejar la incógnita. Usaremos las transformaciones descritas en el apartado anterior.
|
Actividad Interactiva: Resolución de ecuaciones de primer grado
Actividad 1: Ecuaciones de primer grado sencillas (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones.
Actividad 2: Ecuaciones de primer grado con paréntesis (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones.
Actividad 3: Ecuaciones de primer grado con denominadores (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones. |
Resolución de problemas mediante ecuaciones de primer grado
Para resolver un problema mediante una ecuación, hay que seguir los siguientes pasos:
- Determinar la incógnita.
- Expresar el enunciado del problema en lenguaje algebraico, es decir, escribir una ecuación en la que intervenga la incógnita.
- Resolver la ecuación, es decir, halla el valor de la incógnita.
- Dar la solución del problema, a partir del valor obtenido de la incógnita.
|
Actividad Interactiva: Resolución de problemas mediante ecuaciones de primer grado
Actividad 1: Problemas resueltos.
Actividad: Pulsa el botón EJEMPLO para ver más problemas. Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes. |

