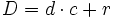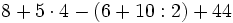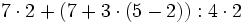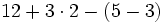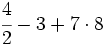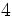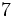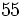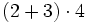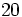Números naturales: Operaciones
De Wikipedia
| Revisión de 20:02 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Suma y multiplicación de naturales== | + | ==Introducción== |
| - | La '''suma''' (o adición) y la '''multiplicación''' (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición interna]'''. | + | {{AI_cidead |
| + | |titulo1=Para empezar | ||
| + | |descripcion=*Sabrías sumar de forma fácil y sin calculadora los 100 primeros números naturales? | ||
| + | *El misterioso número 6174. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena1/1quincena1_presenta_1a.htm | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | ==Resta y división de naturales== | + | ==Suma y resta de números naturales== |
| - | La '''resta''' (o substracción)y la '''división''' (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son '''[http://es.wikipedia.org/wiki/Operaci%C3%B3n_matem%C3%A1tica leyes de composición externa]'''. | + | {{Suma y resta de números naturales}} |
| {{p}} | {{p}} | ||
| - | ===Propiedades de la suma y el producto de naturales=== | + | ===Suma=== |
| - | La suma y la multiplicación cumplen las siguientes propiedades: | + | {{suma de naturales}} |
| - | {{Caja Amarilla|texto= | + | |
| - | *'''Propiedad asociativa:''' | + | |
| - | ::<math>(a+b)+c=a+(b+c)\,\!</math> | + | |
| - | ::<math>(a \cdot b)\cdot c=a \cdot(b \cdot c)</math> | + | |
| - | *'''Propiedad conmutativa:''' | + | |
| - | ::<math>a+b=b+a\,\!</math> | + | |
| - | ::<math>a \cdot b=b \cdot a</math> | + | |
| - | *'''Propiedad distributiva:''' | + | |
| - | ::<math>a \cdot (b+c)=a \cdot b+a \cdot c</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{ejercicio | + | ===Propiedades de la suma de números naturales=== |
| - | |titulo=Problema: ''Operaciones con naturales'' | + | {{Propiedades de la suma de números naturales}} |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''1. '''Una empresa compra una máquina de café por 6.000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio mensual le ha aportado la máquina? | + | |
| - | |sol= 214 € | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ==Sacar factor común== | + | ===Resta=== |
| - | La propiedad distributiva sirve para simplificar expresiones '''sacando factor común'''. Veamos un ejemplo | + | {{Resta de naturales}} |
| {{p}} | {{p}} | ||
| - | {{Ejemplo | + | ==Multiplicación o producto de números naturales== |
| - | |titulo=Ejemplo: ''Sacar factor común'' | + | {{Multiplicacion de naturales}} |
| - | |enunciado= | + | |
| - | :Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> | + | |
| - | |sol= | + | |
| - | El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | + | |
| - | <center><math>16xyz-24xz+4x\;\!=</math>{{p}} | + | |
| - | <math>(4x) \cdot 4yz - (4x) \cdot 6z + (4x) \cdot 1=\;\!</math>{{p}} | + | |
| - | <math>4x \cdot (4yz-6z+1)</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{ejercicio | + | ===Propiedades de la multiplicación de números naturales=== |
| - | |titulo=Ejercicios: ''Sacar factor común'' | + | {{Propiedades de la multiplicación de números naturales}} |
| - | |cuerpo= | + | {{p}} |
| + | ===Producto por 10, 100, 1000, ....=== | ||
| + | {{Producto por 10, 100, 1000}} | ||
| + | {{p}} | ||
| + | ==División de números naturales== | ||
| + | {{División de naturales}} | ||
| + | {{p}} | ||
| + | ===Cociente por defecto y por exceso=== | ||
| + | {{Cociente por defecto y por exceso}} | ||
| + | {{p}} | ||
| + | ===Propiedades de la división de números naturales=== | ||
| + | {{Propiedades de la división de números naturales}} | ||
| + | {{p}} | ||
| + | ==Operaciones combinadas== | ||
| + | {{Operaciones combinadas con naturales}} | ||
| + | {{p}} | ||
| + | ==Calculadora== | ||
| + | ===Suma, resta, multiplicación y división=== | ||
| + | {{Casio FX-100MS: Suma, resta, multiplicación y división}} | ||
| - | {{ejercicio_cuerpo | + | ===Paréntesis=== |
| - | |enunciado= | + | {{Casio FX-100MS: Paréntesis}} |
| - | '''1. '''Extrae factor común: | + | ==Problemas== |
| - | + | {{AI_enlace | |
| - | :a) <math>-18a+20a-10a\,\!</math>{{b}}b) <math>15x-60x^2\,\!</math>{{b}}c) <math>5ba^2-3ab+2ba^3\;\!</math> | + | |titulo1=Autoevaluación |
| - | <p></p> | + | |descripcion=Problemas de autoevaluación sobre números naturales. |
| - | |sol= | + | |url1=http://es.educaplay.com/es/recursoseducativos/1145104/numeros_naturales___6__.htm |
| - | a) <math>-8a\,\!</math>{{b}}b) <math>15x \cdot (1-4x)\,\!</math>{{b}}c) <math>ab \cdot (5a-3+2a^2)</math> | + | |
| }} | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | ==División con naturales== | ||
| - | {{Caja_Amarilla|texto=La '''división''' puede verse como un reparto de un número de elementos ('''dividendo''') en un número de partes iguales ('''divisor'''), que da como resultado el número de elementos que corresponden a cada parte ('''cociente''') y un posible número de elementos sobrantes ('''resto'''). Si el resto es cero la división se llama '''exacta''', si no, se llama '''entera'''. | ||
| - | }}{{p}} | ||
| - | ===Algoritmo de la división=== | ||
| - | {{Teorema | ||
| - | |titulo=Algoritmo de la división | ||
| - | |enunciado= | ||
| - | :En toda división, el dividendo es igual al divisor por el cociente más el resto. | ||
| - | {{caja|contenido=<math>D=d \cdot c + r</math>}} | ||
| - | :donde <math>D\;\!</math> es el dividendo, <math>d\;\!</math> el divisor, <math>c\;\!</math> el cociente y <math>r\;\!</math> el resto. | ||
| - | |demo= | ||
| - | Ver demostración en [http://es.wikipedia.org/wiki/Algoritmo_de_la_divisi%C3%B3n Wikipedia] | ||
| - | }} | ||
| - | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| - | |titulo=Problema: ''División con naturales'' | + | |titulo=Problema: ''Operaciones con naturales'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | '''1. '''Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor? | + | '''1. '''Una empresa compra una máquina de café por 6000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio le ha aportado la máquina? |
| - | |sol= | + | |sol= 6420 € |
| - | El divisor es 14 (Aplicando la regla de la división) | + | |
| }} | }} | ||
| }} | }} | ||
| + | |||
| + | {{p}} | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar Mi libreta | WIRIS Geogebra Calculadora Números naturales Aritmética |
Tabla de contenidos |
Introducción
- Sabrías sumar de forma fácil y sin calculadora los 100 primeros números naturales?
- El misterioso número 6174.
Suma y resta de números naturales
Videotutorial que resume lo que vamos a ver en este apartado sobre la suma y resta de números naturales y sus propiedades.
Practica con las operaciones de suma y resta de números naturales y con sus propiedades.
Suma
- Sumar es unir, juntar, añadir.
- La suma o adición de dos números naturales, a y b, da como resultado otro número natural, c. Se representa: a+b=c.
- a y b reciben el nombre de sumandos.
- El resultado, c, se denomina suma.
El concepto de adición o suma en el conjunto de los números naturales.
El concepto de adición o suma en el conjunto de los números naturales.
Calcula:
a) 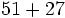
b) 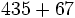
c) 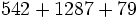
d) 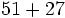
Calcula: 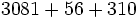
Calcula: 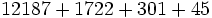
Calcula: 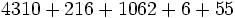
Cálculo mental con sumas.
Propiedades de la suma de números naturales
Propiedades de la suma
- Operación interna: el resultado de sumar dos números naturales es otro número natural.
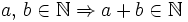
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
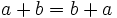
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
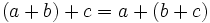
- Elemento neutro: El elemento neutro para la suma es el 0.
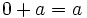
Propiedades de la suma de números naturales. Ejemplos.
Propiedades de la suma de números naturales. Ejemplos.
Propiedades conmutativa y asociativa de la suma de números naturales. Ejemplos.
El elemento neutro de la suma y del producto de números naturales. Ejemplos.
A look behind the fundamental properties of the most basic arithmetic operation, addition.
(Disponibles los subtítulos en inglés)
Aplicación de las propiedades asociativa y conmutativa de la suma. Ejemplos.
Usa la propiedad conmutativa de la suma para escribir la expresión 5 + 8 + 5 de una manera diferente. Comprueba que ambas expresiones dan el mismo resultado.
Usa la propiedad asociativa de la suma para escribir la expresión (77 + 2) + 2 de una manera diferente. Comprueba que ambas expresiones dan el mismo resultado.
Propiedades de la suma de números naturales.
Propiedades de la suma de números naturales.
Resta
- Restar es quitar, hallar lo que falta o lo que sobra, es decir, calcular la diferencia.
- La resta o sustracción de dos números naturales, a y b, se representa: a-b=c
- a es el minuendo, b el sustraendo y c la diferencia.
La resta de números naturales no cumple las propiedades de la suma:
- No es operación interna:
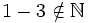 .
.
- No cumple la propiedad conmutativa:
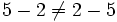
- No cumple la propiedad asociativa:
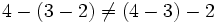
El concepto de sustracción en el conjunto de los números naturales.
Repaso de primaria sobre resta de números naturales.
Calcula:
a) 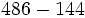
b) 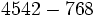
Calcula: 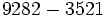
Calcula: 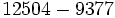
Calcula: 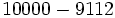
Cálculo mental con restas.
Ejercicios de autoevaluación sobre la resta de números naturales.
Multiplicación o producto de números naturales
Multiplicar es una forma abreviada de realizar una suma de sumandos iguales.
Videotutorial que resume lo que vamos a ver en este apartado sobre la multiplicación de números naturales y sus propiedades.
- Multiplicar dos números naturales consiste en sumar uno de los factores consigo mismo tantas veces como indica el otro factor.
- La multiplicación o producto de dos números naturales,
 y
y  , se representa
, se representa 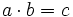 .
.
 y
y  se llaman factores y c se denomina producto.
se llaman factores y c se denomina producto.
El concepto de multiplicación en el conjunto de los números naturales.
Calcula:
a) 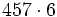
b) 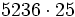
Calcula: 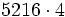
Calcula: 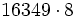
Calcula: 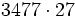
Calcula: 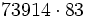
Calcula: 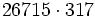
Calcula: 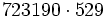
Cálculo mental con multiplicaciones.
Para construir con palillos una fila de cuatro cuadrados contiguos se necesitan 13 palillos. ¿Cuántos palillos se necesitarán para construir una fila de 26 cuadrados contiguos?
Si 8 máquinas producen 1500 piezas, ¿cuántas piezas fabricarán 40 máquinas del mismo tipo?
Propiedades de la multiplicación de números naturales
Propiedades de la multiplicación
- Operación interna: El producto de dos números naturales es otro número natural:
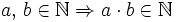
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
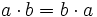
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
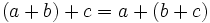
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
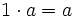
Propiedades conmutativa y asociativa del producto de números naturales. Ejemplos.
Propiedad distributiva de los números naturales. Ejemplos.
El elemento neutro de la suma y del producto de números naturales. Ejemplos.
Ejemplos de uso de la propiedad distributiva y de cómo se saca factor común.
Propiedad asociativa y conmutativa de forma visual.
Propiedad distributiva de forma visual.
Más formas de pensar en la multiplicación. Multiplicando usando la propiedad asociativa.
Otra forma de multiplicar usando la propiedad distributiva.
El elemento neutro de la multiplicación de números naturales es el 1.
The commutative property is common to the operations of both addition and multiplication and is an important property of many mathematical systems.
(Disponibles los subtítulos en inglés)
A look at the logic behind the associative and distributive properties of multiplication.
(Disponibles los subtítulos en inglés)
Usa la propiedad conmutativa de la multiplicación para multiplicar 2 · 34 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad asociativa de la multiplicación para multiplicar (12 · 3) · 10 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad distributiva de la multiplicación sobre la suma para calcular 4·(8 + 3).
Usa la propiedad distributiva de la multiplicación sobre la resta para calcular 5·(9 - 4).
Usa la propiedad distributiva de la multiplicación sobre la suma para sacar factor común en las siguientes expresiones:
- a) 20 + 30
- b) 90 + 27
- c) 55 + 35
- d) 12 + 75
Multiplica 6 · 7981 usando la propiedad distributiva.
Multiplica 78 · 65 usando la propiedad distributiva.
Propiedad conmutativa:
Introducción a la propiedad conmutativa del producto de números naturales.
Resumen de la propiedad conmutativa del producto de números naturales.
Propiedad conmutativa del producto de números naturales.
Propiedad asociativa:
Introducción a la propiedad asociativa del producto de números naturales.
Resumen de la propiedad asociativa del producto de números naturales.
Propiedad asociativa del producto de números naturales.
Propiedad distributiva:
Introducción a la propiedad distributiva del producto sobre la suma de números naturales.
Resumen de la propiedad distributiva del producto sobre la suma de números naturales.
Propiedad distributiva del producto sobre la suma de números naturales.
Saca factor común usando la propiedad distributiva del producto sobre la suma de números naturales.
Propiedades de la multiplicación:
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Ejemplo: Propiedad distributiva del producto
Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
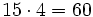
- Teresa------>
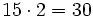
- Total--------->
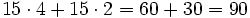 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
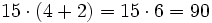 €
€
Producto por 10, 100, 1000, ....
Para multiplicar un número por la unidad seguida de ceros (10, 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).
Multiplicar números de 1 dígito por 10, 100 y 1000.
Multiplicando números de 1 dígito por múltiplos de 10.
Multiplicar números de 1 dígito por múltiplos de 10, 100 y 1000.
Multiplicando dos múltiplos de 10.
Multiplica números de 1 dígito por 10, 100 y 1000.
Multiplica por decenas.
Multiplica dos múltiplos de 10.
Multiplica números de 1 dígito por un múltiplo de 10, 100 y 1000
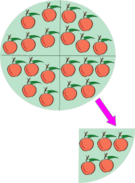
División de números naturales
El siguiente video resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Videotutorial que resume lo que vamos a ver en este apartado sobre la división de números naturales y sus propiedades.
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
El concepto de división exacta en el conjunto de los números naturales.
División exacta y entera de números naturales. Algoritmo de la división. Ejemplos.
Repaso sobre divisiones de números naturales por 1 o 2 cifras.
Aprende a dividir por una cifra
Aprende a dividir por dos cifras
Ejercicios de divisiones por 1, 2 o 3 cifras.
En esta actividad podrás comprobar si una división dada es exacta o no.
Cálculo con divisiones.
En una división con resto 24, ¿cuál es el valor mínimo del divisor?
Ejercicios de autoevaluación sobre la división de números naturales y sus propiedades.
|
Actividad: Cociente y resto Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Ejercicio: División con naturales
Al dividir 453 entre 32 se obtiene 5 de resto. ¿Cúal es el divisor?
Solución: El divisor es 14 (Aplicando la regla de la división) |
Cociente por defecto y por exceso
Ejemplo: Cociente por defecto y por exceso
Un autobús con 43 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.
- a) ¿Cuántos taxis completarán?
- b) ¿Cuántos taxis se necesitan?
- c) ¿cuál es el cociente por defecto y por exceso?
a) Completan 10 taxis y sobran 3 turistas. (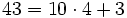 )
)
b) Se necesitan 11 taxis, aunque en el último taxi quede un asiento libre.
Propiedades de la división de números naturales
Propiedades
- No es una operación interna: La división de de números naturales no siempre es un número natural
- La división no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
- Si dividimos 0 por cualquier número distinto de 0, el resultado es 0.
- Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número.
Veamos ejemplos que ilustren estas propiedades:
- La división de números naturales no es una operación interna:
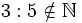
- La división de números naturales no cumple la propiedad conmutativa:
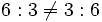
- La división de números naturales no cumple la propiedad asociativa:
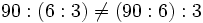
- La división de números naturales no cumple la propiedad distributiva:
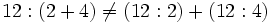
- Si dividimos 0 por cualquier número distinto de 0, el resultado es 0.:
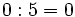
Para la última propiedad veremos un ejemplo:
Hagamos la división 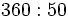
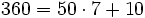 (Cociente=7; Resto=10)
(Cociente=7; Resto=10)Ahora dividimos el dividendo y el divisor por 10:
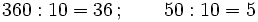
y volvemos a hacer la división:
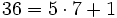 (Cociente=7; Resto=1)
(Cociente=7; Resto=1)Operaciones combinadas
Jerarquía de las operaciones
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las multiplicaciones y las divisiones.
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
- No se incluyen las potencias ni las raíces en este esquema, pues estas operaciones se veran en otro tema. Lo que haremos será resolverlas después de resolver los paréntesis, antes de las multiplicaciones y divisiones.
Efectúa las siguientes operaciones combinadas: 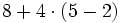
Solución:
- Los paréntesis
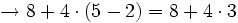
- Las multiplicaciones y divisiones
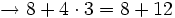
- Las sumas y restas
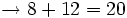
Prioridad en las operaciones combinadas de números naturales. Ejemplos.
Prioridad en las operaciones combinadas de números naturales. Ejemplos.
Prioridad en las operaciones combinadas de números naturales. Ejemplos.
Prioridad en las operaciones combinadas de números naturales:
a) 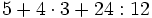
b) 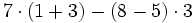
c) 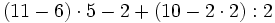
Calcula:
Calcula:
Escribe una expresión numérica que modele la siguiente situación, sin efectuar las operaciones:
"Arturo encontró 4 canicas y las agregó a las 5 canicas que ya traía en el bolsillo. Más tarde participó en una competición con sus amigos en donde triplicó sus canicas."
Calcula las siguientes expresiones y explica por qué los resultados obtenidos son diferentes:
- a)
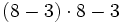
- b)
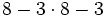
Correspondiente a 1º de ESO, en este vídeo se calculan una serie de operaciones combinadas con números naturales.
Correspondiente a 1º de ESO, en este vídeo se calculan una serie de operaciones combinadas con números naturales.
Correspondiente a 1º de ESO, en este vídeo se calculan una serie de operaciones combinadas con números naturales.
Practica las operaciones combinadas con números naturales y con su jerarquía.
Ejercicios sobre operaciones combinadas.
Actividades de sumas y restas con 3 números.
Operaciones combinadas sencillas.
Operaciones combinadas con paréntesis.
Traduce expresiones con paréntesis.
Crea expresiones con paréntesis a partir de enunciados.
Operaciones combinadas más complejas.
Operaciones combinadas a partir de enunciados.
Aviso: Debes introducir la expresión sin efectuar los cálculos. Usa "x" para indicar las multiplicaciones.
En esta escena podrás practicar la suma y resta con 4 números naturales, con o sin paréntesis.
En esta escena podrás practicar operaciones combinadas de sumas, restas, multiplicaciones, divisiones y paréntesis, con 3 números naturales.
En esta escena podrás practicar operaciones combinadas de sumas, restas, multiplicaciones, divisiones y paréntesis, con 4 números naturales.
Operaciones combinadas con 3 números.
Operaciones combinadas con 4 números:
En esta actividad debes escribir en la ventana bajo la escena el número que sigue al resolver la expresión y pulsar "intro". Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá.
Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final.
Al picar sobre inicio aparecerá otra expresión diferente de operaciones combinadas. Resuelve varias de ellas.
Operaciones combinadas más complejas (más de 4 números).
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Paréntesis
|
Calculadora: Paréntesis |
Problemas
Problemas de autoevaluación sobre números naturales.
|
Problema: Operaciones con naturales
1. Una empresa compra una máquina de café por 6000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio le ha aportado la máquina?
Solución: 6420 € |
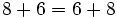
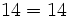
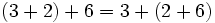
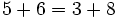
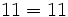
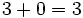
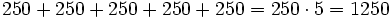 €
€
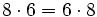
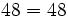
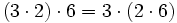

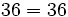
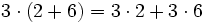
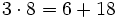
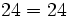
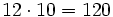
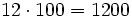
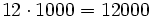
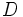 y
y 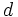 dos números naturales, con
dos números naturales, con 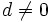 .
.
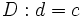
 , cociente.
, cociente.
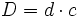 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 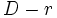 entre
entre