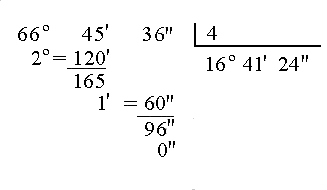Plantilla:División de ángulos
De Wikipedia
| Revisión de 09:05 7 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Para dividir un ángulo por un número natural dividimos los grados entre ese número. Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos. Dividimos los minutos. Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. Dividimos los segundos. | + | {{Caja_Amarilla|texto=La división de un ángulo por un número natural es una operación que consiste en separar el ángulo en tantas partes iguales como nos indique el número. |
| - | Analicemos el siguiente ejemplo: | + | *La división se realiza de forma '''analítica''' dividiendo la amplitud del ángulo entre el número natural correspondiente. |
| + | *La división '''gráfica''' resulta más compleja ya que no siempre se puede hacer con regla y compás.}} | ||
| + | {{p}} | ||
| + | Por ejemplo, la división de un ángulo en tres partes iguales (el famoso [https://es.wikipedia.org/wiki/Trisecci%C3%B3n_del_%C3%A1ngulo problema de la trisección del ángulo]), es imposible para la mayor parte de los ángulos. En cambio, siempre es posible calcular la división de un ángulo en dos partes iguales gráficamente, mediante el trazado de la [[Bisectriz de un ángulo (1º ESO)|bisectriz]] del ángulo. | ||
| + | |||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Construcción gráfica de la trisección de un ángulo recto, con regla y compás. | ||
| + | |enlace=[https://ggbm.at/jUQHdzJa Trisección de un ángulo recto] | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=División de un ángulo por un número|descripcion=Actividad en la que podrás ver como se dividen ángulos por números naturales. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_5d.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| + | Para dividir analíticamente un ángulo en sexagesimal, en forma compleja, entre un número natural: | ||
| + | |||
| + | #Dividimos los grados entre ese número. | ||
| + | #Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos. | ||
| + | #Dividimos los minutos. | ||
| + | #Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. #Dividimos los segundos. | ||
| + | }} | ||
| + | {{p}} | ||
| + | Veamos un ejemplo: | ||
| {{Ejemplo | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''División por un número en el sistema sexagesimal'' | + | |titulo=Ejemplo: ''División por un número en forma compleja'' |
| |enunciado= | |enunciado= | ||
| - | :Divide 66º 45' 36" entre 4. | + | Calcula la siguiente división de un ángulo en sexagesimal en forma compleja entre un número natural: |
| + | |||
| + | <center><math>(66^\circ \, 45' \, 36''):4</math></center> | ||
| + | |||
| |sol= | |sol= | ||
| <center>[[Imagen:division_angulos.gif]]</center> | <center>[[Imagen:division_angulos.gif]]</center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_enlace|titulo1=Actividad Interactiva: ''División de ángulos por un número'' | + | {{AI_descartes|titulo1=Actividad: ''División de ángulos por un número'' |
| - | |descripcion=Realiza en tu cuaderno las siguientes divisiones de ángulos: | + | |descripcion=Realiza en tu cuaderno las siguientes divisiones de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba: |
| :a) 56º 20' 40" : 5 | :a) 56º 20' 40" : 5 | ||
| Línea 20: | Línea 47: | ||
| :c) 125º 15' 30" : 3 | :c) 125º 15' 30" : 3 | ||
| |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo8.htm | |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo8.htm | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=División un ángulo entre un número en forma compleja|enunciado= | ||
| + | {{Video_enlace_sensei | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=7'13" | ||
| + | |sinopsis=División de un ángulo entre un número en forma compleja en sexagesimal. | ||
| + | |url1=https://www.youtube.com/watch?v=t5bpYGWv-qo | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=4'21" | ||
| + | |url1=https://www.youtube.com/watch?v=8CT4t3pytBA | ||
| + | |sinopsis=Calcula: (139º 34' 48") : 6 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=5'11" | ||
| + | |url1=https://www.youtube.com/watch?v=Ks9uz85FXUk | ||
| + | |sinopsis=Calcula: (50º 20' 26") : 12 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=5'13" | ||
| + | |url1=https://www.youtube.com/watch?v=TT7X5bl2h7o | ||
| + | |sinopsis=Calcula: (125º 37') : 9 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=4'03" | ||
| + | |url1=https://www.youtube.com/watch?v=ESYzDTneYl4 | ||
| + | |sinopsis=Calcula: (65º 21') : 3 | ||
| + | }} | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_tutomate | ||
| + | |titulo1=Multiplicación y división de ángulos | ||
| + | |duracion=9'37" | ||
| + | |sinopsis=Multiplicación y división en forma compleja, en el sistema sexagesimal. | ||
| + | |url1=https://www.youtube.com/watch?v=RME1Y5FmpVo&list=PLWRbPOo5oaTf2whhnJl7pa024DgsoHD74&index=3 | ||
| }} | }} | ||
Revisión actual
La división de un ángulo por un número natural es una operación que consiste en separar el ángulo en tantas partes iguales como nos indique el número.
- La división se realiza de forma analítica dividiendo la amplitud del ángulo entre el número natural correspondiente.
- La división gráfica resulta más compleja ya que no siempre se puede hacer con regla y compás.
Por ejemplo, la división de un ángulo en tres partes iguales (el famoso problema de la trisección del ángulo), es imposible para la mayor parte de los ángulos. En cambio, siempre es posible calcular la división de un ángulo en dos partes iguales gráficamente, mediante el trazado de la bisectriz del ángulo.
Construcción gráfica de la trisección de un ángulo recto, con regla y compás.
Actividad en la que podrás ver como se dividen ángulos por números naturales. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Procedimiento
Para dividir analíticamente un ángulo en sexagesimal, en forma compleja, entre un número natural:
- Dividimos los grados entre ese número.
- Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos.
- Dividimos los minutos.
- Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. #Dividimos los segundos.
Veamos un ejemplo:
Ejemplo: División por un número en forma compleja
Calcula la siguiente división de un ángulo en sexagesimal en forma compleja entre un número natural:
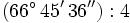
Realiza en tu cuaderno las siguientes divisiones de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" : 5
- b) 37º 42' 15" : 4
- c) 125º 15' 30" : 3
División de un ángulo entre un número en forma compleja en sexagesimal.
Calcula: (139º 34' 48") : 6
Calcula: (50º 20' 26") : 12
Calcula: (125º 37') : 9
Calcula: (65º 21') : 3
Multiplicación y división en forma compleja, en el sistema sexagesimal.