Plantilla:Def numeros reales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:34 23 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Tabla75|celda2=[[Image:cto_reales.png|right|300px]] | + | {{Tabla75|celda2=[[Image:cto_reales.jpg|right|300px|thumb|{{p}}El conjunto de los números reales{{p}}''<sub>de [http://www.portaleducativo.net portaleduativo.net]</sub>]]'' |
| |celda1= | |celda1= | ||
| {{Caja_Amarilla|texto=El conjunto de los '''números reales''' es el formado por la unión de los [[números racionales]] y de los [[números irracionales]] y se designa por <math>\mathbb{R}</math>. | {{Caja_Amarilla|texto=El conjunto de los '''números reales''' es el formado por la unión de los [[números racionales]] y de los [[números irracionales]] y se designa por <math>\mathbb{R}</math>. | ||
Revisión actual
El conjunto de los números reales es el formado por la unión de los números racionales y de los números irracionales y se designa por 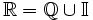 En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: 
| 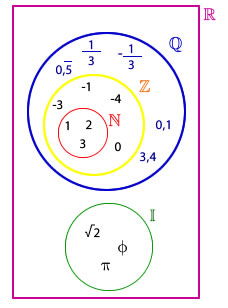 El conjunto de los números realesde portaleduativo.net |
 .
.

