Ángulos
De Wikipedia
| Revisión de 17:05 6 jul 2017 Coordinador (Discusión | contribuciones) (→Puntos cardinales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| Línea 129: | Línea 129: | ||
| ===Rumbo=== | ===Rumbo=== | ||
| - | {{Tabla75|celda2=[[Imagen:rumbo.jpg|250px|right|Posicionándonos en el origen de coordenadas, si nos moviésemos siguiendo la línea discontinua, nuestro rumbo sería N35ºE]]|celda1= | + | {{Tabla75|celda2=<center>[[Imagen:rumbo_cuad.jpg|200px]]Ejemplos de rumbos cuadrantales</center>|celda1= |
| - | {{Caja_Amarilla|texto= | + | |
| El '''rumbo''' es la dirección en la que nos movemos o navegamos, o en la cual nos dirigimos o miramos. Hay dos tipos: | El '''rumbo''' es la dirección en la que nos movemos o navegamos, o en la cual nos dirigimos o miramos. Hay dos tipos: | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | *'''Rumbo cuadrantal''' ('''rumbo'''): si lo expresamos como el ángulo agudo que forma el eje Norte-Sur con la dirección del avance. | ||
| - | *'''Rumbo cuadrantal''': si lo expresamos como el ángulo agudo que forma la línea Norte–Sur con la dirección de avance. | + | *'''Rumbo circular''' ('''azimut'''): si lo expresamos como el ángulo entre el eje Norte y la dirección del avance, medido de 0º a 360º. |
| - | + | ||
| - | *'''Rumbo circular''': si lo expresamos como el ángulo entre la dirección Norte y la dirección de avance, medido de 0º a 360º. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 142: | Línea 142: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos|contenido= | {{Ejemplo_simple|titulo=Ejemplos|contenido= | ||
| - | '''Ejemplo 1:''' En el siguiente gráfico, podemos decir que el rumbo de P a Q es N35°O, o bien, que Q está "35° al oeste del norte" de P. | + | '''Ejemplo 1:''' Para ir de P a Q podemos decir que el rumbo es N35°O, o bien que Q está "35° al oeste del norte" de P. (Ver Fig. 1) |
| - | <center>[[Imagen:rumbo2.jpg]]</center> | + | |
| {{p}} | {{p}} | ||
| + | '''Ejemplo 2:''' Un rumbo cuadrantal N65ºO significa 65º hacia el Oeste contados desde el Norte, lo que equivale a un rumbo circular de 295º. (Ver Fig. 2) | ||
| + | {{p}} | ||
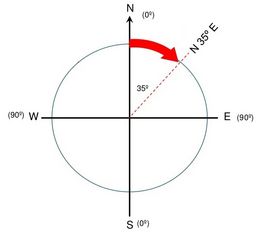
| + | '''Ejemplo 3:''' Un rumbo cuadrantal N35ºE significa 35º hacia el Este contados desde el Norte. En este caso coincide con el rumbo circular. (Ver Fig. 3) | ||
| + | |||
| ---- | ---- | ||
| - | '''Ejemplo 2:''' Un rumbo cuadrantal S30ºE significa 30º hacia el Este contados desde el Sur, lo que equivale a rumbo circular de 150º. | + | {{Tabla3|celda1=<center>[[Imagen:rumbo2.jpg|245px]]{{p}}Fig. 1</center>|celda2=<center>[[Imagen:rumbo3.jpg|260px]]{{p}}Fig. 2</center>|celda3=<center>[[Imagen:rumbo.jpg|265px]]{{p}}Fig. 3</center>}} |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{p}} | + | {{Videotutoriales|titulo=Ángulos horizontales|enunciado= |
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ángulos horizontales | + | |titulo1=Tutorial |
| |duracion=9'37" | |duracion=9'37" | ||
| |sinopsis=Los ángulos y los puntos cardinales. | |sinopsis=Los ángulos y los puntos cardinales. | ||
| Línea 157: | Línea 160: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Problema | + | |titulo1=Problema 1 |
| |duracion=7'58" | |duracion=7'58" | ||
| |sinopsis=Dos ciudades A y B están separadas 50 millas. La ciudad b está situada con respecto a la ciudad A, a 58º sureste. Una tercera ciudad, C, se ve desde A en la dirección S28ºE y desde la ciudad B en la dirección S62ºO. Calcula la distancia en millas entre las ciudades B y C. | |sinopsis=Dos ciudades A y B están separadas 50 millas. La ciudad b está situada con respecto a la ciudad A, a 58º sureste. Una tercera ciudad, C, se ve desde A en la dirección S28ºE y desde la ciudad B en la dirección S62ºO. Calcula la distancia en millas entre las ciudades B y C. | ||
| |url1=https://www.youtube.com/watch?v=aVLEFVd3rY8 | |url1=https://www.youtube.com/watch?v=aVLEFVd3rY8 | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Problema 2 |
| |duracion=17'05" | |duracion=17'05" | ||
| - | |sinopsis=Ejercicios sobre ángulos horizontales (nivel 1). | + | |sinopsis=Problema sobre ángulos horizontales (nivel 1). |
| |url1=https://www.youtube.com/watch?v=h0ZdbUw5b5g | |url1=https://www.youtube.com/watch?v=h0ZdbUw5b5g | ||
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Problema 3 |
| |duracion=25'03" | |duracion=25'03" | ||
| - | |sinopsis=Ejercicios sobre ángulos horizontales (nivel 2). | + | |sinopsis=Problema sobre ángulos horizontales (nivel 2). |
| |url1=https://www.youtube.com/watch?v=p-ofykbNHOg | |url1=https://www.youtube.com/watch?v=p-ofykbNHOg | ||
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Problema 4 |
| |duracion=15'20" | |duracion=15'20" | ||
| - | |sinopsis=Ejercicios sobre ángulos horizontales (nivel 3). | + | |sinopsis=Problema sobre ángulos horizontales (nivel 3). |
| |url1=https://www.youtube.com/watch?v=DojX8RPkLQg | |url1=https://www.youtube.com/watch?v=DojX8RPkLQg | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ángulo
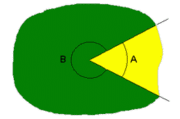
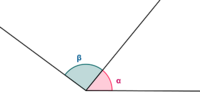
En el dibujo de la derecha puedes ver como dos semirrectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, A y B. Actividad en la que deberás construir un ángulo usando las herramientas de dibujo que se te proporcionan. Ángulos: definición, clasificación y medida. Ángulos: definición, clasificación y medida. Concepto de ángulo. Elementos. Amplitud. Región angular |
Tipos de ángulos
Por su amplitud, distinguimos los siguientes tipos de ángulos:
- Ángulo nulo es aquel definido por dos semirrectas que coinciden. No abarca ninguna porción del plano.
- Ángulo llano es aquel definido por dos semirrectas con la misma dirección, aunque sentidos opuestos. Abarca un semiplano, esto es, la mitad del plano.
- Ángulo convexo es aquel que es menor que un ángulo llano.
- Ángulo cóncavo es aquel que es mayor que un ángulo llano.
- Ángulo recto es aquel ángulo convexo definido por dos semirrectas perpendiculares. Abarca la cuarta parte de un plano.
- Ángulo agudo es aquel que es menor que un ángulo recto.
- Ángulo obtuso es aquel que es mayor que un ángulo recto y menor que un ángulo llano.
- Ángulo completo es aquel que abarca todo el plano.
En esta escena podrás ver una animación con los distintos tipos de ángulos según su abertura.
En este video vamos a ver cómo se clasifican los ángulos según su amplitud: rectos agudos, obtusos, llanos, completos, nulos, convexos y cóncavos.
En este video vamos a clasificar los ángulos según su amplitud de manera dinámica en: nulo, obtuso, llano, cóncavo, convexo, recto y agudo.
En este video vamos a ver la clasificación de los ángulos de acuerdo a sus medidas: ángulo agudo, ángulo recto, ángulo obtuso, ángulo llano, ángulo completo, ángulo entrante o cóncavo, ángulo negativo y ángulo nulo.
Actividad en la que comprobarás tus conocimientos sobre los tipos de ángulos.
Relaciones entre ángulos
|
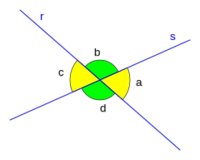
Ángulos complementarios, suplementarios, opuestos por el vértice y formados por rectas secantes.
Con este video vamos a estudiar la clasificación de los ángulos de acuerdo a su relación: ángulos consecutivos, ángulos complementarios, ángulos suplementarios, ángulos conjugados, ángulos opuestos por el vértice y ángulos adyacentes.
Ángulos complementarios y suplementarios. Ejemplos.
Ángulos relacionados según su posición y según su amplitud.
Ángulos consecutivos, complementarios, suplementarios y adyacentes.
Actividad en la que podrás observar las distintas relaciones que hay entre ángulos.
En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice.
Ángulos de lados paralelos o perpendiculares
Proposición
- Dos ángulos cuyos lados son paralelos o son iguales o son suplementarios.
- Dos ángulos cuyos lados son perpendiculares o son iguales o son suplementarios.
En esta escena podrás comprobar que dos ángulos cuyos lados son paralelos o son iguales o son suplementarios .
En esta escena podrás comprobar que dos ángulos cuyos lados son perpendiculares o son iguales o son suplementarios.
Ángulos entre dos paralelas cortadas por una transversal
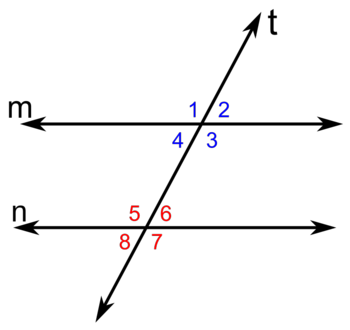
Si una recta transversal corta a dos rectas paralelas:
Propiedades
En esta escena podrás ver los distintos tipos de ángulos que se forman al cortar dos rectas paralelas mediante otra recta transversal. También podrás ver cuando estos ángulos coinciden o son suplementarios. |
Medida de ángulos
La siguiente tanda de videotutoriales condensa todo lo que se va a ver en este apartado:
- Definición de ángulo. Tipos.
- Sistema sexagesimal.
- Definición de radian.
- Equivalencia entre radianes y grados sexagesimales
Relación entre los sistemas de medida sexagesimal, centesimal y radial.
- Concepto de ángulo orientado: ángulos positivos y negativos.
- Sistema sexagesimal, centesimal y radial.
- Ejemplos de conversiones entre sistemas.
Sistema sexagesimal
- Si dividimos el ángulo completo en 360 partes iguales, cada una de ellas decimos que mide un grado sexagesimal. Para indicar que una medida está en grados sexagesimales se acompaña la medida numérica con un superíndice en forma de circulito (º). Así tenemos que:
- El ángulo completo tiene 360º.
- El ángulo llano tiene 180º
- El ángulo recto tiene 90º.
- Un grado sexagesimal se divide en otras unidades más pequeñas llamadas minutos sexageximales. Un grado equivale a 60 minutos (1º=60').
- Un minuto sexagesimal, a su vez, también se divide en otras unidades más pequeñas, llamadas segundos sexagesimales. Un minuto equivale a 60 segundos (1'=60").
El sistema sexagesimal: definición y equivalencias. Ejemplos de conversiones.
Sistema sexagesimal. Paso de forma incompleja a compleja.
Sistema sexagesimal. Paso de forma compleja a incompleja.
Convertir grados (en decimal) a grados, minutos y segundos:
Convierte 63.43º a grados, minutos y segundos.
Convierte 27.312º a grados, minutos y segundos.
Convierte 29.99º a grados, minutos y segundos.
Convierte a grados, minutos y segundos:
a) 15.925º
b) 78.8319º
Convierte a grados, minutos y segundos:
a) 55.0431º
b) 239.8004º
Convertir grados, minutos y segundos a grados (decimal):
Convierte 72º 42' 15" a grados.
Convierte 98º 22' 55" a grados.
Convierte a grados:
a) 94º 45' 15"
b) 163º 28' 42"
Convierte a grados:
a) 78º 56' 11"
b) 287º 5' 9"
Convertir grados, minutos y segundos a minutos (decimal):
Convierte 48º 29' 18" a minutos.
Convierte 7º 7' 7" a minutos.
Convertir grados, minutos y segundos a segundos (decimal):
Convierte 31º 27' 30" a minutos.
Convierte 12º 24' 15" a minutos.
Construye en la escena ángulos de 25º, 135º, 45º, 123º, 180º, 90º, 190º, 0º, 270º, 330º, 360º. Apunta en tu cuaderno de qué tipo es cada uno de ellos.
|
Calculadora: Pasar ángulos con formato decimal a formato "grados, minutos y segundos" y viceversa |
Sistema centesimal
- Si dividimos el ángulo completo en 400 partes iguales, cada una de ellas decimos que mide un grado centesimal. Para indicar que una medida está en grados centesimales se acompaña la medida numérica con la letra g en forma de superíndice. Así tenemos que:
- El ángulo completo tiene 400g.
- El ángulo llano tiene 200g.
- El ángulo recto tiene 100g.
- Un grado centesimal se divide en otras unidades más pequeñas llamadas minutos centesimales. Un grado centesimal equivale a 100 minutos centesimales (100m o 100c).
- Un minuto centesimal, a su vez, también se divide en otras unidades más pequeñas, llamadas segundos centesimales. Un minuto centesimal equivale a 100 segundos centesimales (100s o 100cc).
El sistema centesimal: definición y equivalencias. Ejemplos de conversiones.
El radián
Equivalencia entre radianes y grados sexagesimales
|
|
En consecuencia:

Como la longitud de una circunferencia de radio
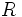 es
es 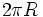 , tenemos que una circunferencia contiene
, tenemos que una circunferencia contiene 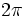 veces a la radio. Por tanto, 360º equivalen a
veces a la radio. Por tanto, 360º equivalen a 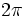 rad y , dividiendo por 2, 180º equivalen a
rad y , dividiendo por 2, 180º equivalen a 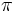 rad.
rad.Utilizando la equivalencia anterior, y mediante una regla de tres, podemos obtener las siguientes equivalencias:
| Grados | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
Equivalencia entre grados sexagesimales y radianes.
El sistema radial o circular. Equivalencias con el sistema sexagesimal.
Ejemplos:
- Expresa el ángulo 32,56º (32 grados y 56 centésimas de grado) en grados, minutos y segundos.
- Expresa el ángulo 46º15'36" en grados sexagesimales.
- Expresa el ángulo 2,6 rad. en grados, minutos y segundos.
- Expresa en radianes el ángulo 72º.
Introducción a los radianes.
Conversión entre radianes y grados. Ejemplos.
Conversión entre radianes y grados. Ejemplos.
Convertir grados sexagesimales a radianes:
Expresa 200º en radianes.
Expresa 135º en radianes.
Expresa 45.32º en radianes.
Expresa 16.142º en radianes.
Expresa 132º 42' 37" en radianes.
Expresa 12º 45" en radianes.
Expresa 750º en radianes.
Expresa 150º y -45º en radianes.
Convertir radianes a grados sexagesimales:
Expresa 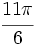 radianes en grados.
radianes en grados.
Expresa 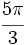 radianes en grados.
radianes en grados.
Expresa 8 radianes en grados.
Expresa 0.5 radianes en grados.
Expresa 5.214 radianes en grados.
Expresa 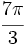 radianes en grados.
radianes en grados.
Expresa 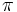 radianes y
radianes y 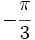 radianes en grados.
radianes en grados.
Otros ejercicios:
Indica en que cuadrante está cada uno de los siguientes ángulos: 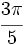 radianes,
radianes, 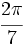 radianes y 3 radianes.
radianes y 3 radianes.
Operaciones con ángulos
Suma
Dos o más ángulos pueden sumarse para formar otro. La operación suma de ángulos se realiza tanto gráficamente como analíticamente:
- La suma gráfica se realiza colocando los ángulos en posición de consecutivos, es decir, compartiendo el vértice y un lado, para dar lugar a otro ángulo que comprende a ambos.
- La suma analítica se realiza sumando las amplitudes de los ángulos para obtener la amplitud del ángulo resultante.
Actividad en la que podrás ver como se suman ángulos gráficamente y de forma analítica en forma simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Construcción gráfica de la suma de dos ángulos, con regla y compás.
Procedimiento
Para sumar analíticamente un ángulos en sexagesimal, en forma compleja:
- Sumamos cada una de las unidades del ángulo (grados, minutos y segundos).
- Si la suma de los segundos es superior a 60, la transformamos en minutos, y se la añadimos a los minutos.
- Si la suma de los minutos es superior a 60, la transformamos en grados, y se la añadimos a los grados.
Ejemplo: Suma de ángulos
Calcula la siguiente suma de ángulo en sexagesimal en forma compleja:
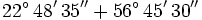
Solución:
Si sumamos por separado los grados, los minutos y los segundos, resulta:
22º 48' 35" + 56º 45' 30" _______________ 78º 93' 65"
Pero 65" equivalen a 1' (60") y 5", luego la suma se puede escribir así:
78º 94' 5"
De la misma forma, 94' equivalen a 1º (60') y 34'. Luego la suma es:
79º 34' 5"
Realiza en tu cuaderno las siguientes sumas de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" + 37º 42' 15"
- b) 125º 15' 30" + 24º 50' 40"
- c) 33º 33' 33" + 17º 43' 34"
Suma de ángulos en sexagesimal.
Suma de ángulos en forma compleja.
Calcula: (26º 42' 51") + (11º 30' 14")
Calcula: (26º 14' 41") + (24º 59")
Calcula: (38º 47') + (19º 54' 10")
Resta
La resta o diferencia de ángulos puede hacerse, igual que la suma, de dos formas: gráfica y analítica.
- La resta gráfica, consiste en colocar los dos ángulos de manera que compartan el vértice y un lado. Así, el ángulo mayor comprende al menor, y el exceso es la diferencia entre ambos.
- La resta analítica se realiza restando la amplitud del ángulo menor de la del mayor.
Actividad en la que podrás ver como se restan ángulos de forma gráfica y de forma analítica simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Construcción gráfica de la resta de dos ángulos, con regla y compás.
Procedimiento
Para restar analíticamente ángulos en sexagesimal, en forma compleja:
- Restamos cada una de las unidades del ángulo (grados, minutos y segundos).
- Si al restar los segundos, el minuendo es menor que el sustraendo, transformaremos un minuto en 60" y se lo sumaremos a los segundos.
- Si al restar los minutos, el minuendo es menor que el sustraendo, transformaremos un grado en 60' y se lo sumaremos a los minutos.
- Terminaremos restando los grados normalmente.
Veamos un ejemplo:
Ejemplo: Resta de ángulos
Calcula la siguiente resta de ángulo en sexagesimal en forma compleja :
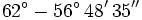
Debemos hacer la siguiente operación:
62º 0' 0" − 56º 48' 35" _______________
Igual que en la suma, deberíamos restar por separado las horas los minutos y los segundos, pero no podemos hacer las restas 0-35 (segundos) ni 0-48 (minutos). Para conseguirlo transformamos una grado en 60 minutos y un minuto en 60 segundos. Es decir, los 60º se convierten en 61º 59' 60".
61º 59' 60" − 56º 48' 35" _____________ 5º 11' 25"
Realiza en tu cuaderno las siguientes restas de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" - 37º 42' 15"
- b) 125º 15' 30" - 24º 50' 40"
- c) 33º 33' 33" - 17º 43' 34"
Calcula el complementario y el suplementario de los siguientes ángulos y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40"
- b) 37º 42' 15"
- c) 125º 15' 30"
Resta de ángulos en sexagesimal.
Resta de ángulos en sexagesimal.
Cálculo del complementario y del suplementario.
Cálculo del complementario y del suplementario.
Resta de ángulos en forma compleja.
Calcula: (213º 17' 25") - (122º 35' 48")
Calcula: (49º 12') - (15º 27' 50")
Calcula: (100º 18") - (31º 20' 10")
Calcula: (147º) - (23º 52' 3")
¿Cuál es el complementario de 53º41'28"
¿Cuál es el suplementario de 75º16'49"
Calcula: (131º 45' 36") - (31º 58' 26")
Suma y resta de ángulos en forma compleja, en el sistema sexagesimal.
Suma y resta de ángulos en forma compleja, en el sistema sexagesimal.
Multiplicación por un número natural
Multiplicar un ángulo por un número natural equivale a sumar el ángulo consigo mismo tantas veces como indique el número.
- La multiplicación gráfica de un ángulo por un número natural se hace colocando el ángulo en posición de consecutivo consigo mismo tantas veces como indique el número.
- La multiplicación analítica se realiza multiplicando el número por la amplitud del ángulo.
Actividad en la que podrás ver como se multiplican ángulos por números naturales de forma gráfica y de forma analítica en forma simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Procedimiento
Para multiplicar analíticamente un ángulo en sexagesimal, en forma compleja, por un número natural:
- Multiplicamos por ese número cada una de las unidades del ángulo (grados, minutos y segundos).
- Si los segundos resultantes son superiores a 60, los transformamos en minutos, y se lo añadimos a los minutos.
- Si los minutos resultantes son superiores a 60, los transformamos en grados, y se lo añadimos a los grados.
Veamos un ejemplo:
Ejemplo: Multiplicación de un ángulo por un número
Calcula la siguiente multiplicación de un ángulo en sexagesimal en forma compleja por un número natural:
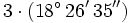
18º 26' 35" x 3 _______________ 54º 78' 105"
Pero 105" = 1' 45", luego
54º 79' 45"
Pero 79' = 1º 19', luego
55º 19' 45"
Realiza en tu cuaderno las siguientes multiplicaciones de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" x 2
- b) 37º 42' 15" x 4
- c) 125º 15' 30" x 3
Multiplicación de ángulos por un número en forma compleja en sexagesimal.
Calcula: (25º 12' 37")· 5
Calcula: (50º 18")· 20
Calcula: (72º 31')· 17
División por un número natural
La división de un ángulo por un número natural es una operación que consiste en separar el ángulo en tantas partes iguales como nos indique el número.
- La división se realiza de forma analítica dividiendo la amplitud del ángulo entre el número natural correspondiente.
- La división gráfica resulta más compleja ya que no siempre se puede hacer con regla y compás.
Por ejemplo, la división de un ángulo en tres partes iguales (el famoso problema de la trisección del ángulo), es imposible para la mayor parte de los ángulos. En cambio, siempre es posible calcular la división de un ángulo en dos partes iguales gráficamente, mediante el trazado de la bisectriz del ángulo.
Construcción gráfica de la trisección de un ángulo recto, con regla y compás.
Actividad en la que podrás ver como se dividen ángulos por números naturales. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Procedimiento
Para dividir analíticamente un ángulo en sexagesimal, en forma compleja, entre un número natural:
- Dividimos los grados entre ese número.
- Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos.
- Dividimos los minutos.
- Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. #Dividimos los segundos.
Veamos un ejemplo:
Ejemplo: División por un número en forma compleja
Calcula la siguiente división de un ángulo en sexagesimal en forma compleja entre un número natural:
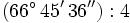
Realiza en tu cuaderno las siguientes divisiones de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" : 5
- b) 37º 42' 15" : 4
- c) 125º 15' 30" : 3
División de un ángulo entre un número en forma compleja en sexagesimal.
Calcula: (139º 34' 48") : 6
Calcula: (50º 20' 26") : 12
Calcula: (125º 37') : 9
Calcula: (65º 21') : 3
Multiplicación y división en forma compleja, en el sistema sexagesimal.
Actividades
3 ejercicios sobre medida y tipos de ángulos.
- Actividad en la que podrás ver como se suman, restan, multiplican o dividen ángulos en sexagesimal, en forma compleja.
- Ejercicios resueltos.
Ejercicios resueltos sobre operaciones con ángulos en sexagesimal.
Ejercicios de autoevaluación sobre operaciones con ángulos en sexagesimal.
En esta escena podrás ver como se opera con ángulos gráficamente y analíticamente.
Ángulos en los polígonos
Ángulos interiores y exteriores
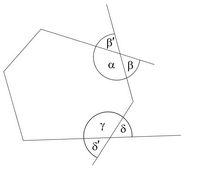
En el dibujo de la derecha, el ángulo |
Polígonos cóncavos y convexos
- Un polígono es convexo si todos sus ángulos interiores miden menos de 180º.
- Un polígono es cóncavo si alguno de sus ángulos interiores mide más de 180º.
Ángulos en un triángulo
Propiedad
Los tres ángulos interiores de un triángulo suman 180º.
Demostración de que la suma de los ángulos de un triángulo es un ángulo llano (180º).
En esta escena podrás ver como se obtiene la suma de los ángulos triángulo.
Ejemplos que ilustran la propiedad de que la suma de los ángulos internos de un triángulo es 180º.
Los ángulos de un triángulo miden 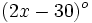 ,
, 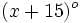 y
y 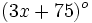 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un cuadrilátero
Propiedad
Los cuatro ángulos interiores de un cuadrilátero suman 360º.
En la siguiente escena de Geogebra.
En esta escena podrás ver como se calcula la suma de los ángulos interiores de un cuadrilátero.
Halla el ángulo que falta en los siguientes cuadriláteros.
Halla los ángulos que faltan en los siguientes cuadriláteros.
Halla el ángulo que falta en el siguiente cuadrilátero.
Los ángulos de un cuadrilátero miden 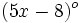 ,
, 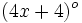 ,
, 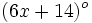 y
y 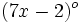 . Determina el valor de dichos ángulos.
. Determina el valor de dichos ángulos.
Ángulos en un polígono de n lados
Propiedades
- La suma de los ángulos interiores de un polígono de
 lados es igual a
lados es igual a 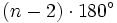 .
.
- Si el polígono de
 lados es regular:
lados es regular:
- Cada ángulo interior mide
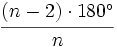 .
.
- Cada ángulo exterior mide
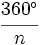 .
.
- Cada ángulo interior mide
- Desde un vértice cualquiera del polígono se pueden trazar n-3 diagonales que dividen al polígono en n-2 triángulos. Sumando los ángulos de todos esos triángulos se obtiene la fórmula, ya que la suma de los ángulos de cada triángulo es 180º.
- Si además el polígono es regular:
- Al tener todos sus ángulos interiores iguales, cada uno de ellos se obtendrá dividiendo el valor del primer apartado por el número de lados, n.
- Para ver la medida del ángulo exterior restaremos a 180º el ángulo interior:
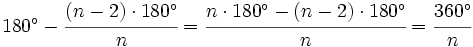
- Deducción de la fórmula de la suma de los ángulos interiores de un polígono cualquiera.
- Ejemplos de aplicación.
- Deducción de la fórmula para hallar la medida de los ángulos interiores de un polígono regular.
Deducción de la fórmula de la suma de los ángulos interiores de un polígono de n lados.
Suma de los ángulos interiores de un polígono.
- Suma de los ángulos interiores de un triángulo.
- Cálculo de los ángulos interiores de un polígono regular y de su suma.
Ángulos interiores de un cuadrado y de un hexágono regular.
¿Existe un polígono convexo cuyos ángulos sumen 1440º? Indica su nombre y la cantidad de lados que tiene.
Ángulo exterior de un polígono regular
Actividades
Ejercicios de autoevaluación sobre los ángulos en los polígonos.
Ejercicios de autoevaluación sobre los ángulos en los polígonos.
Ángulos en la circunferencia
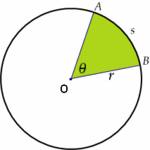
Ángulo central
En esta actividad podrás ver cómo es un ángulo central y el arco de circunferencia que determina.
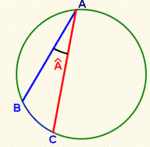
Ángulo inscrito
Propiedades
Propiedades
- Dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
- La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- Todo ángulo inscrito en una semicircunferencia es recto.
Las dos primeras propiedades se pueden comprobar (no es una demostración) en la siguiente escena:
En esta escena podrás comprobar la relación que hay entre ángulos centrales y ángulos inscritos en una circunferencia.
La tercera propiedad la puedes comprobar en esta otra escena:
En esta escena podrás comprobar qué propiedad tienen todos los ángulos inscritos en una semicircunferencia.
En esta actividad podrás ver cómo es un ángulo inscrito y su relación con el ángulo central correspondiente.
En esta actividad podrás ver cómo un ángulo inscrito en una semicircunferencia es recto.
Actividades y videotutoriales
Ángulos centrales e incritos. Propiedad.
Aplicación de las propiedades de los ángulos inscritos a problemas de cuerdas que se cortan en una circunferencia.
Aplicación de las propiedades de los ángulos inscritos a problemas de cuerdas que se cortan en una circunferencia.
Ejercicios de autoevaluación sobre ángulos centrales e inscritos.
Ángulos en una circunferencia: Interior, central, inscrito, semiinscrito, interior y circunscrito.
En esta escena podrás ver los distintos tipos de ángulos que puede haber en una circunferencia: central, inscrito, semiinscrito, circunscrito, interior, exterior.
En esta escena podrás practicar el cálculo del valor de distintos tipos de ángulos en una circunferencia.
Ángulos horizontales
Angulos horizontales son los ángulos que se encuentran contenidos en el plano horizontal. Su medida se realiza con respecto al meridiano terrestre en el cual nos encontremos situados.
Puntos cardinales
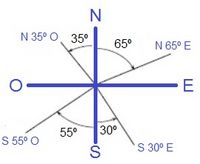
Los puntos cardinales son los cuatro sentidos que conforman un sistema de referencia cartesiano para representar la orientación en un mapa o en la propia superficie terrestre. Son los siguientes: Este (E), Oeste (O), Norte (N) y Sur (S).
Esta composición genera cuatro ángulos de noventa grados que a su vez se dividen por las bisectrices, generando Noroeste (NE), Suroeste (SE), Noreste (NE) y Sureste (SE). Si seguimos subdividiendo, obtenemos 8 direcciones terciarias: Nor-noroeste (NNO); Nor-noroeste (NNO); Sur-sureste (SSE); Sur-suroeste (SSO); Este-noreste (ENE); Este-sureste (ESE); Oeste-noroeste (ONO) y Oeste-suroeste (OSO), obteniendose la rosa de los vientos que es usada en navegación desde siglos ancestrales, y que tienes representada en la imagen de la derecha. |
La palabra cardinal se deriva del nombre latino «cardo», que identificaba, en las ciudades romanas, la calle trazada de norte a sur y que pasaba por el centro de la ciudad. Esto significa que el único punto verdaderamente cardinal, al menos desde el punto de vista etimológico, debería ser el Norte, y, en menor grado, el Sur.
Por eso se usa la expresión «de una importancia cardinal» cuando se quiere resaltar esa importancia. De los puntos cardinales, es el Norte el que identifica la dirección de la orientación, por lo que suele decirse en sentido figurado que una persona ha perdido su Norte cuando se encuentra desorientada o ha perdido su rumbo.
Rumbo
El rumbo es la dirección en la que nos movemos o navegamos, o en la cual nos dirigimos o miramos. Hay dos tipos:
En navegación, anteriormente, el rumbo se expresaba en "cuadrantal", por referencia a un cuadrante de la rosa náutica, pero actualmente se utiliza el rumbo "circular". |
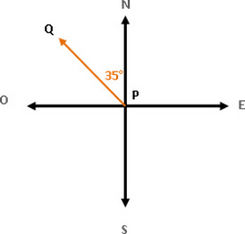
Ejemplo 1: Para ir de P a Q podemos decir que el rumbo es N35°O, o bien que Q está "35° al oeste del norte" de P. (Ver Fig. 1)
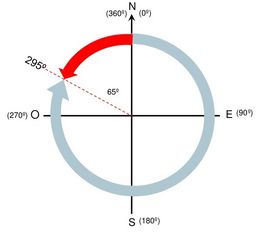
Ejemplo 2: Un rumbo cuadrantal N65ºO significa 65º hacia el Oeste contados desde el Norte, lo que equivale a un rumbo circular de 295º. (Ver Fig. 2)
Ejemplo 3: Un rumbo cuadrantal N35ºE significa 35º hacia el Este contados desde el Norte. En este caso coincide con el rumbo circular. (Ver Fig. 3)
Los ángulos y los puntos cardinales.
Dos ciudades A y B están separadas 50 millas. La ciudad b está situada con respecto a la ciudad A, a 58º sureste. Una tercera ciudad, C, se ve desde A en la dirección S28ºE y desde la ciudad B en la dirección S62ºO. Calcula la distancia en millas entre las ciudades B y C.
Problema sobre ángulos horizontales (nivel 1).
Problema sobre ángulos horizontales (nivel 2).
Problema sobre ángulos horizontales (nivel 3).
Ejercicios
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
Problemas sobre ángulos.
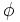 mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
mide un radián porque abarca un arco que mide igual que el radio de la circunferencia.
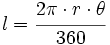
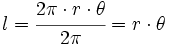
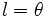
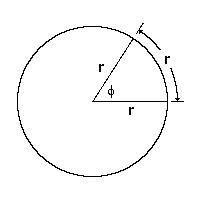
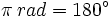
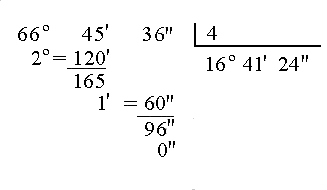
 es interno y los ángulos
es interno y los ángulos 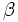 y
y 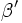 son sus correspondientes ángulos externos.
son sus correspondientes ángulos externos.
 y su arco correspondiente AB.
y su arco correspondiente AB.
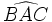 .
.