Plantilla:Función inversa (1ºBach)
De Wikipedia
| Revisión de 10:09 13 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Funciones trigonométricas recíprocas o funciones arco) |
||
| Línea 9: | Línea 9: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | Sea <math>f\;</math> una función real [[Función inyectiva|inyectiva]], cuyo dominio sea el conjunto <math>X\;</math> y cuya imagen sea el conjunto <math>Y\;</math>. Entonces, la '''función recíproca o inversa''' de <math>f\;</math>, denotada <math>f^{-1}\;</math>, es la función de dominio <math>Y\;</math> e imagen <math>X\;</math> definida por la siguiente regla: | + | Sea <math>f\;</math> una función real [[Función inyectiva|inyectiva]], cuyo dominio sea el conjunto <math>X\;</math> y cuya imagen sea el conjunto <math>Y\;</math> (en tal caso <math>f:X \rightarrow Y</math> es [[Función biyectiva|biyectiva]]). Entonces, la '''función recíproca o inversa''' de <math>f\;</math>, denotada <math>f^{-1}\;</math>, es la función de dominio <math>Y\;</math> e imagen <math>X\;</math> definida por la siguiente regla: |
| - | <center><math>f(x) = y\Leftrightarrow{}f^{-1}(y) = x \,\!</math></center> | + | <center><math>f^{-1}(y) = x \Leftrightarrow{}f(x) = y \,\!</math></center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Propiedades | + | {{Video_enlace_khan |
| + | |titulo1=Comprendiendo las funciones inversas | ||
| + | |duracion=6'11" | ||
| + | |sinopsis=Introducción a las funciones inversas. | ||
| + | |url1=https://www.youtube.com/watch?v=fD5K29ds-Zw | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Propiedades | ||
| |enunciado=Sea <math>f \colon X \rightarrow Y</math> una función y <math>f^{-1}\;</math> su inversa: | |enunciado=Sea <math>f \colon X \rightarrow Y</math> una función y <math>f^{-1}\;</math> su inversa: | ||
| {{p}} | {{p}} | ||
| Línea 24: | Línea 31: | ||
| donde <math>I_X\;</math> e <math>I_Y\;</math> son las [[Función identidad|funciones identidad]] en <math>X\;</math> e <math>Y\;</math> respectivamente. | donde <math>I_X\;</math> e <math>I_Y\;</math> son las [[Función identidad|funciones identidad]] en <math>X\;</math> e <math>Y\;</math> respectivamente. | ||
| - | |demo= | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Función inversa''|cuerpo= | + | ==Obtención de la expresión analítica de la función inversa== |
| - | {{ai_cuerpo | + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= |
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> y de su inversa <math>f^{-1}(x)\;</math>. | + | Para intentar hallar la expresión analítica de la inversa de y=f(x): |
| - | |actividad= | + | |
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^3\;</math> (en verde) y la de <math>f^{-1}(x)=\sqrt[3]{x}</math> (en amarillo). Observa que son simétricas respecto de la bisectriz del primer cuadrante, la recta <math>y=x\;</math> (en rojo). | + | |
| + | #Se despeja (si se puede) la variable "x" para ponerla en función de la variable "y". | ||
| + | #Se intercambian las dos incógnitas (donde aparece "x" se pone "y" y viceversa). | ||
| + | #La expresión resultante es la de la función inversa de f. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| - | <center><iframe> | + | {{Videotutoriales|titulo=Obtención de la expresión analítica de la función inversa|enunciado= |
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4f.html | + | {{Video_enlace_khan |
| - | width=450 | + | |titulo1=Ejemplo 1 |
| - | height=380 | + | |duracion=11'55" |
| - | name=myframe | + | |sinopsis=1 ejemplo sobre el cáculo de la función inversa y su interpretación gráfica. |
| - | </iframe></center> | + | |url1=https://www.youtube.com/watch?v=zdQr2IWmtfw |
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4f.html '''Click''' aquí si no se ve bien la escena]</center> | + | }} |
| - | + | {{p}} | |
| - | Prueba a cambiar también la función <math>f(x)=x^3\;</math> por otras funciones, por ejemplo, <math>f(x)=x^2\;</math>. ¿Quien sería su función inversa?. ¿Que ocurre?. Recuerda que para que una función tenga inversa debe ser [[Función inyectiva |inyectiva]]. | + | {{Video_enlace_khan |
| - | + | |titulo1=Ejemplos 2 | |
| - | No olvides pulsar "Intro" al cambiar cada función. | + | |duracion=6'53" |
| + | |sinopsis=2 ejemplos sobre el cáculo de la función inversa y su interpretación gráfica. | ||
| + | |url1=https://www.youtube.com/watch?v=4QOo3Y1p8eM | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Ejemplos 3 | ||
| + | |duracion=13'30" | ||
| + | |sinopsis=Algunos ejemplos sobre el cálculo de la función inversa y sobre la composición de funciones. | ||
| + | |url1=http://www.unicoos.com/clase/matematicas/1-bachiller/funciones/composicion-de-funciones/composicion-de-funciones-y-funcion-inversa | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 4 | ||
| + | |duracion=8'22" | ||
| + | |sinopsis=Obtención de la función inversa de <math>f(x)=\cfrac{2x+3}{5-x}\;</math> previa demostración de su inyectividad. | ||
| + | |url1=https://www.youtube.com/watch?v=TxRpKrQJsdw | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejemplo 5 | ||
| + | |duracion=14'07" | ||
| + | |sinopsis=1 ejemplo sobre el cálculo de la función inversa de una función trigonométrica. | ||
| + | |url1=https://www.youtube.com/watch?v=3ivTz5obhj4 | ||
| }} | }} | ||
| }} | }} | ||
| Línea 52: | Línea 82: | ||
| |enunciado=Halla la función inversa de la función <math>f:\mathbb{R}\to\mathbb{R}</math> definida por <math>f(x)=x^2\;</math>: | |enunciado=Halla la función inversa de la función <math>f:\mathbb{R}\to\mathbb{R}</math> definida por <math>f(x)=x^2\;</math>: | ||
| |sol= | |sol= | ||
| - | Como la función <math>f(x)=x^2\;</math> no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y alos que si podamos calcular su inversa: | + | Como la función <math>f(x)=x^2\;</math> no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y a los que si podamos calcular su inversa: |
| <center><math>f(x)=x^2= | <center><math>f(x)=x^2= | ||
| Línea 73: | Línea 103: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4g.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4g.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás introducir la expresión analítica de una función y obtener la expresión analítica de su inversa, así como ver sus respectivas representaciones gráficas. También se te propondrán algunas actividades. | ||
| + | |enlace=[https://ggbm.at/tWDeFVRJ Función inversa o recíproca] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=Obtención del rango o recorrido de una función. | ||
| + | |duracion=9'33" | ||
| + | |sinopsis=Ejemplo sobre el cálculo del rango o recorrido de una función mediante el cálculo del dominio de su función inversa. | ||
| + | |url1=http://www.unicoos.com/video/matematicas/1-bachiller/funciones/funcion-inversa/rango-recorrido-o-imagen-de-una-funcion | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Función inversa o recíproca
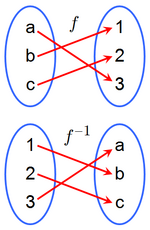
Si  es una función que lleva elementos de es una función que lleva elementos de 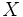 en elementos de en elementos de 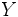 , en ciertas condiciones será posible definir la aplicación , en ciertas condiciones será posible definir la aplicación 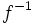 que realice el camino de vuelta de que realice el camino de vuelta de 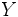 a a 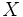 . En ese caso diremos que . En ese caso diremos que 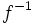 es la función inversa o recíproca de es la función inversa o recíproca de  . Formalmente: . Formalmente:
Introducción a las funciones inversas. Propiedades Sea
donde |
Obtención de la expresión analítica de la función inversa
Procedimiento
Para intentar hallar la expresión analítica de la inversa de y=f(x):
- Se despeja (si se puede) la variable "x" para ponerla en función de la variable "y".
- Se intercambian las dos incógnitas (donde aparece "x" se pone "y" y viceversa).
- La expresión resultante es la de la función inversa de f.
1 ejemplo sobre el cáculo de la función inversa y su interpretación gráfica.
2 ejemplos sobre el cáculo de la función inversa y su interpretación gráfica.
Algunos ejemplos sobre el cálculo de la función inversa y sobre la composición de funciones.
Obtención de la función inversa de 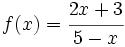 previa demostración de su inyectividad.
previa demostración de su inyectividad.
1 ejemplo sobre el cálculo de la función inversa de una función trigonométrica.
Ejemplo: Función inversa
Halla la función inversa de la función 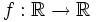 definida por
definida por  :
:
Como la función  no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y a los que si podamos calcular su inversa:
no es inyectiva, no podemos calcular su inversa. No obstante, podemos descomponerla en dos trozos que si sean funciones inyectivas por separado y a los que si podamos calcular su inversa:
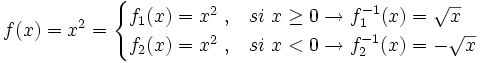
En la siguiente escena puedes ver  (en verde),
(en verde), 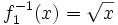 (en amarillo), y
(en amarillo), y 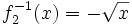 (en turquesa):
(en turquesa):
En esta escena podrás introducir la expresión analítica de una función y obtener la expresión analítica de su inversa, así como ver sus respectivas representaciones gráficas. También se te propondrán algunas actividades.
Ejemplo sobre el cálculo del rango o recorrido de una función mediante el cálculo del dominio de su función inversa.
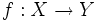 es
es 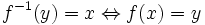
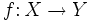 una función y
una función y 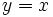 .
.
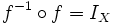

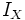 e
e 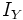 son las
son las