Sistemas de ecuaciones de primer grado
De Wikipedia
| Revisión de 17:04 5 jul 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:46 5 jul 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Ecuación== | + | ==Ecuación de primer grado con dos incógnitas== |
| - | {{Caja_Amarilla|texto=Una '''ecuación''' es una igualdad entre expresiones algebraicas, en las que aparece una o más letras, llamadas incógnitas.{{p}} | + | {{Caja_Amarilla|texto=Una '''ecuación de primer grado con dos incógnitas''' es aquella que se puede expresar de la forma: |
| - | Una '''solución''' de una ecuación son los números que hacen que la igualdad sea cierta, al sustituir las incógnitas por dichos números.{{p}} | + | <center><math>ax+by=c\;\!</math></center> |
| - | Podemos tener ecuaciones con una incógnita, con dos incógnitas, etc.{{p}} | + | donde <math>x\;\!</math> e <math>y\;\!</math> son variables y <math>a,\ b,\;\!</math> y <math>c\;\!</math> constantes. |
| }} | }} | ||
| - | '''Ejemplos:''' | ||
| - | *Ecuación con una incógnita: <math>x^2+1=x-3\;\!</math>. | ||
| - | *Ecuación con dos incógnitas: <math>x-2y=x^2+5\;\!</math>. | ||
| {{p}} | {{p}} | ||
| - | ==Ecuación de primer grado== | + | '''Ejemplo: '''<math>x-2y=1\;\!</math> |
| - | {{Caja_Amarilla|texto=Una '''ecuación de primer grado''' es aquella en la que las incognitas no están elevadas a ninguna potencia.{{p}} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | ===Soluciones de una ecuación de primer grado con dos incógnitas=== | ||
| + | Una ecuación de primer grado con dos incógnitas tiene infinitas soluciones. Para cada valor que le asignemos a la variable <math>x\;\!</math>, podemos encontrar un valor de la variable <math>y\;\!</math> despejándola en la ecuación. | ||
| - | '''Ejemplos:''' | + | {{Ejemplo|titulo=Ejemplo: ''Ecuación de primer grado con dos incógnitas'' |
| - | *Ecuación de primer grado con una incógnita: <math>3x-2=x+1\;\!</math>. | + | |enunciado= |
| - | *Ecuación de primer grado con dos incógnitas: <math>x-2=y+1\;\!</math> | + | :Halla algunas soluciones para la ecuación: |
| + | <center><math>3x+y=5\;\!</math></center> | ||
| + | |sol= | ||
| + | Despejamos la variable y: | ||
| + | <center><math>y=5-3x\;\!</math></center> | ||
| + | Construimos una tabla de valores, dandole valores a <math>x\;\!</math> y calculando <math>y\;\!</math> en la expresión anterior: | ||
| + | <table border=1 align=center> | ||
| + | <tr align=center> | ||
| + | <td>'''x'''</td> | ||
| + | <td>0</td> | ||
| + | <td>1</td> | ||
| + | <td>2</td> | ||
| + | <td>...</td> | ||
| + | </tr> | ||
| + | <tr align=center> | ||
| + | <td>'''y'''</td> | ||
| + | <td>5</td> | ||
| + | <td>2</td> | ||
| + | <td>-1</td> | ||
| + | <td>...</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | Las soluciones vienen dadas por las parejas <math>(x,y)\;\!</math> así obtenidas: | ||
| + | <center><math>(0,5),\ (1,2),\ (2,-1),...</math></center> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Toda '''ecuación de primer grado con una incógnita''' se puede reducir a la forma: | Toda '''ecuación de primer grado con una incógnita''' se puede reducir a la forma: | ||
Revisión de 17:46 5 jul 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas es aquella que se puede expresar de la forma:
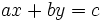
donde  e
e  son variables y
son variables y 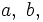 y
y  constantes.
constantes.
Ejemplo: 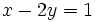
Soluciones de una ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas tiene infinitas soluciones. Para cada valor que le asignemos a la variable  , podemos encontrar un valor de la variable
, podemos encontrar un valor de la variable  despejándola en la ecuación.
despejándola en la ecuación.
Ejemplo: Ecuación de primer grado con dos incógnitas
- Halla algunas soluciones para la ecuación:

Despejamos la variable y:

Construimos una tabla de valores, dandole valores a  y calculando
y calculando  en la expresión anterior:
en la expresión anterior:
| x | 0 | 1 | 2 | ... |
| y | 5 | 2 | -1 | ... |
Las soluciones vienen dadas por las parejas 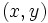 así obtenidas:
así obtenidas:
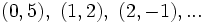
Toda ecuación de primer grado con una incógnita se puede reducir a la forma:
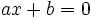
Si 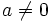 , la ecuación tiene como única solución:
, la ecuación tiene como única solución: 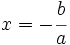 .
.
|
Actividad Interactiva: Solución de una ecuación de primer grado con una incógnita
Actividad 1: Ejemplos de soluciones de ecuaciones de primer grado con una incógnita.
Actividad: Pulsa los botones para ver más ecuaciones. |
Ecuaciones equivalentes
Dos ecuaciones son equivalentes si tienen la misma solución.
Transformaciones que mantienen la equivalencia de las ecuaciones
- Sumar o restar la misma expresión en los dos miembros de la igualdad. Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.
- Multiplicar o dividir los dos miembros de la igualdad por un mismo número distinto de cero. Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.
Resolución de ecuaciones de primer grado
Para resolver una ecuación, hay que transformarla en otras ecuaciones equivalentes, cada vez más sencillas, hasta conseguir despejar la incógnita. Usaremos las transformaciones descritas en el apartado anterior.
|
Actividad Interactiva: Resolución de ecuaciones de primer grado
Actividad 1: Ecuaciones de primer grado sencillas (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones.
Actividad 2: Ecuaciones de primer grado con paréntesis (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones.
Actividad 3: Ecuaciones de primer grado con denominadores (resueltas).
Actividad: Pulsa el botón EJEMPLO para ver más ecuaciones. |
Resolución de problemas mediante ecuaciones de primer grado
Para resolver un problema mediante una ecuación, hay que seguir los siguientes pasos:
- Determinar la incógnita.
- Expresar el enunciado del problema en lenguaje algebraico, es decir, escribir una ecuación en la que intervenga la incógnita.
- Resolver la ecuación, es decir, halla el valor de la incógnita.
- Dar la solución del problema, a partir del valor obtenido de la incógnita.
|
Actividad Interactiva: Resolución de problemas mediante ecuaciones de primer grado
Actividad 1: Problemas resueltos.
Actividad: Pulsa el botón EJEMPLO para ver más problemas. Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes. |

