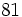Plantilla:Raíces
De Wikipedia
| Revisión de 14:19 31 dic 2017 Coordinador (Discusión | contribuciones) (→La raíz como potencia de exponente fraccionario) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Raíces exactas e inexactas) |
||
| Línea 49: | Línea 49: | ||
| |duracion=5´32" | |duracion=5´32" | ||
| |sinopsis=Potencia de exponente fraccionario. Ejemplos. | |sinopsis=Potencia de exponente fraccionario. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=H1mFjBwx7co | + | |url1=http://www.youtube.com/watch?v=H1mFjBwx7co |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 55: | Línea 55: | ||
| |duracion=7´34" | |duracion=7´34" | ||
| |sinopsis=Potencia de exponente fraccionario. Ejemplos. | |sinopsis=Potencia de exponente fraccionario. Ejemplos. | ||
| - | |url1=https://youtu.be/cVUw0i4q_cg | + | |url1=http://youtu.be/cVUw0i4q_cg |
| }} | }} | ||
| ---- | ---- | ||
| Línea 65: | Línea 65: | ||
| :b) <math>\sqrt[6]{g^5}</math> | :b) <math>\sqrt[6]{g^5}</math> | ||
| :c) <math>\cfrac{1}{\sqrt[7]{x}}</math> | :c) <math>\cfrac{1}{\sqrt[7]{x}}</math> | ||
| - | |url1=https://youtu.be/C0BLyYgc6FI | + | |url1=http://youtu.be/C0BLyYgc6FI |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 74: | Línea 74: | ||
| :<math>3^a=\sqrt[5]{3^2}</math> | :<math>3^a=\sqrt[5]{3^2}</math> | ||
| - | |url1=https://youtu.be/sWUleR_dX5g | + | |url1=http://youtu.be/sWUleR_dX5g |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 83: | Línea 83: | ||
| :<math>\cfrac{m^{\frac{7}{9}}}{m^{\frac{1}{3}}}=m^{\frac{k}{9}} \ \ (m>0)</math> | :<math>\cfrac{m^{\frac{7}{9}}}{m^{\frac{1}{3}}}=m^{\frac{k}{9}} \ \ (m>0)</math> | ||
| - | |url1=https://youtu.be/xTbWL4oFYgA | + | |url1=http://youtu.be/xTbWL4oFYgA |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 92: | Línea 92: | ||
| :<math>\left(r^{\frac{2}{3}} s^3\right)^2 \cdot \sqrt{20\,r^4s^5}</math> | :<math>\left(r^{\frac{2}{3}} s^3\right)^2 \cdot \sqrt{20\,r^4s^5}</math> | ||
| - | |url1=https://youtu.be/Dy2UewBY1pc | + | |url1=http://youtu.be/Dy2UewBY1pc |
| }} | }} | ||
| }} | }} | ||
| Línea 157: | Línea 157: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_descartes|titulo1=La raíz como potencia de exponente fraccionario. Propiedades | + | {{Videotutoriales|titulo=Propiedades de las potencias de exponente fraccionario|enunciado= |
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=9'35" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :a) <math>64^{\frac{1}{3}}</math> | ||
| + | |||
| + | :b) <math>64^{\frac{2}{3}}</math> | ||
| + | |||
| + | :c) <math>\left(\cfrac{8}{27}\right)^{-\frac{2}{3}}</math> | ||
| + | |||
| + | |url1=http://youtu.be/4MPL_lTuG4Y | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=3'03" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :a) <math>9^{\frac{1}{2}}</math> | ||
| + | |||
| + | :b) <math>9^{-\frac{1}{2}}</math> | ||
| + | |||
| + | :c) <math>(-27)^{-\frac{1}{3}}</math> | ||
| + | |||
| + | |url1=http://youtu.be/goAeDI09ndY | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=5'40" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :a) <math>\left(\cfrac{25}{9}\right)^{\frac{1}{2}}</math> | ||
| + | |||
| + | :b) <math>\left(\cfrac{81}{256}\right)^{-\frac{1}{4}}</math> | ||
| + | |||
| + | |url1=http://youtu.be/i0NDAMAwl4o | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=5'36" | ||
| + | |sinopsis=Calcula: | ||
| + | |||
| + | :<math>\cfrac{256^{\frac{4}{7}}}{2^{\frac{4}{7}}}</math> | ||
| + | |||
| + | |url1=http://youtu.be/E0ER5ajLEHA | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=2'50" | ||
| + | |sinopsis=Simplifica: | ||
| + | |||
| + | :<math>6^{\frac{1}{2}} \cdot \left(\sqrt[5]{6}\right)^3</math> | ||
| + | |||
| + | |url1=http://youtu.be/6a9wv6js7Zw | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Propiedades de las potencias de exponente fraccionario|enunciado= | ||
| + | {{AI_descartes | ||
| + | |titulo1=Actividad | ||
| |descripcion=Actividades para que aprendas a operar con raíces expresadas en forma de potencias de exponente fraccionario y a utilizar sus propiedades. | |descripcion=Actividades para que aprendas a operar con raíces expresadas en forma de potencias de exponente fraccionario y a utilizar sus propiedades. | ||
| |url1=http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias33.htm | |url1=http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias33.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación | ||
| + | |descripcion=Simplifica expresiones radicales | ||
| + | |url1=http://es.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-rational-exp-eval/e/simplify-radicals-and-exponentials | ||
| + | }} | ||
| }} | }} | ||
| Línea 166: | Línea 231: | ||
| Se llaman '''raíces exactas''' de un número a aquellas que dan como resultado un número racional. En caso contrario diremos que son '''inexactas''' y el resultado será un número irracional. | Se llaman '''raíces exactas''' de un número a aquellas que dan como resultado un número racional. En caso contrario diremos que son '''inexactas''' y el resultado será un número irracional. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Raíces exactas e inexactas | ||
| - | |duracion=6´29" | ||
| - | |sinopsis=Tutorial que explica las raíces exactas e inexactas y pone ejemplos de ambas. | ||
| - | |url1=https://www.youtube.com/watch?v=QZlZAtIxtCo | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Raíces exactas e inexactas|enunciado= | {{Teorema_sin_demo|titulo=Raíces exactas e inexactas|enunciado= | ||
| Línea 205: | Línea 263: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ejercicios: ''Raíces exactas''|enunciado= | + | {{Videotutoriales|titulo=Raíces exactas e inexactas|enunciado= |
| + | {{Video_enlace | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=6´29" | ||
| + | |sinopsis=Tutorial que explica las raíces exactas e inexactas y pone ejemplos de ambas. | ||
| + | |url1=http://www.youtube.com/watch?v=QZlZAtIxtCo | ||
| + | }} | ||
| + | ---- | ||
| + | '''Raíces exactas:''' | ||
| + | |||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 212: | Línea 279: | ||
| :a) <math>\sqrt[4]{16}</math> | :a) <math>\sqrt[4]{16}</math> | ||
| :b) <math>\sqrt[5]{-243}</math> | :b) <math>\sqrt[5]{-243}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=9rj5h_rDlNY | + | |url1=http://www.youtube.com/watch?v=9rj5h_rDlNY |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 220: | Línea 287: | ||
| :a) <math>\sqrt[6]{64}</math> | :a) <math>\sqrt[6]{64}</math> | ||
| :b) <math>\sqrt[3]{-216}</math> | :b) <math>\sqrt[3]{-216}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=3sR7VxclkIE | + | |url1=http://www.youtube.com/watch?v=3sR7VxclkIE |
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 228: | Línea 295: | ||
| :a) <math>\sqrt{144}</math> | :a) <math>\sqrt{144}</math> | ||
| :b) <math>\sqrt{2304}</math> | :b) <math>\sqrt{2304}</math> | ||
| - | |url1=https://www.youtube.com/watch?v=NBDA-T0DA6w#t=40s | + | |url1=http://www.youtube.com/watch?v=NBDA-T0DA6w#t=40s |
| }} | }} | ||
| }} | }} | ||
Revisión actual
Tabla de contenidos |
Raíz n-ésima de un número
La raíz n-ésima 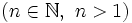 de un número
de un número  es otro número
es otro número  tal que
tal que 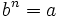 y que escribimos simbólicamente
y que escribimos simbólicamente ![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png) .
.
![\sqrt[n]{a}=b \iff b^n =a](/wikipedia/images/math/f/f/7/ff79017c635440f207b67b250c3660fb.png)
El número  se llama radicando, el número
se llama radicando, el número  índice y
índice y  la raíz.
la raíz.
Si el índice es 2 las llamaremos raíces cuadradas; si el índice es 3, raíces cúbicas; si es 5, 6, ..., raíces cuartas, quintas, ....
Propiedades de las raíces
Propiedades
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) ;
; ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
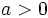 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
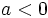 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 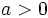 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
- Si el índice
 es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
Tutorial que explica la definición de raíz (radical) realizando el cálculo de alguna raíces exactas de números racionales (enteros y decimales).
Raíz n-ésmina de un número. Ejemplos sencillos.
Raíz n-ésmina de un número. Ejemplos más complejos.
Raíz n-ésmina de un número. Ejemplos sencillos.
- Raíces de un número entero.
- Raíces cuadradas y cúbicas.
- Partes de una raíz.
- Raíces de números positivo, negativos y del cero.
- Raíz exacta y raíz entera.
- Calculo manual de raíces cuadradas.
- Los radicales.
- Extracción de factores de un radical.
1) Completa:
- 1a)
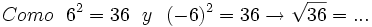
- 1b)
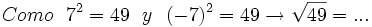
- 1c)
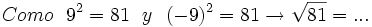
- 1d)
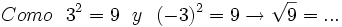
2) Completa:
- 2a)
![Como \ \ 6^3=216 \rightarrow \sqrt[3]{216}= ...](/wikipedia/images/math/3/c/3/3c378630d2615778e963ac624db86d87.png)
- 2b)
![Como \ \ (-6)^3=-216 \rightarrow \sqrt[3]{-216}= ...](/wikipedia/images/math/6/5/8/6587736293705d54e8f32954028d084c.png)
- 2c)
![Como \ \ 5^3=125 \rightarrow \sqrt[3]{125}= ...](/wikipedia/images/math/b/d/b/bdb68c764c3249b6a9780aa720742319.png)
- 2d)
![Como \ \ (-5)^3=-125 \rightarrow \sqrt[3]{-125}= ...](/wikipedia/images/math/e/7/0/e705216d0789f62aef7ec241081fabeb.png)
- 2e)
![Como \ \ 7^3=343 \rightarrow \sqrt[3]{343}= ...](/wikipedia/images/math/5/f/2/5f298eabe3ed377592f625e71f6488c0.png)
- 2f)
![Como \ \ (-7)^3=-343 \rightarrow \sqrt[3]{-343}= ...](/wikipedia/images/math/c/e/5/ce577674faca3babb2d3dfaac0413e21.png)
3) Completa:
- 3a)
![Como \ \ 6^4=216 \ \ y \ \ (-6)^4 =216 \rightarrow \sqrt[4]{216}= ...](/wikipedia/images/math/c/b/4/cb4b33e4c8e211ead755140a2c66bba9.png)
- 3b)
![Como \ \ 2^5=32 \ \ y \ \ (-2)^5 =32 \rightarrow \sqrt[5]{32}= ... \ \ y \ \ \sqrt[5]{-32}= ...](/wikipedia/images/math/c/c/c/ccc2a79c409e95a6ea8eb4d3dd464bae.png)
- 3c)
![Como \ \ 3^6=729 \ \ y \ \ (-3)^6 =729 \rightarrow \sqrt[6]{729}= ...](/wikipedia/images/math/b/5/5/b554d8cc9395627f020eb1f365124e4e.png)
- 3d)
![Como \ \ 2^7=128 \ \ y \ \ (-2)^7 =-128 \rightarrow \sqrt[7]{128}= ... \ \ y \ \ \sqrt[7]{-128}= ...](/wikipedia/images/math/a/d/6/ad64ef0e208078f3159cae14f80cd300.png)
- 3e)
![Como \ \ 3^8=6561 \ \ y \ \ (-3)^8 =6561 \rightarrow \sqrt[8]{6561}= ...](/wikipedia/images/math/7/b/a/7ba166f1a52a30e3ea2be20046fc6f29.png)
- 3f)
![Como \ \ 2^9=512 \ \ y \ \ (-2)^9 =-512 \rightarrow \sqrt[9]{512}= ... \ \ y \ \ \sqrt[9]{-512}= ...](/wikipedia/images/math/3/a/9/3a962574019bdc46ed38d924b83f207c.png)
- 3g)
![Como \ \ 2^{10}=1024 \ \ y \ \ (-2)^{10} =1024 \rightarrow \sqrt[10]{1024}= ...](/wikipedia/images/math/7/e/d/7edae10fccfe7b465c672d8c9c045b91.png)
4) Contesta:
- 4a) ¿Hay algún número que elevado al cuadrado dé -25? ¿Existe
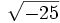 ?
?
- 4b) ¿Hay algún número que elevado al cuadrado dé -36? ¿Existe
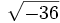 ?
?
- 4c) ¿hay algún número que elevado al cuadrado dé un número negativo?
- 4d) ¿Hay algún número que elevado al cubo dé -27? ¿Existe
![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png) ?
?
- 4e) ¿Hay algún número que elevado al cubo dé -64? ¿Existe
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png) ?
?
- 4f) ¿hay algún número que elevado al cubo dé un número negativo?
- 4g) ¿Hay algún número que elevado a la cuarta dé -81? ¿Existe
![\sqrt[4]{-81}\;](/wikipedia/images/math/9/3/8/9380cfbe25a5f6b1f53b0e98557d5cb3.png) ?
?
- 4h) ¿Hay algún número que elevado a la quinta dé -243? ¿Existe
![\sqrt[5]{-243}\;](/wikipedia/images/math/0/0/d/00d129c231e444389e6e90b5a1a8e808.png) ?
?
- 4i) ¿De qué depende que exista una raíz de radicando negativo?
5) Calcula:
- 5a)
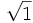 ;
; 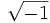
- 5b)
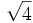 ;
; 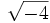
- 5c)
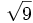 ;
; 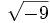
- 5d)
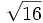 ;
; 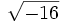
- 5e)
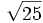 ;
; 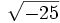
- 5f)
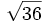 ;
; 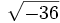
- 5g)
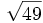 ;
; 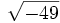
- 5h)
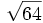 ;
; 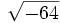
- 5i)
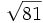 ;
; 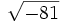
- 5j)
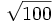 ;
; 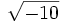
6) Calcula:
- 6a)
![\sqrt[3]{1}\;](/wikipedia/images/math/a/9/e/a9ed184fd0349444d061cc1d272e67c6.png) ;
; ![\sqrt[3]{-1}\;](/wikipedia/images/math/9/1/7/917ae3af6a2d50278779cc91cbbdea73.png)
- 6b)
![\sqrt[3]{8}\;](/wikipedia/images/math/1/3/2/132c2f74c8498afa99586eeab29a92a8.png) ;
; ![\sqrt[3]{-8}\;](/wikipedia/images/math/2/2/3/2232a48fe703bd572c3668d1f57c0066.png)
- 6c)
![\sqrt[3]{27}\;](/wikipedia/images/math/f/f/d/ffdb842d7cefcf30ac4e11b74ccdc8f3.png) ;
; ![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png)
- 6d)
![\sqrt[3]{64}\;](/wikipedia/images/math/4/b/d/4bd0c615f84c6543e9f004c6bcfce737.png) ;
; ![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 6e)
![\sqrt[3]{125}\;](/wikipedia/images/math/9/b/0/9b0b656102d06b662a6c1cfa6f46ee4c.png) ;
; ![\sqrt[3]{-125}\;](/wikipedia/images/math/b/d/6/bd68acb8f905cf5984575d47adbbe028.png)
6) Calcula:
- 7a)
![\sqrt[4]{1}\;](/wikipedia/images/math/4/2/3/42348ffb6e4d069c36b7529b4c3d61c7.png) ;
; ![\sqrt[4]{-1}\;](/wikipedia/images/math/3/0/4/3041c7b2e1985e0ce2b4e12419b1adfd.png)
- 7b)
![\sqrt[5]{32}\;](/wikipedia/images/math/5/a/4/5a4316aef4d84ea09023226c0b455ef1.png) ;
; ![\sqrt[5]{-32}\;](/wikipedia/images/math/e/4/b/e4b2e7ef8b833cd852ca9c1bedfade9b.png)
- 7c)
![\sqrt[6]{729}\;](/wikipedia/images/math/6/4/5/645cad2d63e42973a6e2a66d954d5272.png) ;
; ![\sqrt[6]{-729}\;](/wikipedia/images/math/c/8/9/c89f55205c50d79be31feca9e8e7fe21.png)
- 7d)
![\sqrt[7]{128}\;](/wikipedia/images/math/e/4/e/e4e24abf54c49df327ec72213ca1b2bd.png) ;
; ![\sqrt[7]{-128}\;](/wikipedia/images/math/5/7/f/57ff532d80dc61569bbab4448a648df4.png)
8) Indica, en cada caso, la raíz, el índice y el radicando:
- 8a)
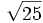
- 8b)
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 8c)
![\sqrt[4]{81}\;](/wikipedia/images/math/0/4/d/04d103e445158aa43cb56526c68b98c2.png)
9) Completa:
- 9a)
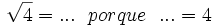
- 9b)
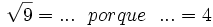
- 9c)
![\sqrt[3]{-8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/b/b/c/bbc65bbad66511345d7cb3ac4f7a001c.png)
- 9d)
![\sqrt[3]{8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/3/e/c/3ec4111d51daf4478bc80d3d1bd1ef0a.png)
- 9e)
![\sqrt[4]{16}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/2/0/8/208788fa3a4920a05007fa9edad8dbc6.png)
- 9f)
![\sqrt[5]{32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/f/5/5/f552d101987249877deb51a2875a57db.png)
- 9g)
![\sqrt[5]{-32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/a/b/9/ab988d19836d333dfc399b9f3fefee8c.png)
- 9f)
![\sqrt[6]{1}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/7/0/6/70646a208681230895b71a7e18b7317b.png)
10) Calcula las raíces enteras por exceso y por defecto:
- 10a)
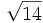 ;
; ![\sqrt[3]{14}\;](/wikipedia/images/math/4/d/9/4d90b08a8a7ba14e1c60f25be0fb24ef.png)
- 10b)
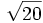 ;
; ![\sqrt[3]{20}\;](/wikipedia/images/math/f/a/a/faaf025a7b9f3b036eb836c60d8e4e34.png)
- 10c)
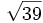 ;
; ![\sqrt[3]{39}\;](/wikipedia/images/math/c/9/f/c9f16a3fa799c3b21b4f313600db621c.png)
11) Calcula a mano las siguientes raíces:
- 11a)
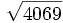
- 11b)

11) Calcula a mano las siguientes raíces:
- 11c)
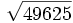
- 11d)
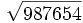
- 11e)
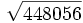
- 11f)
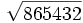
Actividades para que aprendas a calcular la raíz n-ésima de un número entero.
La raíz como potencia de exponente fraccionario
Proposición: La raíz como potencia de exponente fraccionario
Toda raíz se puede expresar como una potencia de la siguiente forma:
|
|
Basta con ver que se cumple la condición de la definición de raíz:
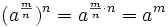
Ejemplo: La raíz como potencia de exponente fraccionario
Escribe las siguientes raíces como potencias de exponente fraccionario y calcula su valor:
a) 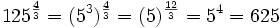
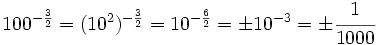 (por ser el índice par tiene dos soluciones de signos opuestos)
(por ser el índice par tiene dos soluciones de signos opuestos)Potencia de exponente fraccionario. Ejemplos.
Potencia de exponente fraccionario. Ejemplos.
Potencia de exponente fraccionario. Ejemplos.
Expresa como potencia de exponente fraccionario:
- a)
![\sqrt[5]{b^9}](/wikipedia/images/math/c/b/9/cb9fc88c51f111bf29a3da084ddafdb4.png)
- b)
![\sqrt[6]{g^5}](/wikipedia/images/math/b/8/2/b82a93b7500035423187e5a378387cc5.png)
- c)
![\cfrac{1}{\sqrt[7]{x}}](/wikipedia/images/math/7/1/1/711fca9584b1002a983e18467e624273.png)
Averigua el valor de a:
Averigua el valor de k:
Simplifica:
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Ejercicios de autoevaluación sobre potencias de exponente fraccionario.
Propiedades de las potencias de exponente fraccionario
Las potencias con exponente fraccionario tienen las mismas propiedades que con exponente natural o entero.
Calcula:
- a)
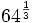
- b)
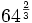
- c)
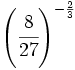
Calcula:
- a)
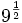
- b)
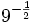
- c)
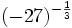
Calcula:
- a)
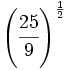
- b)
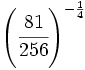
Calcula:
Simplifica:
Actividades para que aprendas a operar con raíces expresadas en forma de potencias de exponente fraccionario y a utilizar sus propiedades.
Simplifica expresiones radicales
Raíces exactas e inexactas
Se llaman raíces exactas de un número a aquellas que dan como resultado un número racional. En caso contrario diremos que son inexactas y el resultado será un número irracional.
Raíces exactas e inexactas
Para que una raíz sea exacta, al descomponer el radicando en factores primos, los exponentes de éstos deben ser todos divisibles por el índice de la raíz.
Ejemplo: Raíces exactas e inexactas
Calcula las siguientes raíces cuando sean exactas:
a) Descomponemos 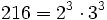 .
.
Como las potencias son divisibles por 3, la raíz es exacta. Para obtenerla, la regla práctica consiste en dividir cada exponente entre el índice. A continuación se explica el porqué de forma detallada:
![\sqrt[3]{216}=\sqrt[3]{2^3 \cdot 3^3}=(2^3 \cdot 3^3)^{\frac{1}{3}}=2^{\frac{3}{3}} \cdot 3^{\frac{3}{3}}=2^1 \cdot 3^1=6](/wikipedia/images/math/9/0/f/90ff62c218ce74b95403e00069fa46ec.png)
Luego ![\sqrt[3]{216}](/wikipedia/images/math/2/a/6/2a60cb9da80e1f9abad0623c37ccfb67.png) es racional.
es racional.
b) Descomponemos 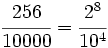 .
.
Como las potencias son divisibles por 4, la raíz es exacta. Para obtenerla, dividimos cada exponente entre el índice:
![\sqrt[4]{0.0256}=\sqrt[4]{\cfrac{256}{10000}}=\sqrt[4]{\cfrac {2^8}{10^4}}=\cfrac {2^{\frac{8}{4}}}{10^{\frac{4}{4}}}=\pm \cfrac{2^2}{10^1}=\pm \cfrac{4}{10}=\pm 0'4](/wikipedia/images/math/2/1/1/2111a7f15ed884cde82acb4bee2152c1.png)
Luego ![\sqrt[4]{0.0256}](/wikipedia/images/math/f/e/0/fe057f07425971a1f2db4869683fe6bd.png) es racional.
es racional.
c) Descomponemos 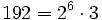 .
.
El exponente de 3 es 1, que no es divisible por 3. Por tanto, la raíz no es exacta.
Luego![\sqrt[3]{192}](/wikipedia/images/math/b/d/f/bdfe841e1073096ee42922125fc7e19d.png) es irracional.
es irracional.Tutorial que explica las raíces exactas e inexactas y pone ejemplos de ambas.
Raíces exactas:
Calcula:
- a)
![\sqrt[4]{16}](/wikipedia/images/math/0/8/5/08539911f08513b980a050e5bd399ead.png)
- b)
![\sqrt[5]{-243}](/wikipedia/images/math/6/3/5/635e97dd723ead900066d5383852216f.png)
Calcula:
- a)
![\sqrt[6]{64}](/wikipedia/images/math/4/7/2/472e429662dd1bbb544e8af33cf8e11b.png)
- b)
![\sqrt[3]{-216}](/wikipedia/images/math/1/9/0/1900c7889aa4b60b66f43b9dc348d52c.png)
Calcula:
- a)
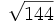
- b)
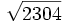
Raíces de fracciones
Cómo se calculan las raíces de fracciones. Ejemplos.
Cómo se suman y restan las raíces de fracciones. Ejemplos.
Cómo se multiplican raíces de fracciones. Ejemplos.
Cómo se dividen raíces de fracciones. Ejemplos.
Cómo se calculan las potencias de raíces de fracciones. Ejemplos.
Cómo se calculan las raíces de raíces de fracciones. Ejemplos.
Suma y resta de raíces de fracciones:
- 1)
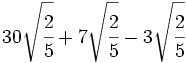
- 2)
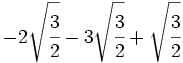
- 3)
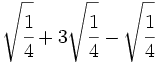
- 4)
![-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/f/5/5/f55a7abe041410d0d772b3f5f9249888.png)
- 5)
![-8\sqrt[3]{\cfrac{-3}{5}}+\cfrac{3}{2}\sqrt[3]{\cfrac{-3}{5}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-3}{5}}](/wikipedia/images/math/c/7/e/c7e1346a8d6ef7ddeb7f7c7972383303.png)
Suma y resta de raíces de fracciones:
- 6)
![\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+2\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/e/7/4/e74f2414908471712a21bcd2c0727973.png)
- 7)
![\sqrt[8]{\cfrac{9}{4}}+12\sqrt[8]{\cfrac{9}{4}}-\cfrac{1}{4}\sqrt[8]{\cfrac{9}{4}}](/wikipedia/images/math/7/9/5/7956651986adce493726a51fce226382.png)
- 8)
![\cfrac{-1}{3}\sqrt[11]{\cfrac{-3}{7}}+\cfrac{1}{9}\sqrt[11]{\cfrac{-3}{7}}-\cfrac{2}{3}\sqrt[11]{\cfrac{-3}{7}}](/wikipedia/images/math/f/c/e/fceb6863061e8ca281259ac86890e169.png)
- 9)
![-\sqrt[5]{\cfrac{5}{3}}-\cfrac{5}{2}\sqrt[5]{\cfrac{5}{3}}-\cfrac{1}{4}\sqrt[5]{\cfrac{5}{3}}](/wikipedia/images/math/9/2/2/92245797897977068795b35dc3cbcfc7.png)
Multiplicaciones de raíces de fracciones:
- 10)
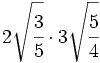
- 11)
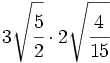
- 12)
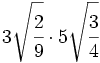
- 13)
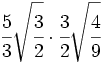
Multiplicaciones de raíces de fracciones:
- 14)
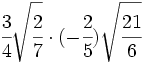
- 15)
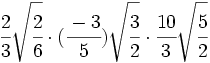
- 16)
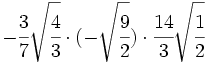
Multiplicaciones de raíces de fracciones:
- 17)
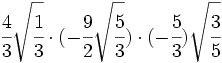
- 18)
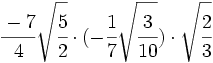
- 19)
![2\sqrt[3]{\cfrac{2}{5}} \cdot 3\sqrt[3]{\cfrac{4}{25}}](/wikipedia/images/math/f/8/1/f81614b373a70320fa5bbee491ded79d.png)
- 20)
![\sqrt[3]{\cfrac{9}{2}} \cdot \cfrac{5}{6}\sqrt[3]{\cfrac{2}{125}}](/wikipedia/images/math/f/d/b/fdbcdfd572102f2971190e92ad2b9ca8.png)
Multiplicaciones de raíces de fracciones:
- 21)
![\cfrac{-2}{5}\sqrt[3]{\cfrac{-1}{3}} \cdot 5\sqrt[3]{\cfrac{-1}{9}}](/wikipedia/images/math/e/1/d/e1dc683585b12c3e8f8b0336e6cd3dce.png)
- 22)
![2\sqrt[3]{\cfrac{7}{3}} \cdot \cfrac{1}{4}\sqrt[3]{\cfrac{9}{14}}](/wikipedia/images/math/4/e/5/4e5561c3d3d0f4cadb26ebea76193f5e.png)
- 23)
![8\sqrt[3]{\cfrac{3}{7}} \cdot \sqrt[3]{\cfrac{-7}{9}} \cdot \sqrt[3]{\cfrac{-7}{2}}](/wikipedia/images/math/9/9/9/99904e001c4c05d9a33cc7f20320c6eb.png)
Multiplicaciones de raíces de fracciones:
- 24)
![3\sqrt[3]{\cfrac{9}{4}} \cdot \left( -\cfrac{1}{2}\sqrt[3]{\cfrac{3}{2}} \right) \cdot \cfrac{2}{5}\sqrt[3]{125}](/wikipedia/images/math/d/3/c/d3cb69b0f72a7fed15f71aa8513dfbb6.png)
- 25)
![\cfrac{4}{3}\sqrt[4]{\cfrac{3}{7}} \cdot 3\sqrt[4]{\cfrac{16}{3}}](/wikipedia/images/math/b/d/5/bd5b5b76b496c2f6825e62489c158052.png)
- 26)
![\cfrac{1}{3}\sqrt[8]{\cfrac{1}{4}} \cdot \left( -\cfrac{9}{2}\sqrt[8]{\cfrac{2}{3}} \right) \cdot 4\sqrt[8]{\cfrac{3}{5}}](/wikipedia/images/math/7/4/4/74408c6f3e91a102054dcf8b4a208595.png)
División de raíces de fracciones:
- 27)
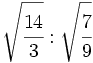
- 28)
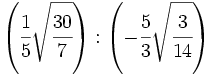
- 29)
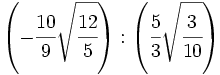
- 30)
![\left( -\cfrac{2}{3}\sqrt[3]{\cfrac{14}{5}} \right): \left( \cfrac{14}{12}\sqrt[3]{\cfrac{7}{10}} \right)](/wikipedia/images/math/a/9/1/a913d1108fd67aec4f52e62b81efa9e8.png)
División de raíces de fracciones:
- 31)
![\left( \cfrac{9}{2}\sqrt[3]{\cfrac{14}{9}} \right) : \left( \sqrt[3]{\cfrac{-7}{3}} \right)](/wikipedia/images/math/8/9/e/89e41ac40d647d9d9d10fd9f080b8f9c.png)
- 32)
![\left( \cfrac{12}{5}\sqrt[3]{\cfrac{18}{3}} \right): \left( -\cfrac{6}{5}\sqrt[3]{\cfrac{-9}{2}} \right)](/wikipedia/images/math/7/8/b/78b4e0f5d87c167f3b7d0e410f45c6ec.png)
División de raíces de fracciones:
- 33)
![\left( -\cfrac{10}{3}\sqrt[4]{\cfrac{15}{49}} \right) : \left( \cfrac{5}{27}\sqrt[4]{\cfrac{49}{125}} \right)](/wikipedia/images/math/a/6/4/a64ae58b74db2719880d0c4bceb986c7.png)
- 34)
![\left( -\cfrac{10}{4}\sqrt[5]{\cfrac{15}{7}} \right): \left( \cfrac{5}{6}\sqrt[5]{\cfrac{5}{14}} \right)](/wikipedia/images/math/9/4/7/9479dbe129a893330d386ef04c8dddcb.png)
- 35)
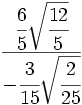
División de raíces de fracciones:
- 36)
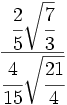
- 37)
![\cfrac{-\cfrac{10}{7}\sqrt[3]{\cfrac{15}{4}}}{5\sqrt[3]{\cfrac{8}{9}}}](/wikipedia/images/math/3/f/7/3f7ec32f3c77881d616b8760375d4d6f.png)
- 38)
![\cfrac{-\cfrac{10}{6}\sqrt[3]{\cfrac{15}{4}}}{\cfrac{5}{3}\sqrt[3]{\cfrac{2}{25}}}](/wikipedia/images/math/2/f/5/2f578dac94a33d0ddc501f0c60f4fffb.png)
Potencias de raíces de fracciones:
- 39)
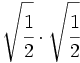
- 40)
![\sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}}](/wikipedia/images/math/6/3/9/63995d3707778bdb86de378c75aca586.png)
- 41)
![\sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}}](/wikipedia/images/math/6/3/3/633c62efe0db98851d8196c7d058cbe0.png)
- 42)
![\sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}}](/wikipedia/images/math/9/0/e/90e63a779d9f738b1332ad73f20d0c44.png)
- 43)
![\sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}}](/wikipedia/images/math/9/f/0/9f0f9afc0dba273231a5b490e098027d.png)
Convierte en potencias de exponente fraccionario:
- 44)
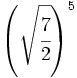 ; 45)
; 45) 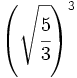 ; 46)
; 46) 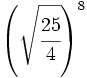
- 47)
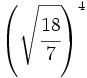 ; 48)
; 48) 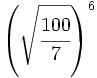 ; 49)
; 49) ![\left( \sqrt[3]{\cfrac{7}{3}} \right)^6](/wikipedia/images/math/7/6/3/763844586d27849f01b0f220f197d4d0.png)
- 50)
![\left( \sqrt[3]{\cfrac{5}{2}} \right)^9](/wikipedia/images/math/5/b/7/5b7af58a06ea229f4169c8f038eeb6a0.png) ; 51)
; 51) ![\left( \sqrt[4]{\cfrac{7}{4}} \right)^8](/wikipedia/images/math/0/e/0/0e0e0fafb99b320da94e2293f4f14701.png) ; 52)
; 52) ![\left( \sqrt[6]{\cfrac{21}{5}} \right)^{12}](/wikipedia/images/math/a/0/7/a07d93d0c3029249c9933a99a2eb2728.png)
- 53)
![\left( \sqrt[21]{\cfrac{12}{5}} \right)^{14}](/wikipedia/images/math/5/5/3/55309d54139afb8fbea7172261e4f109.png)
Convierte la potencia en raíz:
- 54)
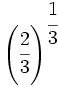 ; 55)
; 55) 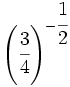 ; 56)
; 56) 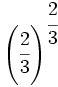
- 57)
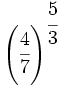 ; 58)
; 58) 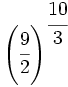 ; 59)
; 59) 
Raíces de una raíz de una fracción:
- 60)
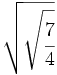 ; 61)
; 61) 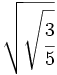 ; 62)
; 62) 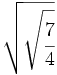
- 63)
![\sqrt[3]{\sqrt{\cfrac{2}{5}}}](/wikipedia/images/math/f/e/9/fe9d5ed19933ef100bc8b0f67559fa52.png) ; 64)
; 64) ![\sqrt[3]{\sqrt[3]{\cfrac{25}{4}}}](/wikipedia/images/math/7/b/3/7b3a4b58a2b91246bf250ff1abd743b3.png) ; 65)
; 65) ![\sqrt{\sqrt[3]{64}}](/wikipedia/images/math/0/e/d/0eddc7f2593e00fd623113cf77aff52f.png)
- 66)
![\sqrt[4]{\sqrt[3]{\cfrac{2}{7}}}](/wikipedia/images/math/e/b/e/ebedfae4b0471be70ea604bbe26e5e19.png) ; 67)
; 67) ![\sqrt[3]{\sqrt{\cfrac{12}{5}}}](/wikipedia/images/math/2/f/5/2f5c1b5dfc0e771272ee1b0c8e2ac6db.png)
Calculadora
Raíz cuadrada
|
Calculadora: Raíz cuadrada |
Raíz cúbica
|
Calculadora: Raíz cúbica |
Otras raíces
|
Calculadora: Otras raíces |
![\sqrt[5]{32}=2\;](/wikipedia/images/math/e/f/a/efae07f29bbbaaef03acb5b46afffb59.png) porque
porque 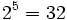 .
.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 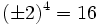 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 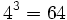 .
.
![\sqrt[3]{-8}=-2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png) porque
porque 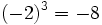 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).
![\sqrt[n]{a^m}=a^\frac{m}{n}](/wikipedia/images/math/3/b/0/3b0234682d54453ceee722e89c782c2e.png)
![a)\ \sqrt[3] {125^4} \quad b)\ \sqrt {100^{-3}}](/wikipedia/images/math/5/9/e/59ebdba87736732560d47ebf9c21a75e.png)
![3^a=\sqrt[5]{3^2}](/wikipedia/images/math/6/d/8/6d842078dcc499bd8f7362de399b3095.png)
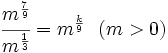
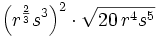
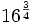
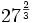
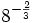
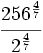
![6^{\frac{1}{2}} \cdot \left(\sqrt[5]{6}\right)^3](/wikipedia/images/math/6/5/e/65e6f10ec848c362c461db20665256a8.png)
![a) \sqrt[3]{216} \quad b) \sqrt[4]{0.0256}\quad c) \sqrt[3]{192}](/wikipedia/images/math/d/f/7/df7f4bb983c565de5f6c5ab3ff89efdd.png)
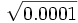
![\sqrt[3] {-512}](/wikipedia/images/math/d/5/0/d5007990ae7e9a5dddf6e4eff90d9a71.png)
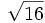
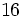
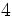
![\sqrt [3] {8}](/wikipedia/images/math/f/5/2/f5234f8dd97fefc954cf62fa258a3b72.png)
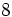

![\sqrt [4]{81}](/wikipedia/images/math/e/c/6/ec6e7957bf989cbaf4c80a2e4c59755c.png)