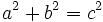Plantilla:Teorema de Pitágoras
De Wikipedia
| Revisión de 09:44 21 abr 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Teorema|titulo=Teorema de Pitágoras|enunciado= | {{Teorema|titulo=Teorema de Pitágoras|enunciado= | ||
| - | {{Tabla75|celda1=En un [[Triángulos#Triángulos rectángulos | triángulo rectángulo]] la hipotenusa al cuadrado es igual al cuadrado de la suma de los catetos | + | {{Tabla75|celda1=En un [[Triángulos#Triángulos rectángulos | triángulo rectángulo]] la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos: |
| <br> | <br> | ||
| {{Caja|contenido=<math>a^2+b^2=c^2\;\!</math>}} | {{Caja|contenido=<math>a^2+b^2=c^2\;\!</math>}} | ||
| <br> | <br> | ||
| - | donde <math>a\;\!</math> y <math>b\;\!</math> son los catetos y <math>c\;\!</math> la hipotenusa. | + | donde {{sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} y {{sube|porcentaje=+20%|contenido=<math>b\;\!</math>}} son los catetos y {{sube|porcentaje=+10%|contenido=<math>c\;\!</math>}} la hipotenusa. |
| <br> | <br> | ||
| Línea 14: | Línea 14: | ||
| <table align="center"> | <table align="center"> | ||
| <tr> | <tr> | ||
| - | <td>Fíjate en la figuar de la derecha y observa como el cuadrado grande, de lado <math>a+b</math>, puede descomponerse en un cuadrado de lado <math>c</math> y 4 triángulos rectángulos, como el de partida, de catetos <math>a</math> y <math>b</math> e hipotenusa <math>c</math>. | + | <td>Fíjate en la figura de la derecha y observa como el cuadrado grande, de lado <math>a+b</math>, puede descomponerse en un cuadrado de lado <math>c</math> y 4 triángulos rectángulos, como el de partida, de catetos <math>a</math> y <math>b</math> e hipotenusa <math>c</math>. |
| La superficie del cuadrado grande de lado <math>a+b</math> es: | La superficie del cuadrado grande de lado <math>a+b</math> es: | ||
| <center><math>(a+b)^2=a^2+b^2+2ab\;\!</math></center> | <center><math>(a+b)^2=a^2+b^2+2ab\;\!</math></center> | ||
| Línea 28: | Línea 28: | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| - | ----[http://maralboran.ath.cx/web_ma/descartes/3_eso/Demostraciones_graficas_teorema_pitagoras/Demostraciones_1.htm#INTRODUCCIÓN Otras demostraciones gráficas] | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Teorema de Pitágoras''|cuerpo= | + | {{Videotutoriales|titulo=Teorema de Pitágoras|enunciado= |
| - | {{ai_cuerpo | + | '''Teorema de Pitágoras:''' |
| - | |enunciado='''Actividad 1:''' Dado el triángulo de lados b=3, c=4 y a=5, comprueba el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo. | + | {{Video_enlace_sensei |
| - | |actividad= | + | |titulo1=Tutorial 1 |
| - | <center><iframe> | + | |duracion=7'24" |
| - | url=http://maralboran.org/web_ma/descartes/Geometria/pitagoras_pgs/Teorema_de_Pitagoras_2.html | + | |sinopsis=Teorema de Pitágoras. Ejemplos y ejercicios. |
| - | width=500 | + | |url1=https://youtu.be/D4IvZQEenT8 |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/pitagoras_pgs/Teorema_de_Pitagoras_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| }} | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=10'54" | ||
| + | |sinopsis=Teorema de Pitágoras. Ejemplos y ejercicios. | ||
| + | |url1=https://youtu.be/Pcnpckjwkig?list=PLwCiNw1sXMSCaukmrbPRm2SQuhas4kWS_ | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_masterd |
| - | {{Video2 | + | |titulo1=Tutorial 3 |
| - | |titulo1=Pitágoras: mucho más que un teorema | + | |duracion=2'17" |
| - | |duracion=25´ | + | |sinopsis=Teorema de Pitágoras. Ejemplos. |
| - | |url1=http://maralboran.org/web_ma/videos/pitagoras/pitagoras.htm | + | |url1=https://www.youtube.com/watch?v=J4QbmOqgVvg&index=3&list=PL22187EA37AFFD9C3 |
| - | |titulo2=Acceso por red TIC | + | |
| - | |url2=http://c0/helvia/aula/archivos/repositorio//0/97/html/index.htm | + | |
| - | |sinopsis=Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia. | + | |
| }} | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Tutorial 4 | ||
| + | |duracion=2'15" | ||
| + | |url1=https://www.youtube.com/watch?v=kbU38TEpptI | ||
| + | |sinopsis=Teorema de Pitágoras y recíproco. Ejemplo. | ||
| + | }} | ||
| + | ---- | ||
| + | '''Demostraciones:''' | ||
| + | |||
| + | {{Video_enlace_unpuntocircular | ||
| + | |titulo1=Demostración 1 | ||
| + | |duracion=4´29" | ||
| + | |url1=https://www.youtube.com/watch?v=7CQ9aE8FgoQ | ||
| + | |sinopsis=Demostración del teorema de Pitágoras mediante una construcción geométrica, con ejemplos previos de casos particulares. | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Demostración 2 | ||
| + | |duracion=5'00" | ||
| + | |url1=https://www.youtube.com/watch?v=nDODDfzYtUQ | ||
| + | |sinopsis=La misma demostración del teorema de Pitágoras mediante una construcción geométrica, sin ejemplos previos. | ||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| - | {{Web2 | + | {{Videotutoriales|titulo=Demostración 3|enunciado= |
| - | |titulo=Teorema de Pitágoras | + | Otra demostración basada en el teorema de la altura y el teorema del cateto. |
| - | |descripcion=Web de D. Manuel Sada Allo. | + | |
| - | |pagina= | + | |
| - | <center><iframe> | + | |
| - | url=http://recursos.pnte.cfnavarra.es/~msadaall/geogebra/pitagoras.htm | + | |
| - | width=100% | + | |
| - | height=700 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://recursos.pnte.cfnavarra.es/~msadaall/geogebra/pitagoras.htm'''Click''' aquí si no se ve bien la escena]</center> | + | |
| + | Consta de tres partes: | ||
| + | |||
| + | {{Video_enlace_abel | ||
| + | |titulo1=1. Teorema de la altura | ||
| + | |duracion=13´57" | ||
| + | |url1=https://www.youtube.com/watch?v=AnFJcUea6tI | ||
| + | |sinopsis=Demostración del teorema de de la altura. | ||
| }} | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=2. Teorema del cateto | ||
| + | |duracion=16´16" | ||
| + | |url1=https://www.youtube.com/watch?v=n2jdLT5kzZs&t=420s | ||
| + | |sinopsis=Demostración del teorema del cateto. | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=3. Teorema de Pitágoras | ||
| + | |duracion=15´24" | ||
| + | |url1=https://www.youtube.com/watch?v=7mV-h918NCA | ||
| + | |sinopsis=Demostración del teorema de Pitágoras. | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ---- | ||
| + | '''Otros videos:''' | ||
| + | |||
| + | {{Video_enlace | ||
| + | |titulo1=Pitágoras y su teorema | ||
| + | |duracion=9'56" | ||
| + | |sinopsis=Pitágoras. El teorema de Pitágoras. Demostraciones. | ||
| + | |url1=https://www.youtube.com/watch?v=5eZ8OQgbVqA | ||
| + | }} | ||
| + | {{Video: Pitágoras: mucho más que un teorema}} | ||
| + | }} | ||
| + | {{Actividades|titulo=Teorema de Pitágoras|enunciado= | ||
| + | {{AI_descartes | ||
| + | |titulo1=Demostraciones gráficas | ||
| + | |descripcion=Esta unidad didáctica presenta varias demostraciones del teorema de Pitágoras. | ||
| + | |url1=http://maralboran.org/web_ma/descartes/3_eso/Demostraciones_graficas_teorema_pitagoras/Demostraciones_1.htm#INTRODUCCIÓN | ||
| + | }} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás comprobar el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo. | ||
| + | |enlace=[http://www.geogebra.org/m/n7JkKzy5 Comprobación geométrica] | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
Revisión actual
Teorema de Pitágoras
| En un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos:
| 
|
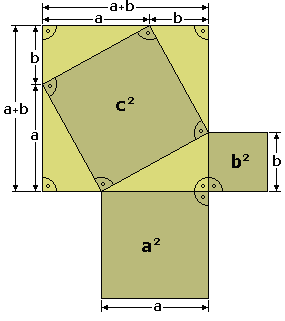
| Fíjate en la figura de la derecha y observa como el cuadrado grande, de lado a + b, puede descomponerse en un cuadrado de lado c y 4 triángulos rectángulos, como el de partida, de catetos a y b e hipotenusa c.
La superficie del cuadrado grande de lado a + b es: 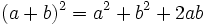 La superficie de los cuatro triángulos rectángulos es : 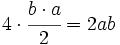 Restando el área del cuadrado grande de lado a + b menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado c: 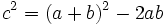 Desarrollando el cuadrado del binomio: 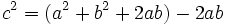 De donde obtenemos, simplificando:  |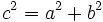
 |
Teorema de Pitágoras:
Tutorial 1 (7'24") Sinopsis:Teorema de Pitágoras. Ejemplos y ejercicios.
Tutorial 2 (10'54") Sinopsis:Teorema de Pitágoras. Ejemplos y ejercicios.
Tutorial 3 (2'17") Sinopsis:Teorema de Pitágoras. Ejemplos.
Tutorial 4 (2'15") Sinopsis:Teorema de Pitágoras y recíproco. Ejemplo.
Demostraciones:
Demostración 1 (4´29") Sinopsis: Demostración del teorema de Pitágoras mediante una construcción geométrica, con ejemplos previos de casos particulares.
Demostración 2 (5'00") Sinopsis:La misma demostración del teorema de Pitágoras mediante una construcción geométrica, sin ejemplos previos.
Otra demostración basada en el teorema de la altura y el teorema del cateto.
Consta de tres partes:
1. Teorema de la altura (13´57") Sinopsis:Demostración del teorema de de la altura.
2. Teorema del cateto (16´16") Sinopsis:Demostración del teorema del cateto.
3. Teorema de Pitágoras (15´24") Sinopsis:Demostración del teorema de Pitágoras.
Otros videos:
Pitágoras y su teorema (9'56") Sinopsis:Pitágoras. El teorema de Pitágoras. Demostraciones.
Pitágoras: mucho más que un teorema (25´) Sinopsis:Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Demostraciones gráficas Descripción: Esta unidad didáctica presenta varias demostraciones del teorema de Pitágoras.
Comprobación geométrica Descripción: En esta escena podrás comprobar el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo.
