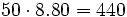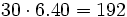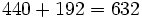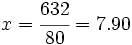Problemas clásicos (3ºESO Académicas)
De Wikipedia
| Revisión de 10:45 13 ago 2017 Coordinador (Discusión | contribuciones) (→Repartos proporcionales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Grifos) |
||
| Línea 9: | Línea 9: | ||
| (Pág. 47) | (Pág. 47) | ||
| ==Repartos proporcionales== | ==Repartos proporcionales== | ||
| - | {{Caja_Amarilla|texto=En los '''repartos proporcionales''' tenemos que repartir una cantidad en varias partes, de manera que cada parte sea proporcional a cada fracción en que se parte el total.}} | + | {{Repartos proporcionales}} |
| - | {{p}} | + | |
| - | {{Ejemplo | + | |
| - | |titulo=Ejercicio resuelto: ''Repartos proporcionales'' | + | |
| - | |enunciado={{p}} | + | |
| - | Tres grifos aportan 2 l/s, 5 l/s y 7l/s, respectivamente. Se abren los tres simultaneamente para llenar una balsa de 17080 l. Cuando la balsa está llena, ¿qué volumen de agua habrá manado de cada grifo? | + | |
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Los tres grifos aportan <math> 2+5+7=14 \ l/s</math>, de manera que: | + | |
| - | + | ||
| - | El primero aporta <math>\cfrac{2}{14}\;</math> del total <math>\rightarrow \cfrac{2}{14} \cdot 17080 = 2440 \ l</math> | + | |
| - | + | ||
| - | El segundo aporta <math>\cfrac{5}{14}\;</math> del total <math>\rightarrow \cfrac{5}{14} \cdot 17080 = 6100 \ l</math> | + | |
| - | + | ||
| - | El tercero aporta <math>\cfrac{7}{14}\;</math> del total <math>\rightarrow \cfrac{7}{14} \cdot 17080 = 8540 \ l</math> | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Videotutoriales|titulo=Reparto proporcional directo|enunciado= | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Problema 1 | + | |
| - | |duracion=17'03" | + | |
| - | |sinopsis=Tutorial que explica un problema concreto de proporcionalidad directa que es el de un reparto, viendo distintos métodos de resolución: por proporciones/porcentajes, reducción a la unidad, proporcionalidad y regla de tres: | + | |
| - | + | ||
| - | '''Problema:''' Tres amigos, Ana, Berta y Carlos, decidieron echar una quiniela de futbol poniendo cada uno de ellos, 6, 15 y 9 €, respectivamente. Después del fin de semana se enteraron que habían tenido 12 aciertos y que les había tocado un premio total de 1200 €. ¿Cuánto dinero le corresponderá a cada uno de ellos? | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=W_4X-n6gV1U&index=4&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa | + | |
| - | }} | + | |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Problemas 2 | + | |
| - | |duracion=6'50" | + | |
| - | |sinopsis=Reparto proporcional directo: | + | |
| - | + | ||
| - | #La comunidad de una urbanización encarga su pintado a tres empresas. La empresa A pinta 50 pisos, la B, 39, y la C, 51. El coste del pintado asciende a 70000€. ¿Cuánto ha cobrado cada empresa? | + | |
| - | + | ||
| - | #Tres amigos deciden formar una peña de apuestas deportivas. Pedro aporta 45 €, Laura 31 € y Agustín 44 €. En una apuesta ganan 55000 € y deciden repartirlo. ¿Cuánto le corresponde a cada uno? | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=v8KN44iNPls&list=PLWRbPOo5oaTfZHG7NVCJbQScXnnXSKvCw&index=6 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Problema 2 | + | |
| - | |duracion=3'43" | + | |
| - | |sinopsis= Reparto proporcional directo: | + | |
| - | + | ||
| - | Tres amigos compran lotería por valor de 20$. El primero pone 6$, el segundo 9$ y el tercero 5$. Si ganan un premiode 4000$, ¿cuánto le corresponde a cada uno? | + | |
| - | |url1=https://www.youtube.com/watch?v=NEk9UaH4NBQ | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Videotutoriales|titulo=Reparto proporcional inverso|enunciado= | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Problema 1 | + | |
| - | |duracion=9'15" | + | |
| - | |sinopsis=Tutorial que explica un problema concreto de reparto proporcional inverso. | + | |
| - | + | ||
| - | '''Problema:''' Tres amigos, Ana, Berta y Carlos, decidieron echar una carrera, en la cual tardaron 2, 3 y 4 minutos, respectivamente. Antes de la misma, acordaron repartirse 390 cromos de una colección en función del tiempo empleado en la carrera. ¿Cuántos cromos le corresponden a cada uno de ellos? | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=ZSyHq_NMm0U&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa&index=5 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Problema 2 | + | |
| - | |duracion=5'46" | + | |
| - | |sinopsis=Reparto proporcional inverso: | + | |
| - | + | ||
| - | Se va a repartir una gratificación por puntualidad consistente en 38$, entre 3 empleados de una oficina. Sabiendo que han tenido 2, 4 y 5 retrasos, respectivamente, ¿cuánto dinero recibe cada uno? | + | |
| - | |url1=https://www.youtube.com/watch?v=9Ig7x18ZbHw | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{AI_vitutor | + | |
| - | |titulo1=Autoevaluación: ''Repartos directamente proporcionales'' | + | |
| - | |descripcion=Problemas de autoevaluación sobre repartos directamente proporcionales. | + | |
| - | |url1=http://www.vitutor.com/di/p/a_6e.html | + | |
| - | }} | + | |
| - | {{AI_vitutor | + | |
| - | |titulo1=Autoevaluación: ''Repartos inversamente proporcionales'' | + | |
| - | |descripcion=Problemas de autoevaluación sobre repartos inversamente proporcionales. | + | |
| - | |url1=http://www.vitutor.com/di/p/a_10e.html | + | |
| - | }} | + | |
| - | {{Ejercicios_vitutor | + | |
| - | |descripcion=Problemas resueltos sobre repartos proporcionales. | + | |
| - | |url1=http://www.vitutor.com/di/p/ejercicios_reparto.html | + | |
| - | |titulo1=Problemas resueltos: ''Repartos proporcionales'' | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 155: | Línea 73: | ||
| {{problemas de mezclas}} | {{problemas de mezclas}} | ||
| }} | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 255: | Línea 174: | ||
| |sinopsis=Problemas de móviles. | |sinopsis=Problemas de móviles. | ||
| }} | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Problemas 9 | ||
| + | |duracion=14´58" | ||
| + | |url1=https://youtu.be/QkmbUmqt84Y?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | |sinopsis=Problemas de móviles. | ||
| }} | }} | ||
| + | |||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 269: | Línea 196: | ||
| ==Grifos== | ==Grifos== | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=5´07" | ||
| + | |sinopsis=Un grifo tarda 4h en llenar un recipiente y a otro le cuesta 12h. ¿Cuánto tardaremos si abrimos los dos grifos a la vez? | ||
| + | |url1=https://youtu.be/oz78JG2kpys?list=PLLfTN7MHLxConbepI-_1OEy-pjAxI8IvH | ||
| + | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=6´18" | ||
| + | |sinopsis=Tres grifos tardan 2h y 40min en llenar una piscina. Sabiendo que uno de ellos lo hace en solo 6h y el otro en 8h, ¿cuánto tardará el tercero? | ||
| + | |url1=https://youtu.be/uJlCMxOyGNA?list=PLLfTN7MHLxConbepI-_1OEy-pjAxI8IvH | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Problema 3 | ||
| + | |duracion=6'24" | ||
| + | |sinopsis=Problema de grifos. | ||
| + | |url1=https://youtu.be/bGq7FJ6YE6o?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Problema 4 | ||
| + | |duracion=8'19" | ||
| + | |sinopsis=Problemas de grifos. | ||
| + | |url1=https://youtu.be/CQlj8yCk6tA?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Problema 5 | ||
| + | |duracion=7'43" | ||
| + | |sinopsis=Problemas de grifos. | ||
| + | |url1=https://youtu.be/oV85hDE3Yxw?list=PLwCiNw1sXMSA5afCSBZn9Y9X9F732nicE | ||
| + | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Problema de grifos | + | |titulo1=Problema 6 |
| |duracion=12´08" | |duracion=12´08" | ||
| |sinopsis=Un caño llena un tanque en 4 horas y un desagüe lo vacía en 6 horas. ¿En cuánto tiempo se llenará el tanque si la llave del desagüe empieza a funcionar una hora después de abierto el caño? | |sinopsis=Un caño llena un tanque en 4 horas y un desagüe lo vacía en 6 horas. ¿En cuánto tiempo se llenará el tanque si la llave del desagüe empieza a funcionar una hora después de abierto el caño? | ||
| |url1=https://www.youtube.com/watch?v=u6nsbjY0Vy8 | |url1=https://www.youtube.com/watch?v=u6nsbjY0Vy8 | ||
| }} | }} | ||
| + | |||
| ==Cronometría== | ==Cronometría== | ||
| {{Videotutoriales|titulo=Problemas de cronometría|enunciado= | {{Videotutoriales|titulo=Problemas de cronometría|enunciado= | ||
| Línea 306: | Línea 264: | ||
| |sinopsis=Problemas de cronometría | |sinopsis=Problemas de cronometría | ||
| |url1=https://www.youtube.com/watch?v=Tn4ff5b4qUM&index=35&list=PL3KGq8pH1bFTEqvQj6O_p10Kc0oTP4nb2 | |url1=https://www.youtube.com/watch?v=Tn4ff5b4qUM&index=35&list=PL3KGq8pH1bFTEqvQj6O_p10Kc0oTP4nb2 | ||
| + | }} | ||
| + | }} | ||
| + | ==Combinatoria== | ||
| + | {{Videotutoriales|titulo=Problemas de combinatoria (diagramas de árbol)|enunciado= | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=3´01" | ||
| + | |sinopsis=Problema de combinatoria usando diagramas de árbol. | ||
| + | |url1=https://www.youtube.com/watch?v=IXhj3NLcbKY&list=PL2015DAE219999027 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=3´49" | ||
| + | |sinopsis=Problema de combinatoria usando diagramas de árbol. | ||
| + | |url1=https://www.youtube.com/watch?v=vfLF-TNIjE4&index=2&list=PL2015DAE219999027 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Problema 3 | ||
| + | |duracion=3´33" | ||
| + | |sinopsis=Problema de combinatoria usando diagramas de árbol. | ||
| + | |url1=https://www.youtube.com/watch?v=Qxcno5UKqwg&list=PL2015DAE219999027&index=3 | ||
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Aritmética]] | [[Categoría: Matemáticas]][[Categoría: Aritmética]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 47)
Repartos proporcionales
En los repartos proporcionales tenemos que partir una cantidad en varias partes, de manera que cada parte sea proporcional, directa o inversamente, a unos ciertos números dados.
Repartos directamente proporcionales
Procedimiento
Para repartir una cantidad, 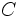 , en partes directamente proporcionales a
, en partes directamente proporcionales a 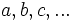 , tenemos que:
, tenemos que:
- Calcular la suma
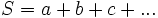 y la razón
y la razón 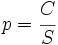 .
.
- Multiplicar
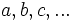 por
por 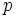 para obtener las partes buscadas:
para obtener las partes buscadas: 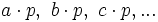
Ejemplo: Repartos directamente proporcionales
Tres grifos aportan 2 l/s, 5 l/s y 7 l/s, respectivamente. Se abren los tres simultáneamente para llenar una balsa de 17080 l. Cuando la balsa está llena, ¿qué volumen de agua habrá manado de cada grifo?
Los tres grifos aportan 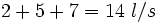 , de manera que:
, de manera que:
El primero aporta 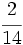 del total
del total 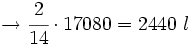
El segundo aporta 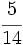 del total
del total 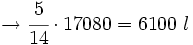
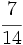 del total
del total 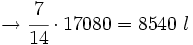
Tutorial que explica los problemas de reparto proporcional.
Tutorial que explica un problema concreto de proporcionalidad directa que es el de un reparto, viendo distintos métodos de resolución: por proporciones/porcentajes, reducción a la unidad, proporcionalidad y regla de tres:
Problema: Tres amigos, Ana, Berta y Carlos, decidieron echar una quiniela de futbol poniendo cada uno de ellos, 6, 15 y 9 €, respectivamente. Después del fin de semana se enteraron que habían tenido 12 aciertos y que les había tocado un premio total de 1200 €. ¿Cuánto dinero le corresponderá a cada uno de ellos?
Reparto proporcional directo:
- La comunidad de una urbanización encarga su pintado a tres empresas. La empresa A pinta 50 pisos, la B, 39, y la C, 51. El coste del pintado asciende a 70000€. ¿Cuánto ha cobrado cada empresa?
- Tres amigos deciden formar una peña de apuestas deportivas. Pedro aporta 45 €, Laura 31 € y Agustín 44 €. En una apuesta ganan 55000 € y deciden repartirlo. ¿Cuánto le corresponde a cada uno?
Reparto proporcional directo:
Tres amigos compran lotería por valor de 20$. El primero pone 6$, el segundo 9$ y el tercero 5$. Si ganan un premiode 4000$, ¿cuánto le corresponde a cada uno?
2 ejemplos de problemas de repartos proporcionales.
Practica los repartos directamente proporcionales.
Problemas de autoevaluación sobre repartos directamente proporcionales.
Problemas de autoevaluación sobre repartos directamente proporcionales.
Repartos inversamente proporcionales
Procedimiento
Repartir una cantidad, 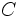 , en partes inversamente proporcionales a
, en partes inversamente proporcionales a  , equivale a repartir dicha cantidad en partes directamente proporcionales a sus inversos,
, equivale a repartir dicha cantidad en partes directamente proporcionales a sus inversos, 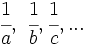
Ejemplo: Repartos inversamente proporcionales
Un jefe decide repartir 700 € de gratificación entre sus tres empleados, Juan, Luis y Guillermo, de manera que cada uno reciba una cantidad que sea inversamente proporcional al número de veces que han llegado tarde. Si Juan ha llegado 1 día tarde, Luis, 2 días, y Guillermo, 4 días, cuánto le corresponderá a cada uno?
hay que hacer un reparto directamente proporcional a 1, 1/2 y 1/4:
Calculamos 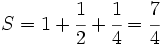 y
y 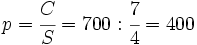
Juan recibirá 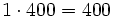 €.
€.
Luis recibirá 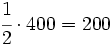 €.
€.
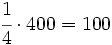 €.
€.Tutorial que explica los problemas de repartos inversamente proporcionales.
Tutorial que explica un problema concreto de reparto proporcional inverso.
Problema: Tres amigos, Ana, Berta y Carlos, decidieron echar una carrera, en la cual tardaron 2, 3 y 4 minutos, respectivamente. Antes de la misma, acordaron repartirse 390 cromos de una colección en función del tiempo empleado en la carrera. ¿Cuántos cromos le corresponden a cada uno de ellos?
Reparto proporcional inverso:
Se va a repartir una gratificación por puntualidad consistente en 38$, entre 3 empleados de una oficina. Sabiendo que han tenido 2, 4 y 5 retrasos, respectivamente, ¿cuánto dinero recibe cada uno?
Problemas de repartos inversamente proporcionales.
Practica los repartos inversamente proporcionales.
Problemas de autoevaluación sobre repartos inversamente proporcionales.
Problemas de autoevaluación sobre repartos inversamente proporcionales.
Actividades
Practica con problemas de repartos proporcionales directos e inversos.
Problemas resueltos sobre repartos proporcionales.
|
Ejercicios propuestos: Repartos proporcionales |
(Pág. 48)
Mezclas
Ejercicio resuelto: Mezclas
Se muelen conjuntamente 50 kg de café de 8.80 €/kg y 30 kg de otro café de inferior calidad, de 6.40 €/kg. ¿A cómo resulta el kilo de la mezcla obtenida?
Para resolverlo haremos uso de la siguiente tabla:
| 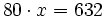
|
Problema de mezclas con sales de baño.
Se dispone de dos clase de café: uno de 1.05$ y otro de 1.25$ la libra. ¿Qué cantidad se utiliza de cada uno para obtener café de 1.20$ la libra, si de la clase más cara se utilizan 20 libras más que de la barata?
¿Cuántos litros de una solución de alcohol al 30% deben mezclarse con 90 litros de otra solución al 70% para obtener una solución al 60%?
Si tienes 50 onzas de una solución salina al 25% (mezcla de agua con sal), ¿Cuántas onzas de solución salina al 10% debes agregar para obtener una nueva solución salina al 15%?
Un biólogo realiza una investigación sobre el impacto de tres diferentes bebidas azucaradas a base de agua en la habilidad de las abejas de producir miel. Coge 2 litros de la bebida A, que contiene 40% de azúcar, y agrega 1.2 litros de bebida B. Comprobó que las abejas preferían esta nueva solución, que llamaremos bebida C, la cual medimos que contiene 25% de azúcar. ¿Cuál es el porcentaje de azúcar de la bebida B?
|
Ejercicios propuestos: Mezclas |
(Pág. 49)
Móviles
A tener en cuenta ...
- Dos móviles que van uno al encuentro del otro, se aproximan con una velocidad relativa igual a la suma de las velocidades absolutas de cada móvil.
- Dos móviles que van uno en persecusión del otro, se aproximan con una velocidad relativa igual a la diferencia de las velocidades absolutas de cada móvil.
Ejercicios resueltos: Móviles
1. Un ciclista profesional, entrenándose, avanza por una carretera a una velocidad de 38 km/h. Más adelante, a 22 km, un cicloturista avanza en el mismo sentido a 14 km/h. ¿Cuánto tarda el ciclista profesional en alcanzar al cicloturista?
2. Un motorista y un coche avanzan por una carretera, dirigiéndose el uno hacia el otro, a unas velocidades de 50 km/h y 100 km/h, respectivamente. Si los separa una distancia de 10 km, ¿cuánto tiempo tardarán en encontrarse?
Solución 1: Los ciclistas se aproximan a una velocidad de 38 - 14 = 24 km/h.
Calculamos el tiempo hasta que se encuentran, sabiendo que les separan 22 km:
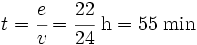
Solución 2:
Los dos se aproximan a una velocidad de 50 + 100 = 150 km/h.
Calculamos el tiempo hasta que se encuentran, sabiendo que les separan 10 km:
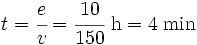
Problemas de móviles:
- Dos ciudades A y B distan 90 km. Un coche sale de A hacia B a las 9 de la mañana a 70 km/h. Al mismo tiempo, un camión sale de B hacia A a 50 km/h. ¿A qué distancia de A se cruzan? ¿A qué hora?
- Dos ciudades A y B distan 250 km. Un coche sale de A hacia B a las 9 de la mañana a 70 km/h. Una hora más tarde, un camión sale de B hacia A a 50 km/h. ¿A qué distancia de A se cruzan? ¿A qué hora?
Problema de móviles:
Un camión sale de una ciudad A a las 9 de la mañana a 50 km/h. Una hora más tarde sale un coche en su persecución a 70 km/h. ¿A qué distancia de A se encuentran? ¿A qué hora?
Problemas de móviles.
Problemas de móviles.
Problemas de móviles.
Problemas de móviles.
Problemas de móviles.
Problemas de móviles.
Problemas de móviles.
|
Ejercicios propuestos: Móviles |
Grifos
Un grifo tarda 4h en llenar un recipiente y a otro le cuesta 12h. ¿Cuánto tardaremos si abrimos los dos grifos a la vez?
Tres grifos tardan 2h y 40min en llenar una piscina. Sabiendo que uno de ellos lo hace en solo 6h y el otro en 8h, ¿cuánto tardará el tercero?
Problema de grifos.
Problemas de grifos.
Problemas de grifos.
Un caño llena un tanque en 4 horas y un desagüe lo vacía en 6 horas. ¿En cuánto tiempo se llenará el tanque si la llave del desagüe empieza a funcionar una hora después de abierto el caño?
Cronometría
Problemas de cronometría
Problemas de cronometría
Problemas de cronometría
Problemas de cronometría
Problemas de cronometría
Combinatoria
Problema de combinatoria usando diagramas de árbol.
Problema de combinatoria usando diagramas de árbol.
Problema de combinatoria usando diagramas de árbol.