Números reales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 13:00 29 jul 2007 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los reales) ← Ir a diferencia anterior |
Revisión de 13:03 29 jul 2007 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los reales) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| ==Orden en el conjunto de los reales== | ==Orden en el conjunto de los reales== | ||
| - | {{Caja_Amarilla|texto=Dados dos números reales a y b, se dice que '''a es menor que b''', <math>a<b</math>, si b está más a la derecha que a en la recta real, o dicho de otra forma, si b-a es positivo <math>b-a> 0</math> | + | {{Caja_Amarilla|texto=Dados dos números reales <math>a\;\!</math> y <math>b\;\!</math>, se dice que '''<math>a\;\!</math> es menor que <math>b\;\!</math>''', <math>a<b\;\!</math>, si <math>b\;\!</math> está más a la derecha que <math>a\;\!</math> en la recta real, o dicho de otra forma, si b-a\;\! es positivo <math>b-a>0\;\!</math>}} |
Revisión de 13:03 29 jul 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Números reales
Los números racionales y los irracionales forman el conjunto de los números reales y se designa con la letra 
Representación de los números reales
Cuando en una recta se representan los números racionales e irracionales se obtiene la recta real. Cualquier punto de la recta real representa un número real. .
|
Actividad Interactiva: Representación de los números reales
Actividad 1. Representación gráfica de los números reales en la recta real.
Actividad: Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas. Luego introduce distintos número y observa su representación en la recta real:
|
Orden en el conjunto de los reales
Dados dos números reales  y
y  , se dice que
, se dice que  es menor que
es menor que  ,
, 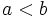 , si
, si  está más a la derecha que
está más a la derecha que  en la recta real, o dicho de otra forma, si b-a\;\! es positivo
en la recta real, o dicho de otra forma, si b-a\;\! es positivo 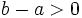
 (teclea a/b para introducir la fracción
(teclea a/b para introducir la fracción  )
)

