Números racionales: Operaciones
De Wikipedia
| Revisión de 11:23 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:36 7 ago 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 184: | Línea 184: | ||
| }} | }} | ||
| }} | }} | ||
| + | ==La fracción como operador== | ||
| + | {{Caja_Amarilla|texto=Para calcular una fracción <math>\cfrac {a}{b}</math> de una cantidad <math>C\;\!</math>, procedermos multiplicando la fracción por la cantidad <math>C\;\!</math>: | ||
| + | <center><math>P=\cfrac {a}{b} \cdot C</math></center> | ||
| + | }}{{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejemplo: ''La fracción como operador'' | ||
| + | |enunciado= | ||
| + | :De una herencia de 27 millones de euros, María recibe las tres quintas partes, su hermano Ramón, la mitad del resto, y su hermana Matilde, lo que queda. | ||
| + | ::a) ¿Qué fracción le corresponde a cada uno? | ||
| + | ::b) Calcula cuánto se lleva cada uno. | ||
| + | |sol= | ||
| + | a) Calculamos la fracción que se cada uno: | ||
| + | *María recibe: <math>\cfrac{3}{5}</math> | ||
| + | *Ramón recibe: <math>\cfrac{1}{2} \cdot \cfrac{2}{5}=\cfrac{1}{5}</math> | ||
| + | *Matilde recibe: <math>1-(\cfrac{3}{5}+\cfrac{1}{5})=1-\cfrac{4}{5}=\cfrac{1}{5}</math> | ||
| + | |||
| + | b) Calculamos cuántos euros se lleva cada uno: | ||
| + | |||
| + | *María recibe: <math>\cfrac{3}{5} \cdot 27=\cfrac{3 \cdot 27}{5}=\cfrac{81}{5}</math> € | ||
| + | *Ramón recibe: <math>\cfrac{1}{5} \cdot 27=\cfrac{27}{5}</math> € | ||
| + | *Matilde recibe: <math>\cfrac{1}{5} \cdot 27=\cfrac{27}{5}</math> € | ||
| + | }} | ||
| + | {{p}} | ||
| ==Ejercicios== | ==Ejercicios== | ||
| {{ejercicio | {{ejercicio | ||
| Línea 198: | Línea 221: | ||
| a) <math>-\cfrac{1}{6}</math>{{b}}b) <math>\cfrac{4}{3}</math>{{b}}c) <math>-\cfrac{13}{32}</math> | a) <math>-\cfrac{1}{6}</math>{{b}}b) <math>\cfrac{4}{3}</math>{{b}}c) <math>-\cfrac{13}{32}</math> | ||
| + | }} | ||
| }} | }} | ||
Revisión de 11:36 7 ago 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
Operaciones con fracciones
Suma y resta de fracciones
Para sumar o restar fracciones:
- Si las fracciones tienen el mismo denominador, se suman o restan los numeradores y se pone el mismo denominador.
- Si tienen distintos denominadores, primero se reducen a común denominador y luego se procede como en el caso anterior.
Ejemplo: Suma y resta de fracciones
- Calcula:
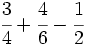
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
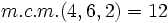 .
.
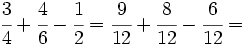
Luego sumamos o restamos los númeradores, dejando el mismo denominador:
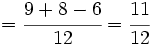
|
Actividad Interactiva: ''Suma y resta de fracciones
Actividad 1: Aprende a sumar y restar fracciones.
Actividad: Cuando tenemos juntas sumas y restas seguimos el mismo proceso que si tuviéramos solamente sumas. Para sumar y restar fracciones es necesario que tengan todas el mismo denominador. Si las fracciones tienen distintos denominadores se pasan a común denominador, es decir, se cambian por otras equivalentes a ellas pero con el mismo denominador todas. Para ello se siguen estos pasos:
En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Realiza las siguientes sumas y restas de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
Multiplicación de fracciones
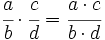
Ejemplo: Producto de fracciones
- Calcula:
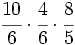
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto:
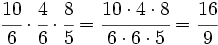
|
Actividad Interactiva: ''Producto de fracciones
Actividad 1: Aprende a multiplicar fracciones.
Actividad: Para multiplicar fracciones no hace falta pasarlas a común denominador, se multiplican directamente. Multiplicamos sus numeradores y lo ponemos de numerador, multiplicamos sus denominadores y lo ponemos de denominador. A continuación se simplifican. No obstante, es conveniente simplificar antes de multiplicar. En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Realiza las siguientes multiplicaciones de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
Inversa de una fracción
Dada una fracción 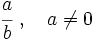 , su inversa es la fracción
, su inversa es la fracción 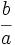 .
.
Por ejemplo, la inversa de 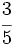 es
es 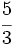 .
.
|
Actividad Interactiva: Inversa de una fracción
Actividad 1: Halla la fracción inversa de una fracción.
Actividad: La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa. Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados. Pulsa "inicio" para que aparezca otra fracción. |
División de fracciones
Para dividir dos fracciones, se pone como numerador, el producro del primer numerador por el segundo denominador, y como denominador, el producto del primer denominador por el segundo numerador.
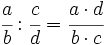
Ejemplo: Cociente de fracciones
- Calcula:
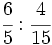
Multiplicamos en cruz, simplificando antes de efectuar el producto:
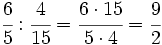
|
Actividad Interactiva: Cociente de fracciones
Actividad 1: Aprende a dividir fracciones.
Actividad: Dividir una fracción por otra es lo mismo que multiplicar la primera fracción por la inversa de la segunda fracción. Una fracción se puede dividir por cualquier otra, menos por la fracción 0. Haz la división en tu cuaderno y luego comprueba el resultado, viendo el desarrollo paso a paso. Para ello pulsa la flecha azul. Pulsa "inicio" para que aparezca otra fracción. |
La fracción como operador
Para calcular una fracción  de una cantidad
de una cantidad 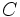 , procedermos multiplicando la fracción por la cantidad
, procedermos multiplicando la fracción por la cantidad 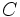 :
:
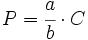
Ejemplo: La fracción como operador
- De una herencia de 27 millones de euros, María recibe las tres quintas partes, su hermano Ramón, la mitad del resto, y su hermana Matilde, lo que queda.
- a) ¿Qué fracción le corresponde a cada uno?
- b) Calcula cuánto se lleva cada uno.
a) Calculamos la fracción que se cada uno:
- María recibe:
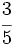
- Ramón recibe:
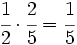
- Matilde recibe:
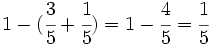
b) Calculamos cuántos euros se lleva cada uno:
- María recibe:
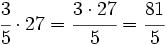 €
€
- Ramón recibe:
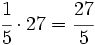 €
€
- Matilde recibe:
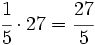 €
€
Ejercicios
|
Ejercicios: Operaciones con fracciones 1. Opera las fracciones:
Solución: a) 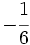 b) b) 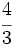 c) c) 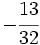 |
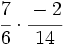 b)
b) 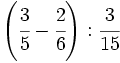 c)
c)