Números racionales: Operaciones
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Fracciones IV | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
Suma y resta de fracciones
Procedimiento: Suma de fracciones
Para sumar o restar fracciones:
- Si las fracciones son homogéneas (mismo denominador), se suman o restan los numeradores y se deja el mismo denominador.
- Si son heterogéneas (distinto denominador), primero se reducen a común denominador y luego se procede como en el caso anterior.
Si en una suma de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
Cuando hagamos operaciones con fracciones, no sólo la suma y la resta, es posible que el resultado sea una fracción que se pueda simplificar. Es importante que te acostumbres a simplificar el resultado todo lo que sea posible. En la Fig.1, por ejemplo, el resultado que deberíamos dar es 3/4 en lugar de 6/8.
Ejemplo: Suma y resta de fracciones
Calcula: 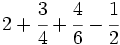
Solución:
Tenemos que calcular:
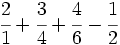
Calculamos el m.c.m. de los denominadores:
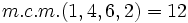
y reducimos las fracciones a común denominador:
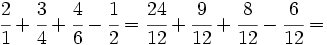
Una vez que tenemos las fracciones homogéneas, sumamos o restamos los númeradores, dejando el mismo denominador:
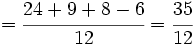
- Suma y resta de fracciones con el mismo denominador.
- Suma y resta de fracciones con el distinto denominador.
- Ejemplos.
Tutorial que explica la suma y resta con fracciones de igual denominador de distintos denominadores y con paréntesis.
- Suma de fracciones con el mismo o con distinto denominador.
- Ejemplos.
- Propiedades.
Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma de fracciones con el mismo denominador.
Resta de fracciones con el mismo denominador.
Suma de fracciones mixtas con el mismo denominador.
Resta de fracciones mixtas con el mismo denominador.
Suma y resta de fracciones con el mismo denominador:
a) 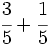 b)
b) 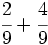 c)
c) 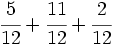 d)
d) 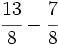 e)
e) 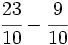
Suma y resta de fracciones con el mismo denominador.
Suma de fracciones usando el método gráfico.
Resta de fracciones usando el método gráfico.
Suma de fracciones usando el método del m.c.m.
Resta de fracciones usando el método del m.c.m.
Suma de números mixtos usando el método del m.c.m.
Resta de números mixtos usando el método del m.c.m.
Suma y resta de fracciones usando el método del m.c.m.
Otro método para sumar o restar fracciones, fácil de recordar, que no requiere del m.c.m, pero que a veces precisa simplificar más al final. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma y resta de fracciones con distinto denominador (método rápido) Suma y resta de fracciones con distinto denominador (método del m.c.m.): a) Suma de fracciones con distinto denominador (método rápido): a) b) Resta de fracciones con distinto denominador (método rápido): a) b) Suma de fracciones con distinto denominador (método del m.c.m.): a) Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador:
Suma y resta de fracciones con distinto denominador (método rápido): | Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.): Suma de un entero y una fracción: Resta de un entero y una fracción. Suma de números mixtos. Resta de números mixtos. Suma y resta de números mixtos. Calcula: Calcula: |
Si Fernando recoge 3/4 de kilo de verdura y David recoge 1/8 de kilo de verdura, calcula los kilos de verdura que han recogido entre los dos e indica aquél que ha recogido menos cantidad.
Suma de fracciones por el método del m.c.m.
Suma y resta de fracciones por el método del m.c.m.
Suma y resta de fracciones. Propiedades.
Suma y resta de fracciones con o sin paréntesis.
Opuesta de una fracción
- Dos fracciones son opuestas cuando su suma es cero.
- Dada una fracción
 , su opuesta es la fracción
, su opuesta es la fracción 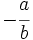 .
.
Multiplicación y división de fracciones
Videotutorial sobre la multiplicación y división de fracciones.
Tutorial que explica la multiplicación y división con fracciones de manera simple y en forma combinada, trabajando la simplificación previa.
Actividades en las que aprenderás la multiplicación de fracciones y sus propiedades.
Multiplicación de fracciones
Procedimiento: Multiplicación de fracciones
Para multiplicar fracciones, se pone como numerador, el producto de los numeradores, y como denominador, el producto de los denominadores.
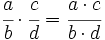
- Si en una multiplicación de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para multiplicar números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, la forma en que se realiza el producto de dos fracciones permite, en ocasiones, simplificar antes de realizar las multiplicaciones de los numeradores y denominadores. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo: Multiplicación de fracciones
Calcula: 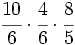
Solución:
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto: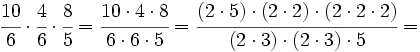
Aprende a multiplicar fracciones.
Aprende a multiplicar fracciones.
Aprende a multiplicar números naturales por fracciones.
Significado gráfico de la multiplicación de dos fracciones.
Representación en la recta numérica de la multiplicación de dos fracciones.
Aprende a multiplicar números por fracciones.
- Multiplicación de fracciones.
- Ejemplos.
- Propiedades.
Multiplica:
Multiplica:
a) 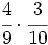 b)
b) 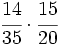 c)
c) 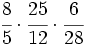
Multiplica un entero por una fracción:
a) 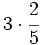
b) 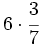
Multiplica fracciones mixtas con fracciones y enteros:
Multiplica:
Compara las siguientes fracciones sin hacer la multiplicación:
Multiplica:
Para elaborar cierto pastel, la receta dice que por cada libra se debe usar 1 taza y 3/4 de almendras. Si nos encargan un pastel de 3 libras y media, ¿cuántas tazas de almendras son necesarias?
Una receta para pastelillos de plátano y avena requiere 3/4 tazas de avena. Si preparamos 1/2 de la receta, ¿cuánta avena necesitaremos?
Gina tenía 2/3 de taza de detergente. Si usó la mitad el viernes para lavar todas sus sábanas, ¿Cuánto le sobra?.
Puedes andar en bicicleta 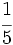 de milla por minuto. Si tardas
de milla por minuto. Si tardas 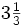 de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
Actividades en las que aprenderás y practicarás la multiplicación de fracciones.
Actividades para practicar la multiplicación de fracciones.
Inversa de una fracción
- Dos fracciones son inversas cuando su producro es la unidad.
- Toda fracción
 , distinta de cero, tiene inversa. Su inversa es la fracción
, distinta de cero, tiene inversa. Su inversa es la fracción 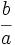 .
.
La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa.
Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados.
Pulsa "inicio" para que aparezca otra fracción.
División de fracciones
Procedimiento: División de fracciones
Para dividir dos fracciones, se multiplica la primera fracción por la inversa de la segunda.
El resultado es otra fracción, cuyo numerador, es el producto del primer numerador por el segundo denominador, y cuyo denominador es el producto del primer denominador por el segundo numerador.
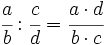
- Si en una división de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para dividir números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, al igual que ocurre con la multiplicación de fracciones, en ocasiones, podremos simplificar antes de efectuar los productos cruzados de los numeradores y denominadores. Lo que haremos es dejar indicados los productos cruzados y simplificarlos, si es posible, antes de multiplicarlos. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo:
Calcula: 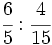
Solución:
Multiplicamos en cruz, simplificando antes de efectuar el producto:Aprende a dividir fracciones.
Aprende a dividir fracciones.
Aprende a dividir fracciones (2 métodos). Ejercicios propuestos y resueltos.
División de dos fracciones usando la fracción inversa. Ejemplos.
- División de fracciones.
- Ejemplos.
- Ejercicios con operaciones combinadas.
División de fracciones. Ejemplo.
Cómo se dividen las fracciones. Ejemplos.
Equivalencias fundamentales en la multiplicación y división de fracciones.
Fracciones de términos no enteros y fracciones de términos racionales
Simplificación de fracciones de términos racionales.
Las propiedades de la división de fracciones
Entendiendo el concepto de división de fracciones
Calcula:
Calcula y expresa la solución como un número mixto:
Calcula:
- 1)
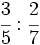 ; 2)
; 2) 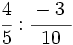 ; 3)
; 3) 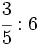 ; 4)
; 4) 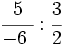
- 5)
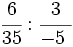 ; 6)
; 6) 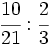 ; 7)
; 7) 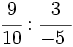
Calcula:
- 8)
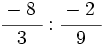 ; 9)
; 9) 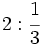 ; 10)
; 10) 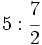
- 11)
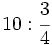 ; 12)
; 12) 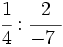 ; 13)
; 13) 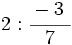
Corrige esta cuenta si crees que es incorrecta:
- 14)
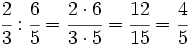
Calcula:
- 15)
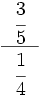 ; 16)
; 16)  ; 17)
; 17) 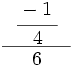 ; 18)
; 18) 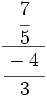
- 19)
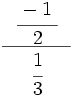 ; 20)
; 20) 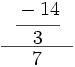 ; 21)
; 21) 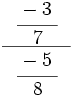
Calcula:
- 22)
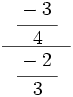 ; 23)
; 23) 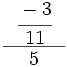 ; 24)
; 24) 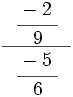
- 25)
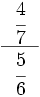 ; 26)
; 26) 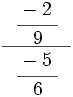 ; 27)
; 27) 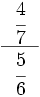
Escribe la fracción que falta para que se verifique la igualdad:
- 52)
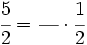
- 53)
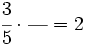
División de fracciones.
a) 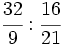 b)
b) 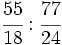
Divide un entero por una fracción:
Divide fracciones mixtas con fracciones:
En la fiesta de cumpleaños de Luisa ha sobrado 1/3 del pastel. Jaime lo ha visto y, como tenía hambre, se ha comido la mitad. ¿Qué parte o fracción de pastel se ha comido Jaime?. ¿Qué parte o fracción del pastel sobra?
La camiseta de un bebe se fabrica con 4/5 metros de tela. ¿Cuántas camisetas se pueden hacer con 48 metros de tela?
Actividades en las que aprenderás y practicarás la división de fracciones.
Actividades para practicar la división de fracciones.
Actividades para practicar la división de fracciones.
Potencia de una fracción
Procedimiento: Potencia de una fracción
Para elevar una fracción a una potencia se eleva el numerador y el denominador a dicha potencia.
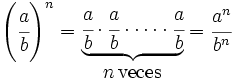
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
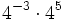
- b)
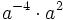
- c)
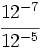
- d)
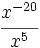
Simplifica:
- a)
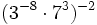
- b)
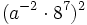
- c)
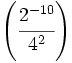
Halla el valor de:
11) 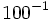 ; 12)
; 12) 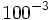 ; 13)
; 13) 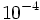 ; 14)
; 14) 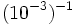
15) 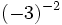 ; 16)
; 16) 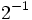 ; 17)
; 17) 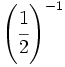 ; 18)
; 18) 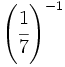 ; 19)
; 19) 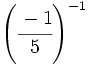
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 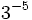 b)
b) 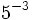 c)
c) 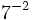 d)
d) 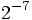
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
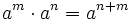
- 2. Cociente de potencias de la misma base:
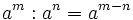
- 3. Potencia de un producto:
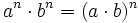
- 4. Potencia de un cociente:
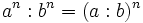
- 5. Potencia de otra potencia:
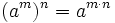
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 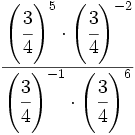
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejemplos: Potencias de fracciones
Calcula simplificando previamente:
a) 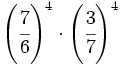 b)
b) 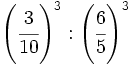 c)
c) 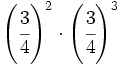
d) 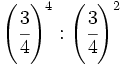 e)
e) 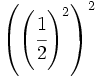 f)
f) 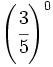
a)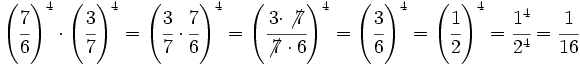
b)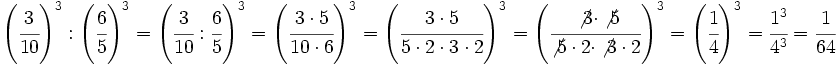
c)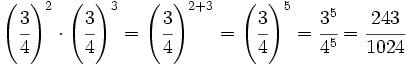
d)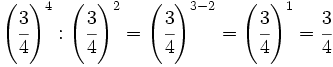
e) 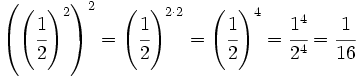
f)
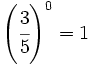
Ejercicios de autoevaluación sobre potencias de fracciones.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Ejercicios de autoevaluación sobre potencias de números racionales.
Raíces de fracciones
Cómo se calculan las raíces de fracciones. Ejemplos.
Cómo se suman y restan las raíces de fracciones. Ejemplos.
Cómo se multiplican raíces de fracciones. Ejemplos.
Cómo se dividen raíces de fracciones. Ejemplos.
Cómo se calculan las potencias de raíces de fracciones. Ejemplos.
Cómo se calculan las raíces de raíces de fracciones. Ejemplos.
Suma y resta de raíces de fracciones:
- 1)
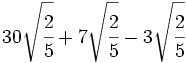
- 2)
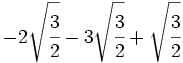
- 3)
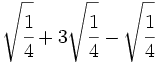
- 4)
![-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/f/5/5/f55a7abe041410d0d772b3f5f9249888.png)
- 5)
![-8\sqrt[3]{\cfrac{-3}{5}}+\cfrac{3}{2}\sqrt[3]{\cfrac{-3}{5}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-3}{5}}](/wikipedia/images/math/c/7/e/c7e1346a8d6ef7ddeb7f7c7972383303.png)
Suma y resta de raíces de fracciones:
- 6)
![\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+2\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/e/7/4/e74f2414908471712a21bcd2c0727973.png)
- 7)
![\sqrt[8]{\cfrac{9}{4}}+12\sqrt[8]{\cfrac{9}{4}}-\cfrac{1}{4}\sqrt[8]{\cfrac{9}{4}}](/wikipedia/images/math/7/9/5/7956651986adce493726a51fce226382.png)
- 8)
![\cfrac{-1}{3}\sqrt[11]{\cfrac{-3}{7}}+\cfrac{1}{9}\sqrt[11]{\cfrac{-3}{7}}-\cfrac{2}{3}\sqrt[11]{\cfrac{-3}{7}}](/wikipedia/images/math/f/c/e/fceb6863061e8ca281259ac86890e169.png)
- 9)
![-\sqrt[5]{\cfrac{5}{3}}-\cfrac{5}{2}\sqrt[5]{\cfrac{5}{3}}-\cfrac{1}{4}\sqrt[5]{\cfrac{5}{3}}](/wikipedia/images/math/9/2/2/92245797897977068795b35dc3cbcfc7.png)
Multiplicaciones de raíces de fracciones:
- 10)
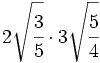
- 11)
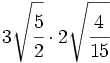
- 12)
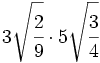
- 13)
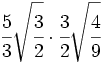
Multiplicaciones de raíces de fracciones:
- 14)
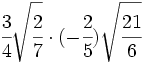
- 15)
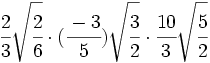
- 16)
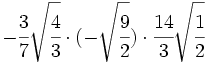
Multiplicaciones de raíces de fracciones:
- 17)
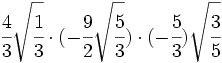
- 18)
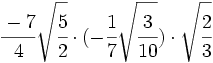
- 19)
![2\sqrt[3]{\cfrac{2}{5}} \cdot 3\sqrt[3]{\cfrac{4}{25}}](/wikipedia/images/math/f/8/1/f81614b373a70320fa5bbee491ded79d.png)
- 20)
![\sqrt[3]{\cfrac{9}{2}} \cdot \cfrac{5}{6}\sqrt[3]{\cfrac{2}{125}}](/wikipedia/images/math/f/d/b/fdbcdfd572102f2971190e92ad2b9ca8.png)
Multiplicaciones de raíces de fracciones:
- 21)
![\cfrac{-2}{5}\sqrt[3]{\cfrac{-1}{3}} \cdot 5\sqrt[3]{\cfrac{-1}{9}}](/wikipedia/images/math/e/1/d/e1dc683585b12c3e8f8b0336e6cd3dce.png)
- 22)
![2\sqrt[3]{\cfrac{7}{3}} \cdot \cfrac{1}{4}\sqrt[3]{\cfrac{9}{14}}](/wikipedia/images/math/4/e/5/4e5561c3d3d0f4cadb26ebea76193f5e.png)
- 23)
![8\sqrt[3]{\cfrac{3}{7}} \cdot \sqrt[3]{\cfrac{-7}{9}} \cdot \sqrt[3]{\cfrac{-7}{2}}](/wikipedia/images/math/9/9/9/99904e001c4c05d9a33cc7f20320c6eb.png)
Multiplicaciones de raíces de fracciones:
- 24)
![3\sqrt[3]{\cfrac{9}{4}} \cdot \left( -\cfrac{1}{2}\sqrt[3]{\cfrac{3}{2}} \right) \cdot \cfrac{2}{5}\sqrt[3]{125}](/wikipedia/images/math/d/3/c/d3cb69b0f72a7fed15f71aa8513dfbb6.png)
- 25)
![\cfrac{4}{3}\sqrt[4]{\cfrac{3}{7}} \cdot 3\sqrt[4]{\cfrac{16}{3}}](/wikipedia/images/math/b/d/5/bd5b5b76b496c2f6825e62489c158052.png)
- 26)
![\cfrac{1}{3}\sqrt[8]{\cfrac{1}{4}} \cdot \left( -\cfrac{9}{2}\sqrt[8]{\cfrac{2}{3}} \right) \cdot 4\sqrt[8]{\cfrac{3}{5}}](/wikipedia/images/math/7/4/4/74408c6f3e91a102054dcf8b4a208595.png)
División de raíces de fracciones:
- 27)
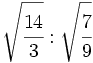
- 28)
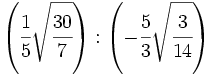
- 29)
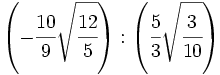
- 30)
![\left( -\cfrac{2}{3}\sqrt[3]{\cfrac{14}{5}} \right): \left( \cfrac{14}{12}\sqrt[3]{\cfrac{7}{10}} \right)](/wikipedia/images/math/a/9/1/a913d1108fd67aec4f52e62b81efa9e8.png)
División de raíces de fracciones:
- 31)
![\left( \cfrac{9}{2}\sqrt[3]{\cfrac{14}{9}} \right) : \left( \sqrt[3]{\cfrac{-7}{3}} \right)](/wikipedia/images/math/8/9/e/89e41ac40d647d9d9d10fd9f080b8f9c.png)
- 32)
![\left( \cfrac{12}{5}\sqrt[3]{\cfrac{18}{3}} \right): \left( -\cfrac{6}{5}\sqrt[3]{\cfrac{-9}{2}} \right)](/wikipedia/images/math/7/8/b/78b4e0f5d87c167f3b7d0e410f45c6ec.png)
División de raíces de fracciones:
- 33)
![\left( -\cfrac{10}{3}\sqrt[4]{\cfrac{15}{49}} \right) : \left( \cfrac{5}{27}\sqrt[4]{\cfrac{49}{125}} \right)](/wikipedia/images/math/a/6/4/a64ae58b74db2719880d0c4bceb986c7.png)
- 34)
![\left( -\cfrac{10}{4}\sqrt[5]{\cfrac{15}{7}} \right): \left( \cfrac{5}{6}\sqrt[5]{\cfrac{5}{14}} \right)](/wikipedia/images/math/9/4/7/9479dbe129a893330d386ef04c8dddcb.png)
- 35)
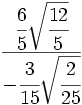
División de raíces de fracciones:
- 36)
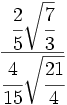
- 37)
![\cfrac{-\cfrac{10}{7}\sqrt[3]{\cfrac{15}{4}}}{5\sqrt[3]{\cfrac{8}{9}}}](/wikipedia/images/math/3/f/7/3f7ec32f3c77881d616b8760375d4d6f.png)
- 38)
![\cfrac{-\cfrac{10}{6}\sqrt[3]{\cfrac{15}{4}}}{\cfrac{5}{3}\sqrt[3]{\cfrac{2}{25}}}](/wikipedia/images/math/2/f/5/2f578dac94a33d0ddc501f0c60f4fffb.png)
Potencias de raíces de fracciones:
- 39)
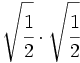
- 40)
![\sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}}](/wikipedia/images/math/6/3/9/63995d3707778bdb86de378c75aca586.png)
- 41)
![\sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}}](/wikipedia/images/math/6/3/3/633c62efe0db98851d8196c7d058cbe0.png)
- 42)
![\sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}}](/wikipedia/images/math/9/0/e/90e63a779d9f738b1332ad73f20d0c44.png)
- 43)
![\sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}}](/wikipedia/images/math/9/f/0/9f0f9afc0dba273231a5b490e098027d.png)
Convierte en potencias de exponente fraccionario:
- 44)
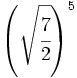 ; 45)
; 45) 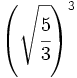 ; 46)
; 46) 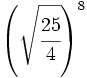
- 47)
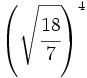 ; 48)
; 48) 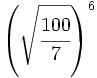 ; 49)
; 49) ![\left( \sqrt[3]{\cfrac{7}{3}} \right)^6](/wikipedia/images/math/7/6/3/763844586d27849f01b0f220f197d4d0.png)
- 50)
![\left( \sqrt[3]{\cfrac{5}{2}} \right)^9](/wikipedia/images/math/5/b/7/5b7af58a06ea229f4169c8f038eeb6a0.png) ; 51)
; 51) ![\left( \sqrt[4]{\cfrac{7}{4}} \right)^8](/wikipedia/images/math/0/e/0/0e0e0fafb99b320da94e2293f4f14701.png) ; 52)
; 52) ![\left( \sqrt[6]{\cfrac{21}{5}} \right)^{12}](/wikipedia/images/math/a/0/7/a07d93d0c3029249c9933a99a2eb2728.png)
- 53)
![\left( \sqrt[21]{\cfrac{12}{5}} \right)^{14}](/wikipedia/images/math/5/5/3/55309d54139afb8fbea7172261e4f109.png)
Convierte la potencia en raíz:
- 54)
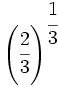 ; 55)
; 55) 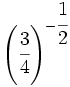 ; 56)
; 56) 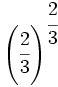
- 57)
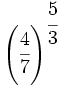 ; 58)
; 58) 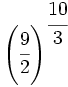 ; 59)
; 59) 
Raíces de una raíz de una fracción:
- 60)
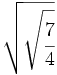 ; 61)
; 61) 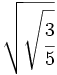 ; 62)
; 62) 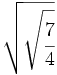
- 63)
![\sqrt[3]{\sqrt{\cfrac{2}{5}}}](/wikipedia/images/math/f/e/9/fe9d5ed19933ef100bc8b0f67559fa52.png) ; 64)
; 64) ![\sqrt[3]{\sqrt[3]{\cfrac{25}{4}}}](/wikipedia/images/math/7/b/3/7b3a4b58a2b91246bf250ff1abd743b3.png) ; 65)
; 65) ![\sqrt{\sqrt[3]{64}}](/wikipedia/images/math/0/e/d/0eddc7f2593e00fd623113cf77aff52f.png)
- 66)
![\sqrt[4]{\sqrt[3]{\cfrac{2}{7}}}](/wikipedia/images/math/e/b/e/ebedfae4b0471be70ea604bbe26e5e19.png) ; 67)
; 67) ![\sqrt[3]{\sqrt{\cfrac{12}{5}}}](/wikipedia/images/math/2/f/5/2f5c1b5dfc0e771272ee1b0c8e2ac6db.png)
Racionalización
Ver: Racionalización
Operaciones combinadas con fracciones
A la hora de operar con fracciones seguiremos las mismas pautas que con números enteros:
Ver: Jerarquía de las operaciones con números enteros
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Ejemplo:
Efectúa las siguientes operaciones combinadas:
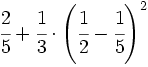
Solución:
- Los paréntesis:
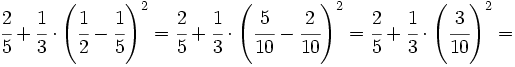
- Las potencias:

- Las multiplicaciones y divisiones:
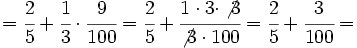
- Las sumas y restas:
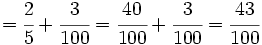
- Finalmente simplificaríamos si pudiésemos. En este caso la fracción es irreducible.
Tutorial que explica las operaciones combinadas con fracciones, señalando el orden que hay que seguir a la hora de realizar las operaciones con números (jerarquía de operaciones).
- 00:00 a 03:28: Conceptos básicos. Jerarquía de operaciones.
- 03:28 a 20:35: 7 Ejercicios de operaciones combinadas.
Operaciones combinadas con fracciones.
Operaciones combinadas con fracciones.
Operaciones combinadas con fracciones.
Opera y simplifica: 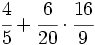
Opera y simplifica: 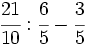
Opera y simplifica:
- a)
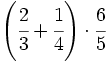
- b)
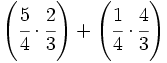
Calcula:
28) 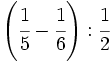
29) 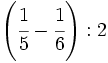
Calcula:
30) 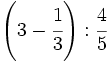
31) 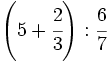
Calcula:
32) 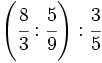
33) 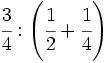
34) 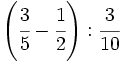
Calcula:
35) 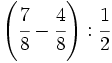
36) 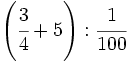
Calcula:
37) 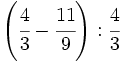
38) 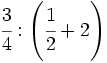
Calcula:
39) 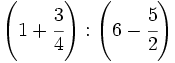 ; 40)
; 40) 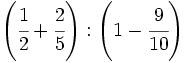 ; 41)
; 41) 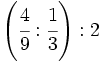
42) 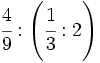 ; 43)
; 43) 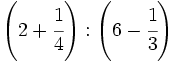
Opera y simplifica: 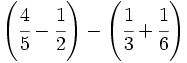
Opera y simplifica: 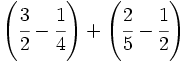
Opera y simplifica números mixtos: 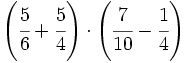
Opera y simplifica: 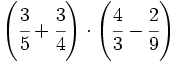
Opera y simplifica: 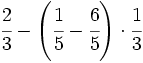
Operaciones combinadas con 3 fracciones sin paréntesis.
Operaciones combinadas con 4 fracciones con o sin paréntesis.
Multiplicaciones, divisiones y operaciones combinadas de fracciones.
Opera y simplifica: ![12- 6 \cdot \left[ \cfrac{1}{3}+\cfrac{5}{7} \left( \cfrac{2}{5}+ \cfrac{3}{10} \right)-2 \right]](/wikipedia/images/math/d/8/a/d8a9f0817768082ad4b67912b5ed86f4.png)
Opera y simplifica: ![\left(\cfrac{2}{5}-\cfrac{1}{2} \right)+ \cfrac{3}{5} \cdot \left[ \cfrac{7}{12}-\cfrac{3}{5} : \left( \cfrac{1}{4}- \cfrac{1}{5} \right) \right]](/wikipedia/images/math/d/7/4/d743f51542cc24868b95259918352133.png)
Opera y simplifica: 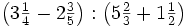
Opera y simplifica: ![\left[ 3 \left\{ 2(2-5)^2-4 \left(\frac{3}{2}-\cfrac{10}{4} \right)^3 \right \} + 3 \cdot \cfrac{7}{9} \right] - \sqrt{49}](/wikipedia/images/math/1/9/0/19095301a9dd1177e424b87facf98fed.png)
Tutorial que explica las operaciones con fracciones en las que intervienen "castillos".
Calcula:
- 44)
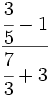 ; 45)
; 45) 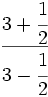 ; 46)
; 46) 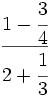
- 47)
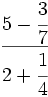 ; 48)
; 48) 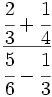
Calcula:
- 49)
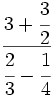 ; 50)
; 50) 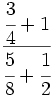 ; 51)
; 51) 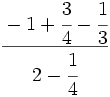
Opera y simplifica: 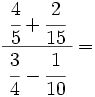
Opera y simplifica: 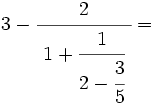
Opera y simplifica: 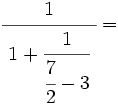
Opera y simplifica: 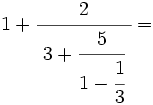
Opera y simplifica: 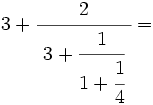
Opera y simplifica: 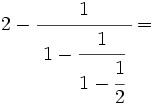
Opera y simplifica: 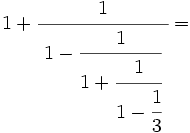
Actividades para aprender y practicar las operaciones combinadas con fracciones (Nivel 3).
Actividades para aprender y practicar las operaciones combinadas con fracciones.
Actividades para aprender y practicar las operaciones combinadas con fracciones. Incluye operaciones con paréntesis implícitos (castillos).
Ejercicios de autoevaluación sobre operaciones combinadas con fracciones.
Ejercicios de autoevaluación sobre operaciones combinadas con fracciones.
Nota: Esta actividad también incluye raíces de fracciones. En el siguiente enlace puedes ver acerca de ellas.
Potencias y raíces de fracciones
La fracción como operador
Para calcular una fracción  de una cantidad
de una cantidad 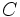 , procederemos multiplicando la fracción por la cantidad:
, procederemos multiplicando la fracción por la cantidad: 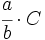
Ejemplo: La fracción como operador
- De una herencia de 27 millones de euros, María recibe las tres quintas partes, su hermano Ramón, la mitad del resto, y su hermana Matilde, lo que queda.
- a) ¿Qué fracción le corresponde a cada uno?
- b) Calcula cuánto se lleva cada uno.
a) Calculamos la fracción que se cada uno:
- María recibe:
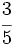
- Ramón recibe:
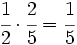
- Matilde recibe:
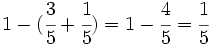
b) Calculamos cuántos euros se lleva cada uno:
- María recibe:
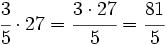 millones de €
millones de €
- Ramón recibe:
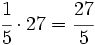 millones de €
millones de €
- Matilde recibe:
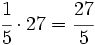 millones de €
millones de €
La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
Ejercicios
Problemas con fracciones.
Problemas con fracciones.
Problemas para practicar operaciones con fracciones
4 problemas:
- Una caja contiene 60 galletas. Raúl se come 1/3 y Manuel 2/5. ¿Cuántas galletas se ha comido cada uno?
- Pedro ha recorrido en bici 6 km, que son 3/4 de la etapa de hoy. ¿Cuál es el recorrido total de la etapa?
- Alicia tiene 30€ de paga mensual. La primera semana gastó 2/5. La segunda gastó 5/6 de lo que le quedaba. ¿Cuánto gastó cada semana?.¿Cuánto le queda?
- Tenemos que vaciar una piscina. Sacamos por la mañana 2/5 del agua y por la tarde 1/4 de lo que quedaba. Si la final del día había 180 litros, ¿cuál es la capacidad de la piscina?.
2 problemas:
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 del total. ¿Cuánto trasladará el tercero?
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 de lo que queda. ¿Cuánto trasladará el tercero?
Problemas con fracciones.
Problemas con fracciones.
Problemas con fracciones.
Mi padre se ha comido 1/8 de la tableta de turrón y mi madre 2/7 de lo que quedaba. Si costó 4€, ¿cuántos céntimos se comió cada uno?.¿Qué fracción queda?
Problemas resueltos sobre fracciones.
Ejercicios resueltos sobre fracciones.
|
Actividad: Operaciones combinadas con fracciones Efectúa las siguientes operaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Problemas: La fracción como operador 1. El aire es una mezcla de gases. En la capa más próxima a la superficie de la Tierra, se encuentran en las siguientes proporciones:
Solución: Nitrógeno = 750 l.; oxígeno = 200 l.; anhídrido carbónico = 0,3 l.; g. nobles = 49,7 l. 2. La sangre humana se compone de Solución: 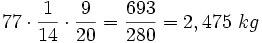 3. Una colonia de verano consta de dos pabellones. En el pabellón A hay 320 personas más que en el B. Sabiendo que en el B se encuentran los Solución: 880 personas; ya que 1/22 del total son 40 personas 4. En un campo se cultivan flores. La cuarta parte son rosas, la sexta parte claveles y el resto son tulipanes. La sexta parte de la parcela dedicada a rosas es para flores blancas. Si el campo tiene 720 m2 y en cada metro cuadrado hay 200 flores, ¿cuántas rosas blancas se recogerán? Solución: 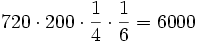 5. En un congreso internacional, Solución: 168 personas ya que 7/24 del total son 49 personas. 6. Disponemos de tres grifos para llenar un depósito. El primero lo llena en 3 horas, el segundo en 4 horas, y el tercero, en 6. Si se abren los tres a la vez, ¿cuánto tardarán en llenar el depósito? Solución: Los tres a la vez llenan los 3/4 del depósito en una hora, luego tardan 1 h. 20 m. 7. La diferencia entre los Solución: 60 8. Si se unen dos cables eléctricos, se obtiene un cable de 440 m. Si sabemos que uno mide los Solución: 160 m. y 280 m. 9. Se siembra un huerto con patatas, puerros y zanahorias. Las patatas ocupan la cuarta parte, los puerros los dos quintos, y las zanahorias, el resto. La parte dedicada a los puerros supera en 30 m2 a la de las zanahorias. ¿Cuál es la extensión del huerto? Solución: 600 m2 ya que 1/20 del huerto mide 30 m2. 10. Por la compra de un apartamento hemos dado como anticipo 24000 € y nos hemos comprometido a pagar 250 € al mes. Después de 24 meses hemos pagado los Solución: 48000 € |
|
Problemas: Fracciones 1. Los Solución: 2. En cierto país trabajan
Solución: 3. De una cantidad de dinero se gasta la tercera parte, después los
Solución: |
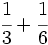 b)
b) 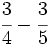
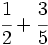
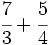
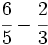

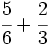 b)
b) 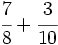 c)
c) 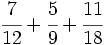
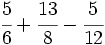
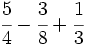
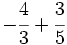

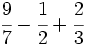
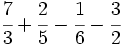
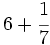
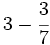
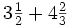
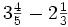
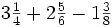
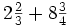
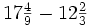
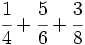
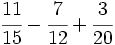
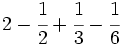
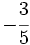 .
.
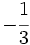 es
es 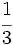 .
.
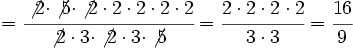
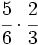
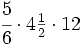
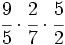
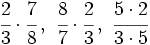
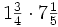
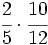
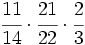
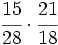
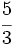 .
.
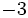 .
.
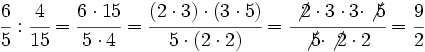
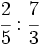
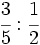
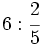
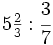
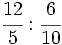
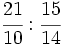
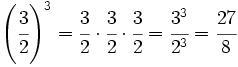
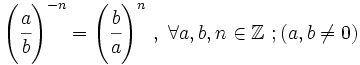
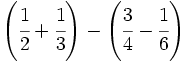 b)
b) 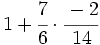 c)
c) 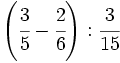
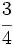 de nitrógeno,
de nitrógeno, 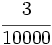 de anhídrido carbónico y el resto son gases nobles.
Halla cuántos litros de cada uno de estos gases se encuentran en 1
de anhídrido carbónico y el resto son gases nobles.
Halla cuántos litros de cada uno de estos gases se encuentran en 1 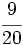 de corpúsculos (glóbulos rojos,glóbulos blancos, plaquetas) y el resto de plasma. Sabiendo que la sangre de una persona constituye aproximadamente
de corpúsculos (glóbulos rojos,glóbulos blancos, plaquetas) y el resto de plasma. Sabiendo que la sangre de una persona constituye aproximadamente 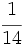 de su masa, ¿cuánto pesan los corpúsculos sanguíneos de un individuo de 77 kg?
de su masa, ¿cuánto pesan los corpúsculos sanguíneos de un individuo de 77 kg?
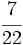 del total, ¿cuántas personas hay en la colonia?
del total, ¿cuántas personas hay en la colonia?
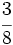 de los asistentes son europeos, y la tercera parte, americanos. Hay 49 asistentes que no son europeos ni americanos. ¿Cuántos congresistas hay?
de los asistentes son europeos, y la tercera parte, americanos. Hay 49 asistentes que no son europeos ni americanos. ¿Cuántos congresistas hay?
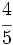 y los
y los 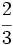 de un número es igual a 8. ¿Cuál es ese número?
de un número es igual a 8. ¿Cuál es ese número?
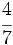 del otro, ¿cuál es la longitud de cada cable?
del otro, ¿cuál es la longitud de cada cable?
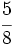 del precio total. Calcula el precio del apartamento.
del precio total. Calcula el precio del apartamento.
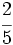 de la población. De los trabajadores,
de la población. De los trabajadores, 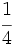 se dedica a la construcción,
se dedica a la construcción, 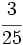 a la industria,
a la industria, 
