Funciones: Dominio e imagen
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:13 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:14 7 ago 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 61: | Línea 61: | ||
| :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | :c) Su dominio es <math>\mathbb{R^+}</math>, porque el radicando no puede ser negativo para poder hallar la raíz. | ||
| }} | }} | ||
| - | |||
| - | ==Puntos de corte con los ejes== | ||
| - | ===Puntos de corte con el eje de ordenadas=== | ||
| - | Para hallar los puntos de corte de la función <math>y=f(x)</math> con el eje Y, basta hacer <math>x=0</math> y averiguar el valor de <math>y</math>. | ||
Revisión de 16:14 7 ago 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Coordenadas | Ejercicios 1 Ejercicios 2 | WIRIS Geogebra Calculadora Función Lista de funciones |
Dominio de definición e imagen
Llamamos dominio de definición de una función y = f(x) al conjunto de valores de la variable independiente x para los cuales existe el valor de y. Lo representaremos por Df .
La imagen o recorrido de una función es el conjunto de valores que toma la variable dependiente y. Lo representaremos por Imf .
 Actividad Interactiva: Dominio e imagen
1. Determina el dominio y la imagen de las siguientes funciones.
Actividad: Observa la escena y mueve el punto P para ver los valores que recorren las variables: a) Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X,¿Cuál es su dominio y su imagen? Observa esta otra escena y procedede como antes: b) ¿Cuál es su dominio y su imagen? Haz lo mismo con esta tercera escena: |
Ejemplo: Dominio de una función
- Halla el dominio de las funciones:
- a)
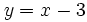b) 
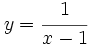c)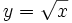 
Solución:
- a) Su dominio es
, porque cualquier valor de x da un valor de y válido.
- b) Su dominio es
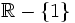, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
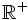, porque el radicando no puede ser negativo para poder hallar la raíz.
