Números naturales: Operaciones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:01 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:56 7 ago 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{Menú Matemáticas 3ESO | ||
| + | |ir= |ampliar= | ||
| + | |repasar= | ||
| + | [http://descartes.cnice.mecd.es/1y2_eso/naturales1/index.htm Operaciones I]<br>[http://descartes.cnice.mecd.es/1y2_eso/naturales2/index.htm Operaciones II]<br>[http://www.gobiernodecanarias.org/educacion/usr/eltanque/Tablas/TablasIE.html Tablas de multiplicar]<br>[http://genmagic.org/moodle/mod/book/view.php?id=157 Mi libreta] | ||
| + | |enlaces=[http://es.wikipedia.org/wiki/Numeros_naturales Números naturales]<br>[http://es.wikipedia.org/wiki/Aritm%C3%A9tica Aritmética] | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Sacar factor común== | ||
| + | La [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales:_Operaciones#Propiedades_de_la_suma_y_el_producto_de_naturales propiedad distributiva] sirve para simplificar expresiones '''sacando factor común'''. Veamos un ejemplo | ||
| + | {{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejemplo: ''Sacar factor común'' | ||
| + | |enunciado= | ||
| + | :Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> | ||
| + | |sol= | ||
| + | El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | ||
| + | <center><math>16xyz-24xz+4x\;\!=</math>{{p}} | ||
| + | <math>(4x) \cdot 4yz - (4x) \cdot 6z + (4x) \cdot 1=\;\!</math>{{p}} | ||
| + | <math>4x \cdot (4yz-6z+1)</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Ejercicios== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios: ''Sacar factor común'' | ||
| + | |cuerpo= | ||
| + | |||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | '''1. '''Extrae factor común: | ||
| + | |||
| + | :a) <math>-18a+20a-10a\,\!</math>{{b}}b) <math>15x-60x^2\,\!</math>{{b}}c) <math>5ba^2-3ab+2ba^3\;\!</math> | ||
| + | <p></p> | ||
| + | |sol= | ||
| + | a) <math>-8a\,\!</math>{{b}}b) <math>15x \cdot (1-4x)\,\!</math>{{b}}c) <math>ab \cdot (5a-3+2a^2)</math> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
Revisión de 19:56 7 ago 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar Mi libreta | WIRIS Geogebra Calculadora Números naturales Aritmética |
Tabla de contenidos |
Operaciones con naturales
Suma y multiplicación de naturales
La suma (o adición) y la multiplicación (o producto) de dos números naturales es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición interna.
Resta y división de naturales
La resta (o substracción)y la división (o cociente) de dos números naturales no siempre es otro número natural. Por eso se dice que estas dos operaciones son leyes de composición externa.
Propiedades de la suma y el producto de naturales
La suma y la multiplicación cumplen las siguientes propiedades:
- Propiedad asociativa:
- Propiedad conmutativa:
- Propiedad distributiva:
Problemas
|
Problemas: Operaciones con naturales
1. Una empresa compra una máquina de café por 6.000 €. Cada mes se gasta 100 € en mantenimiento pero obtiene 350 € por la venta de café. Al cabo de 2 años y medio la vende por 4920 €. ¿Qué beneficio mensual le ha aportado la máquina?
Solución: 214 € |
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Operaciones I Operaciones II Tablas de multiplicar Mi libreta | WIRIS Geogebra Calculadora Números naturales Aritmética |
Sacar factor común
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión
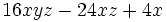
Solución:
El factor común, que se repite en los tres sumandos, es
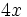 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 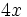 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
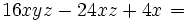
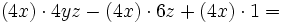
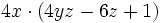
Ejercicios
|
Ejercicios: Sacar factor común 1. Extrae factor común:
Solución: a) 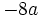 b) b) 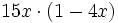 c) c) 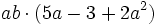 |
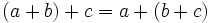
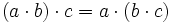
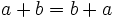
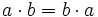
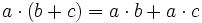
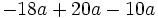 b)
b) 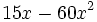 c)
c)