Monomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:58 21 sep 2007 Coordinador (Discusión | contribuciones) (→Monomios) ← Ir a diferencia anterior |
Revisión de 19:08 21 sep 2007 Coordinador (Discusión | contribuciones) (→Monomios) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| ==Monomios== | ==Monomios== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | '''Monomio''' es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas o no a potencias de exponente natural}} | + | *'''Monomio''' es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas o no a potencias de exponente natural. |
| + | *Se llama '''coeficiente''' de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si es un 1 no se escribe y nunca es 0 ya que la expresión completa sería 0. | ||
| + | *Se denomina '''grado''' de un monomio a la suma de los exponentes de las letras. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| - | Son monomios: <math>3ax \, \quad -2xy^2 \, \quad \cfrac{4}{3}\pi r^3</math> | + | :a) <math>3ax \;\!</math> es un monomio de grado 2 y coeficiente 3. |
| + | :b) <math>-2xy^2 \;\!</math> es un monomio de grado 3 y coeficiente -2. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| ===Monomios semejantes=== | ===Monomios semejantes=== | ||
Revisión de 19:08 21 sep 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Monomios
- Monomio es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas o no a potencias de exponente natural.
- Se llama coeficiente de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si es un 1 no se escribe y nunca es 0 ya que la expresión completa sería 0.
- Se denomina grado de un monomio a la suma de los exponentes de las letras.
Ejemplos:
- a)
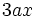 es un monomio de grado 2 y coeficiente 3.
es un monomio de grado 2 y coeficiente 3.
- b)
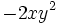 es un monomio de grado 3 y coeficiente -2.
es un monomio de grado 3 y coeficiente -2.

