Números racionales: Expresión decimal de una fracción
De Wikipedia
| Revisión de 07:13 7 nov 2007 Coordinador (Discusión | contribuciones) (→Paso de decimal a fracción) ← Ir a diferencia anterior |
Revisión de 07:44 7 nov 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 19: | Línea 19: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/decimales/decimales1.html | + | url=http://maralboran.org/web_ma/descartes/decimales/decimales1.html |
| width=650 | width=650 | ||
| height=350 | height=350 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/decimales/decimales1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| Línea 31: | Línea 33: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/decimales/decimales3.html | + | url=http://maralboran.org/web_ma/descartes/decimales/decimales3.html |
| width=650 | width=650 | ||
| height=350 | height=350 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/decimales/decimales3.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| Línea 45: | Línea 49: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/decimales/decimales2.html | + | url=http://maralboran.org/web_ma/descartes/decimales/decimales2.html |
| width=720 | width=720 | ||
| height=350 | height=350 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/decimales/decimales2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | |||
| }} | }} | ||
| Línea 81: | Línea 88: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros2_2.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros2_2.html |
| width=650 | width=650 | ||
| height=300 | height=300 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros2_2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
| }} | }} | ||
| Línea 96: | Línea 105: | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_1.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_1.html |
| width=540 | width=540 | ||
| height=210 | height=210 | ||
| name=myframe | name=myframe | ||
| - | </iframe>{{p}} | + | </iframe> |
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | {{p}} | ||
| Pulsa INICIO para ver más ejemplos</center> | Pulsa INICIO para ver más ejemplos</center> | ||
| }} | }} | ||
| Línea 109: | Línea 120: | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_2.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_2.html |
| width=540 | width=540 | ||
| height=210 | height=210 | ||
| name=myframe | name=myframe | ||
| - | </iframe>{{p}} | + | </iframe> |
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | {{p}} | ||
| Pulsa INICIO para ver más ejemplos | Pulsa INICIO para ver más ejemplos | ||
| </center> | </center> | ||
| Línea 123: | Línea 137: | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_3.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_3.html |
| width=540 | width=540 | ||
| height=210 | height=210 | ||
| name=myframe | name=myframe | ||
| - | </iframe>{{p}} | + | </iframe> |
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_3.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| + | {{p}} | ||
| Pulsa INICIO para ver más ejemplos | Pulsa INICIO para ver más ejemplos | ||
| </center> | </center> | ||
| Línea 155: | Línea 171: | ||
| {{p}} | {{p}} | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_4.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_4.html |
| width=690 | width=690 | ||
| height=300 | height=300 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_4.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 07:44 7 nov 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
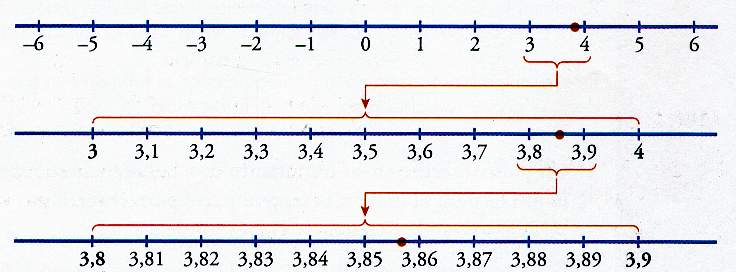
Representación de números decimales
Los números decimales los podemos representar en la recta real de la siguiente manera:
|
Actividad Interactiva: Representación de los números decimales
Actividad 1. Representación de números decimales con una cifra decimal.
Actividad: Selecciona un número entre -10 y 10 o bien entre -200 y 200 pulsando en el botón correspondiente. Si el número no se encuentra en la pantalla, mueve el eje hasta encontrarlo y posteriormente arrastra la bola hasta la posición buscada.
Actividad 2. Decimal comprendido entre dos.
Actividad: Debes de colocar un número decimal comprendido entre los dos decimales que ofrece la pantalla.
Actividad 3. Representación de números decimales con dos o tres cifras decimales.
Actividad: Selecciona una de las dos opciones, o un número decimal con dos cifras decimales o un decimal con tres cifras decimales pulsando en el botón correspondiente. Si el número no se encuentra en la pantalla, mueve el eje hasta encontrarlo y posteriormente arrastra la bola hasta la posición buscada. |
Paso de fracción a decimal
Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:- Expresión decimal exacta: Si tiene un número finito de decimales.
- Por ejemplo:
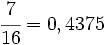 .
.
- Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.
- Por ejemplo:
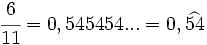 . El periodo es 54.
. El periodo es 54.
- Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.
- Por ejemplo:
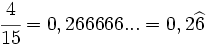 . El periodo es 6 y el anteperiodo 2.
. El periodo es 6 y el anteperiodo 2.
Identificar el tipo de expresión decimal sin hacer la división
Se puede saber, sin hacer la división, que tipo de expresión decimal tiene una fracción. Para ello, deberemos simplificar la fracción y nos fijaremos en la descomposición del denominador en factores primos. Tendremos los siguientes casos:
- Si el denominador sólo contiene factores que sean 2 ó 5, la fracción tiene una expresión decimal exacta.
- Si el denominador no contiene factores que sean 2 ó 5, la fracción tiene una expresión decimal periódica pura.
- Si el denominador contiene mezcla de factores que sean 2 ó 5, con otros distintos de 2 ó 5, la fracción tiene una expresión decimal periódica mixta.
|
Actividad Interactiva: Expresión decimal de una fracción
Actividad 1. Averigua el tipo de expresión decimal de una fracción y hállala posteriormente
Actividad: Pulsa el botón "EJERCICIO" para generar una fracción. Debes averiguar de que tipo de expresión decimal se trata sin hacer la división. Luego halla su expresión decimal. Lo haces en tu cuaderno, escribe la solución en la casilla "Expresión Decimal" y pulsa el botón "SOLUCIÓN" para ver si lo has hecho bien. |
Paso de decimal a fracción
Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:
Decimales exactos: Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
Decimales periódicos puros: La fracción de un número decimal periódico puro tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo.
Decimales periódicos mixtos: Tendrá como numerador la diferencia entre a y b, donde a es el número escrito sin la coma, y b es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
Veamos unos ejemplos que ilustren el porqué de tales procedimientos:
Ejemplo: Paso de decimal a fracción
- Expresa en forma de fracción los números decimales:
- a)
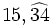 b)
b) 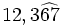
- a)
- a)
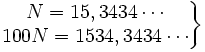 Restando:
Restando: 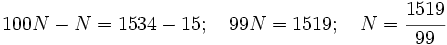
- b)
 Restando:
Restando: 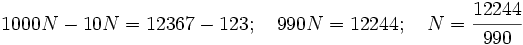
|
Actividad Interactiva: Paso de decimal a fracción
Actividad 1. Averigua la fracción que corresponde con la expresión decimal.
Actividad: Pulsa el botón "EJERCICIO" para generar una expresión decimal. Debes buscar la fracción generatriz. No olvides simplificarla. Lo haces en tu cuaderno, escribes el numerador de la solución en el control numerador y el denominador de la solución en el control denominador y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien. |
|
Calculadora: Fracciones. Paso a decimal y viceversa |
Ejercicios
|
Ejercicios: 8. Sin hacer la división, indica qué tipo de decimal resulta:
Solución: a) Decimal exacto; b) Decimal periódico puro; c) Decimal periódico mixto. 8. Expresa en forma de fracción:
Solución: a) 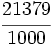 b) b) 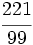 c) c) 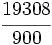 |
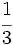
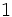

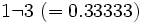
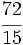 b)
b) 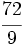 c)
c)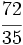
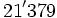 b)
b) 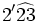 c)
c)