Números irracionales
De Wikipedia
| Revisión de 23:54 8 nov 2007 Juanmf (Discusión | contribuciones) (→Representación de números irracionales) ← Ir a diferencia anterior |
Revisión de 17:20 10 nov 2007 Juanmf (Discusión | contribuciones) (→Números irracionales) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| {{Caja_Amarilla|texto=A los números cuya expresión decimal tiene infinitas cifras no periódicas, se les llama números '''irracionales.''' Al conjunto de tales números lo representaremos con la letra <math>\mathbb{I}</math>.}} | {{Caja_Amarilla|texto=A los números cuya expresión decimal tiene infinitas cifras no periódicas, se les llama números '''irracionales.''' Al conjunto de tales números lo representaremos con la letra <math>\mathbb{I}</math>.}} | ||
| {{p}} | {{p}} | ||
| - | Son números irracionales: <math>\pi=3.141592654..., \sqrt{2}=1.414213..., e=2.718281...</math>{{p}} | + | Son números irracionales: <math>\pi=3.141592654..., \sqrt{2}=1.414213..., e=2.718281...\varphi = \frac{1 + \sqrt{5}}{2} \approx 1,618033988\,749\,894\,848\,204\, |
| + | 586\,834\,365\,638\,117\,720\,309\,179\,805\, ...</math>{{p}} | ||
| Vamos a repasar los distintos conjuntos numéricos vistos hasta ahora: | Vamos a repasar los distintos conjuntos numéricos vistos hasta ahora: | ||
| {{p}} | {{p}} | ||
Revisión de 17:20 10 nov 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Potencias y Raíces | WIRIS Geogebra Calculadora Raíz cuadrada |
Números irracionales
A los números cuya expresión decimal tiene infinitas cifras no periódicas, se les llama números irracionales. Al conjunto de tales números lo representaremos con la letra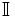 
.
Vamos a repasar los distintos conjuntos numéricos vistos hasta ahora:
 Actividad Interactiva: Números irracionales
Actividad 1. Conjuntos numéricos.
Actividad: Pulsa los botones para ver ejemplos de los distintos tipos de números. |
Proposición
- El número
es irracional.
Vamos ha utilizar un tipo de demostración denominado "por reducción al absurdo". Vamos a suponer que es racional y llegaremosa una conclusión sin sentido. Esto demostraría que no puede ser racional sino irracional.
Por tanto, supongamos que es racional, o sea, que existe una fracción de números enteros 
que es igual a . Dicha fracción la podemos suponer irreducible, ya que siempre es posible sinplificarla.
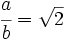
Elevamos al cuadrado los dos miembros de la igualdad:
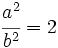
Multiplicamos por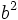 
los dos miembros de la igualdad:
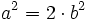
Esta expresión nos dice que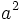 
es par, ya que resulta de multiplicar 2 por otro número.
Pero 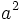es un cuadrado perfecto, o sea es un número entero al cuadrado, luego si uno de sus factores es el 2, el 2 tiene que estar como mínimo al cuadrado, o sea dos veces.
Por tanto como ya hay un 2 en la igualdad delante de 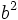, el otro 2 tiene que estar en el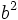
Eso quiere decir que 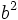también tiene que ser par, y por tanto 
también es par.
Pero si 
es par y también, la fracción no es irreducible, como habíamos supuesto.
Representación de números irracionales
En la siguiente actividad vamos a ver algunos números irracionales importantes y su representación en la recta real.
Actividades Interactivas: Representación de números irracionales
1. Representación del número
.Actividad: Observa en la escena la representación de .
2. Representación del número de oro Actividad: Desde la antigüedad matemáticos filósofos y artistas han creído en la existencia de una razón privilegiada, que fue llamada número áureo. Los griegos consideraban que un rectángulo cuyos lados Es el primer número irracional del que se tuvo conciencia de que lo era. En la escena puedes ver la representación del número de oro
3. Representación de otras raíces cuadradas.
Actividad: Observa en la escena la representación de otras raices cuadradas.
|
.
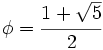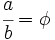es especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte.
vídeo: La divina proporción
