Ángulos en la circunferencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 22:23 18 dic 2007 Coordinador (Discusión | contribuciones) (→Ángulo inscrito) ← Ir a diferencia anterior |
Revisión de 22:29 18 dic 2007 Coordinador (Discusión | contribuciones) (→Ángulo inscrito) Ir a siguiente diferencia → |
||
| Línea 28: | Línea 28: | ||
| {{p}} | {{p}} | ||
| {{Teorema | {{Teorema | ||
| - | |titulo=Propiedades: ''Ángulo incrito'' | + | |titulo=Propiedades: ''Ángulo inscrito'' |
| |enunciado= | |enunciado= | ||
| - | :a) Los ángulos inscritos que abarcan el mismo arco son iguales. | + | :a) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente. |
| - | :b) La medida del ángulo inscrito es la mitad del ángulo central correspondiente. | + | :b) Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales. |
| + | |||
| |demo= | |demo= | ||
| <center><iframe> | <center><iframe> | ||
| Línea 40: | Línea 41: | ||
| </iframe></center> | </iframe></center> | ||
| - | :a) Mueve el vértice V y observa que no varía la medida del ángulo AVB. | + | :a) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. |
| - | :b) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde. | + | :b) Mueve el vértice V y observa que no varía la medida del ángulo AVB. |
| + | |||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 22:29 18 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ángulos (1ºESO) | WIRIS Geogebra Calculadora |
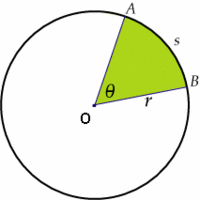
Ángulo central
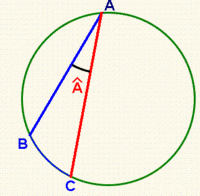
Ángulo inscrito
Propiedades: Ángulo inscrito
- a) La medida de un ángulo inscrito en una circunferencia es la mitad del arco que abarca, es decir, la mitad del ángulo central correspondiente.
- b) Como consecuencia, dos ángulos inscritos en una circunferencia, que abarcan el mismo arco son iguales.
Demostración:
- a) Mueve los puntos A y B y comprueba que el ángulo inscrito mide la mitad que el arco central que le corresponde.
- b) Mueve el vértice V y observa que no varía la medida del ángulo AVB.
 y su arco correspondiente AB.
y su arco correspondiente AB.
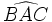 .
.