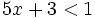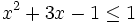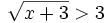Plantilla:Inecuaciones con una incógnita
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:23 18 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:28 19 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| *<math>\sqrt{x+3}>3\;</math> | *<math>\sqrt{x+3}>3\;</math> | ||
| }} | }} | ||
| + | {{p}} | ||
| + | ===Transformaciones que mantienen la equivalencia de las inecuaciones=== | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | *Sumar o restar la misma expresión en los dos miembros de la desigualdad. (Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.) | ||
| + | *Multiplicar o dividir los dos miembros de la desigualdad por un mismo número mayor que cero. (Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.) | ||
| + | *Al multiplicar o dividir por un número negativo los dos miembros de la desigualdad, ésta cambia de sentido, es decir, pasa de ser (<math>>\;</math> ó <math>\ge</math>) a (<math><\;</math> ó <math>\le</math>), o viceversa. | ||
| + | }} | ||
| + | {{p}} | ||
Revisión de 19:28 19 ene 2009
- Una inecuación con una incógnita es una desigualdad entre expresiones algebraicas con una sola variable. Para las desigualdades utilizaremos los símbolos:
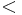 (menor que);
(menor que);  (mayor que);
(mayor que); 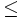 (menor o igual que) y
(menor o igual que) y 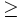 (mayor o igual que).
(mayor o igual que).
- Una solución de una inecuación con una incógnita,
 , es un valor de la variable
, es un valor de la variable  que hace que se cumpla la desigualdad.
que hace que se cumpla la desigualdad.
- Resolver una inecuación consiste en hallar todas sus soluciones. Habitualmente son infinitas y se expresan mediante intervalos de la recta real, aunque tambien puede ser finitas o no existir.
Ejemplos:
Son inecuaciones con una incógnita:
Transformaciones que mantienen la equivalencia de las inecuaciones
- Sumar o restar la misma expresión en los dos miembros de la desigualdad. (Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa.)
- Multiplicar o dividir los dos miembros de la desigualdad por un mismo número mayor que cero. (Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa.)
- Al multiplicar o dividir por un número negativo los dos miembros de la desigualdad, ésta cambia de sentido, es decir, pasa de ser (
 ó
ó 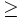 ) a (
) a (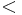 ó
ó 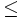 ), o viceversa.
), o viceversa.