Triángulos
De Wikipedia
| Revisión de 06:58 28 abr 2009 Coordinador (Discusión | contribuciones) (→Rectas y puntos notables en un triángulo) ← Ir a diferencia anterior |
Revisión de 07:00 28 abr 2009 Coordinador (Discusión | contribuciones) (→Rectas y puntos notables en un triángulo) Ir a siguiente diferencia → |
||
| Línea 235: | Línea 235: | ||
| El baricentro, suele denotarse por la letra G, Centro de '''G'''ravedad. | El baricentro, suele denotarse por la letra G, Centro de '''G'''ravedad. | ||
| - | Como se ve en la figura, el segmento CG es de medida el doble que el segmento GD. | + | Como se ve en la figura, el segmento CG mide el doble que el segmento GD. |
| - | Realiza en tu cuaderno los siguientes ejercicios: | + | *¿Es posible determinar el baricentro trazando solamente una mediana? Explica el procedimiento. |
| - | + | ||
| - | # Mueve los vértices del triángulo hasta conseguir que GD=1,80 cm. En esa situación ¿Cuánto mide la mediana CD? | + | |
| - | # ¿Es posible determinar el baricentro trazando solamente una mediana? Explica el procedimiento. | + | |
| }} | }} | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
Revisión de 07:00 28 abr 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Triángulos | WIRIS Geogebra Calculadora Triángulo |
Tabla de contenidos |
Triángulo
Propiedades
- Todo triángulo cumple las siguientes propiedades:
- Sus tres ángulos suman 180º.
- La longitud de cada lado es menor que la suma de los otros dos.
- Es rígido, de hecho, es el único polígono indeformable.
1. Los tres ángulos de un triángulo suman 180º.
Para comprobar esta propiedad vamos a hacer uso de la siguiente escena. En ella, A es un punto fijo, B puede moverse horizontalmente y C libremente: esto permite dibujar cualquier triángulo. La recta que pasa por C es paralela al lado AB con lo cual los ángulos verdes son iguales y los amarillos también (alternos internos). Si sumamos los tres ángulos en el vértice C, obtenemos siempre un ángulo llano.
2. La longitud de cada lado es menor que la suma de los otros dos.
En la siguiente escena puedes comprobar esta propiedad. Mueve los vértices para cambiar la forma del triángulo.
3. Es rígido, de hecho, el triángulo es el único polígono indeformable.
Observa la escena, arrastra los vértices y comprueba que:
a) Con tres varillas iguales podemos formar un triángulo, que no se deforma.
b) Con cuatro varillas iguales, el cuadrilátero que se forma, puede deformarse, no es rígido.
Esta propiedad tiene muchas aplicaciones en la construcción. Observa torres de la luz, estructuras metálicas de puentes,... la forma externa puede ser variada, pero llevan diagonales internas que dividen su estructura en triángulos.Clasificación de los triángulos
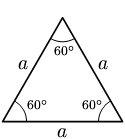
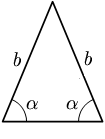
Según sus lados
|
|
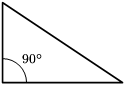
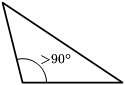
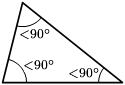
Según sus ángulos
|
|
|
Actividad Interactiva: Clasificación de los triángulos
Actividad 1: En la siguiente escena podrás manipular un triángulo y ver como son sus lados y sus ángulos.
Actividad: Contesta en tu cuaderno: a) Si un triángulo tiene dos ángulos agudos, ¿también lo es el tercero? En la siguiente escena, mueve los vértices para cambiar el valor de los ángulos y comprueba los resultados que has obtenido. |
Construcción de triángulos
Un triángulo, tiene tres lados y tres ángulos. Para construir un triángulo hay que conocer tres de esos datos, siendo al menos uno de ellos un lado:
- Conocidos los tres lados.
- Conocidos dos lados y el ángulo comprendido entre ellos.
- Conocido un lado y sus dos ángulos contiguos.
|
Actividad Interactiva: Construcción de triángulos
1. Construcción de un triángulo conociendo los tres lados.
Actividad: El proceso de construcción se muestra en la figura: Recuerda que para poder realizar la construcción la medida de cada lado ha de ser menor que la suma de los otros dos.
2. Construcción de un triángulo, conocidos dos lados y el ángulo comprendido entre ellos.
Actividad: El proceso de construcción se muestra en la figura:
3. Construcción de un triángulo conocido un lado y sus dos ángulos contiguos.
Actividad: El proceso de construcción se muestra en la figura: La suma de los dos ángulos conocidos ha de ser menor de 180º.
|
Igualdad de triángulos
Dos triángulo son iguales si tienen sus lados y sus ángulos iguales.
Para que dos triángulos sean iguales basta con que se verifique una de las siguientes condiciones:
- Dos triángulos son iguales si tienen los tres lados iguales.
- Dos triángulos son iguales si tienen dos lados iguales y también es igual el ángulo comprendido entre ellos.
- Dos triángulos son iguales si tienen un lado igual y son iguales sus ángulos contiguos.
Rectas y puntos notables en un triángulo
- Medianas y baricentro
La mediana de un triángulo es una recta que une cada vértice con el punto medio del lado opuesto. Las tres medianas se cortan en un punto llamado baricentro y es el centro de gravedad del triángulo: desde este punto podríamos atarlo con un hilo y quedaría suspendido horizontalmente.
- Alturas y ortocentro
La altura de un triángulo es la perpendicular desde un vértice al lado opuesto. Las tres alturas de un triángulo se cortan en un punto llamado ortocentro.
- Mediatrices y circuncentro
Las mediatrices de un triángulo son las perpendiculares a los puntos medios de cada lado. Las tres mediatrices siempre se cortan en un punto llamado circuncentro, que es el centro de la circunferencia circunscrita (la que pasa por los tres vértices del triángulo).
- Bisectrices e incentro
Las tres bisectrices de un triángulo cualquiera se cortan en un punto llamado incentro, que es el centro de la circunferencia inscrita al triángulo. La circunferencia inscrita es una circunferencia tangente a los tres lados del triángulo.
|
Actividad Interactiva: Elementos notables de un triángulo
1. Medianas y baricentro.
Actividad: Se llama mediana de un triángulo al segmento que une un vértice con el punto medio del lado opuesto. Las tres medianas de un triángulo se cortan en un punto que se llama baricentro. El baricentro, G, siempre está en el interior del triángulo. Mueve los vértices del triángulo y comprueba que siempre es así. El baricentro, suele denotarse por la letra G, Centro de Gravedad. Como se ve en la figura, el segmento CG mide el doble que el segmento GD.
2. Alturas y ortocentro.
Actividad: Altura de un triángulo es el segmento que une un vértice con el lado opuesto o su prolongación formando ángulo recto. Las tres alturas de un triángulo, o sus prolongaciones, se cortan en un punto que se llama ortocentro. Contesta en tu cuaderno:
3. Mediatrices y circuncentro.
Actividad: Recuerda que la mediatriz de un segmento, es la recta perpendicular al segmento en su punto medio. Observa que las tres mediatrices se cortan en un punto, que se denomina circuncentro (Ci). Mueve los vértices del triángulo y comprueba que siempre es así.
A esta circunferencia se le llama circunferencia circunscrita. Mueve los vértices del triángulo para comprobar que el circuncentro es el centro de la circunferencia circunscrita. Para determinar el circuncentro, basta con trazar dos de las mediatrices y su punto de corte. Ya sabemos que la tercera mediatriz también se corta con las anteriores en el mismo punto. El trazado de mediatrices, y en consecuencia el circuncentro resuelven dos importantes problemas geométricos
Ejercicios:
4. Recta de Euler.
Actividad: En la figura se muestran el ortocentro, baricentro y circuncentro. Mueve los vértices del triángulo y observa que estos tres puntos están siempre alineados, (pertenecientes a la misma recta). Mueve el botón situado fuera del triángulo y observa la relación que existe entre las distancias entre ellos. A la recta que contiene a estos tres puntos, se la denomina recta de Euler, en honor a su descubridor.
5. Bisectrices e incentro.
Actividad: La bisectriz de un ángulo es la semirrecta que lo divide en dos ángulos iguales. Las tres bisectrices de los ángulos un triángulo se cortan en un punto que se llama incentro. El incentro siempre es un punto situado en el interior del triángulo. El incentro tiene una importante propiedad, y de ahí su nombre, es el centro de la circunferencia inscrita en el triángulo.
La circunferencia inscrita es tangente los tres lados, por tanto, el incentro equidista de los tres lados del triángulo. Observa la siguiente escena y contesta en tu cuaderno: El incentro, para un triángulo cualquiera, no está alineado con el ortocentro, baricentro y circuncentro, pero si lo está en un tipo de triángulo. Mueve los vértices del triángulo de forma que el incentro esté en la recta que pasa por ortocentro, circuncentro y baricentro. ¿Cómo es el triángulo en este caso? Mueve nuevamente los vértices del triángulo hasta conseguir que sea equilátero (aproximadamente). ¿Qué ocurre?
6. Identifica los puntos notables de un triángulo.
Actividad: Observa la siguiente escena y contesta en tu cuaderno quién es cada punto: Debes mover los vértices del triángulo hasta conseguir saber cual es cada uno. Explica el razonamiento que has seguido para saber cual es cada punto. |
Triángulos rectángulos
Un triángulo rectángulo es el que tiene un ángulo recto. El mayor de los lados, opuesto al ángulo recto, se le llama hipotenusa. A los otros dos, que forman el ángulo recto, se les llama catetos. | 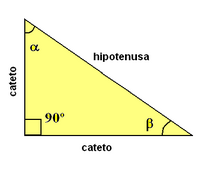
|
|
Actividad Interactiva: Triángulo rectángulo
1. Construcción de un triángulo rectángulo usando una circunferencia.
Actividad: La siguiente escena muestra como construir un triángulo rectángulo. Consiste en inscribirlo en una circunferencia cuyo diámetro cincida con la hipotenusa. Mueve el punto C y comprueba que el triángulo inscrito de esta forma siempre es rectángulo. |
Ejercicios
Ejercicios de autoevaluación
|
Ejercicios de autoevaluación |
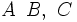 .
.
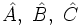 , aunque también son usuales las letras griegas:
, aunque también son usuales las letras griegas: 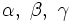 .
.
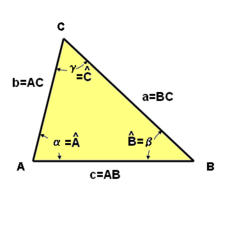
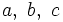 ; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas:
; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: 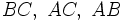 , las de los vértices contenidos en ese lado.
, las de los vértices contenidos en ese lado.