Números racionales: Operaciones
De Wikipedia
| Revisión de 18:11 26 oct 2009 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 18:14 26 oct 2009 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 272: | Línea 272: | ||
| :b) <math>1+\cfrac{7}{6} \cdot \cfrac{-2}{14} </math> | :b) <math>1+\cfrac{7}{6} \cdot \cfrac{-2}{14} </math> | ||
| :c) <math>\left ( \cfrac{3}{5}-\cfrac{2}{6} \right ):\cfrac{3}{15}</math> | :c) <math>\left ( \cfrac{3}{5}-\cfrac{2}{6} \right ):\cfrac{3}{15}</math> | ||
| - | :d) <math>\cfrac{1}{2}-\cfrac{5}{6}:\cfrac{10}{2}+\cfrac{5}{12}: \left ( \cfrac{5}{4} \right ) ^{-1}</math> | + | :d) <math>\cfrac{1}{2}-\cfrac{5}{6}:\cfrac{10}{2}+\cfrac{5}{12}: \left ( \cfrac{5}{4} +1\right )</math> |
| :e) <math>\cfrac{\cfrac {1}{3}-\left ( \cfrac{3}{4}-\cfrac{2}{6}+1 \right )}{2+\cfrac {2}{3}}</math> | :e) <math>\cfrac{\cfrac {1}{3}-\left ( \cfrac{3}{4}-\cfrac{2}{6}+1 \right )}{2+\cfrac {2}{3}}</math> | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>\frac{1}{4}</math>{{b4}}b) <math>\frac{5}{6}</math>{{b4}}c)<math>\frac{4}{3}</math>{{b4}}d) <math>\frac{41}{48}</math> | + | a) <math>\frac{1}{4}</math>{{b4}}b) <math>\frac{5}{6}</math>{{b4}}c)<math>\frac{4}{3}</math>{{b4}}d) <math>\frac{14}{27}</math> |
| {{b4}}e) <math>-\frac{13}{32}</math> | {{b4}}e) <math>-\frac{13}{32}</math> | ||
Revisión de 18:14 26 oct 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Fracciones IV | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
Operaciones con fracciones
Suma y resta de fracciones
Para sumar o restar fracciones:
- Si las fracciones tienen el mismo denominador, se suman o restan los numeradores y se pone el mismo denominador.
- Si tienen distintos denominadores, primero se reducen a común denominador y luego se procede como en el caso anterior.
Ejemplo: Suma y resta de fracciones
- Calcula:
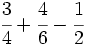
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
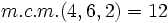 .
.
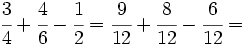
Luego sumamos o restamos los númeradores, dejando el mismo denominador:
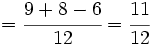
|
Actividad Interactiva: ''Suma y resta de fracciones
Actividad 1: Aprende a sumar y restar fracciones.
Actividad: Cuando tenemos juntas sumas y restas seguimos el mismo proceso que si tuviéramos solamente sumas. Para sumar y restar fracciones es necesario que tengan todas el mismo denominador. Si las fracciones tienen distintos denominadores se pasan a común denominador, es decir, se cambian por otras equivalentes a ellas pero con el mismo denominador todas. Para ello se siguen estos pasos:
En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Realiza las siguientes sumas y restas de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
|
Ejercicios: Suma y resta de fracciones 1. Efectúa las siguientes operaciones:
Solución: a) 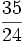 b) b)  c) c) 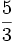 |
Multiplicación de fracciones
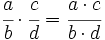
Ejemplo: Producto de fracciones
- Calcula:
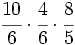
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto:
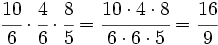
|
Actividad Interactiva: ''Producto de fracciones
Actividad 1: Aprende a multiplicar fracciones.
Actividad: Para multiplicar fracciones no hace falta pasarlas a común denominador, se multiplican directamente. Multiplicamos sus numeradores y lo ponemos de numerador, multiplicamos sus denominadores y lo ponemos de denominador. A continuación se simplifican. No obstante, es conveniente simplificar antes de multiplicar. En esta escena puedes ver el proceso paso a paso, pulsando sobre el triángulo azul. Pulsa "inicio" para que aparezcan otras fracciones.
Actividad 2: Realiza las siguientes multiplicaciones de fracciones.
Actividad: Realiza en papel aparte estas operaciones y luego marca aquí su resultado. Marca primero su numerador, pulsa intro, luego marca su denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no permite rectificaciones, por eso no emplees los triángulos para variar el número marcado. Pulsa "inicio" para que aparezcan otras fracciones. |
|
Ejercicios: Multiplicación de fracciones 1. Efectúa las siguientes operaciones:
Solución: a) 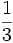 b) b) 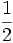 c) c) 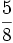 |
Inversa de una fracción
Dada una fracción 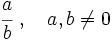 , su inversa es la fracción
, su inversa es la fracción 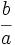 .
.
Por ejemplo, la inversa de 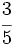 es
es 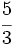 .
.
|
Actividad Interactiva: Inversa de una fracción
Actividad 1: Halla la fracción inversa de una fracción.
Actividad: La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa. Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados. Pulsa "inicio" para que aparezca otra fracción. |
División de fracciones
Para dividir dos fracciones, se pone como numerador, el producro del primer numerador por el segundo denominador, y como denominador, el producto del primer denominador por el segundo numerador.
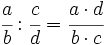
Ejemplo: Cociente de fracciones
- Calcula:
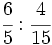
Multiplicamos en cruz, simplificando antes de efectuar el producto:
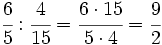
|
Actividad Interactiva: Cociente de fracciones
Actividad 1: Aprende a dividir fracciones.
Actividad: Dividir una fracción por otra es lo mismo que multiplicar la primera fracción por la inversa de la segunda fracción. Una fracción se puede dividir por cualquier otra, menos por la fracción 0. Haz la división en tu cuaderno y luego comprueba el resultado, viendo el desarrollo paso a paso. Para ello pulsa la flecha azul. Pulsa "inicio" para que aparezca otra fracción. |
|
Ejercicios: División de fracciones 1. Efectúa las siguientes operaciones:
Solución: a) 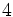 b) b) 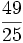 |
La fracción como operador
Para calcular una fracción  de una cantidad
de una cantidad 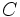 , procederemos multiplicando la fracción por la cantidad
, procederemos multiplicando la fracción por la cantidad 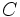 :
:
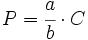
Ejemplo: La fracción como operador
- De una herencia de 27 millones de euros, María recibe las tres quintas partes, su hermano Ramón, la mitad del resto, y su hermana Matilde, lo que queda.
- a) ¿Qué fracción le corresponde a cada uno?
- b) Calcula cuánto se lleva cada uno.
a) Calculamos la fracción que se cada uno:
- María recibe:
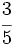
- Ramón recibe:
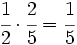
- Matilde recibe:
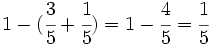
b) Calculamos cuántos euros se lleva cada uno:
- María recibe:
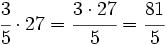 millones de €
millones de €
- Ramón recibe:
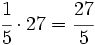 millones de €
millones de €
- Matilde recibe:
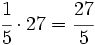 millones de €
millones de €
Ejercicios
|
Ejercicios: Operaciones combinadas con fracciones 1. Efectúa las siguientes operaciones:
Solución: a) 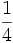 b) b) 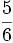 c) c)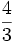 d) d) 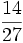 e)
e) 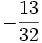 |
|
Problemas: La fracción como operador 1. El aire es una mezcla de gases. En la capa más próxima a la superficie de la Tierra, se encuentran en las siguientes proporciones:
Solución: Nitrógeno = 750 l.; oxígeno = 200 l.; anhídrido carbónico = 0,3 l.; g. nobles = 49,7 l. 2. La sangre humana se compone de Solución: 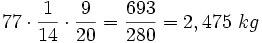 3. Una colonia de verano consta de dos pabellones. En el pabellón A hay 320 personas más que en el B. Sabiendo que en el B se encuentran los Solución: 880 personas; ya que 1/22 del total son 40 personas 4. En un campo se cultivan flores. La cuarta parte son rosas, la sexta parte claveles y el resto son tulipanes. La sexta parte de la parcela dedicada a rosas es para flores blancas. Si el campo tiene 720 m2 y en cada metro cuadrado hay 200 flores, ¿cuántas rosas blancas se recogerán? Solución: 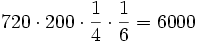 5. En un congreso internacional, Solución: 168 personas ya que 7/24 del total son 49 personas. 6. Disponemos de tres grifos para llenar un depósito. El primero lo llena en 3 horas, el segundo en 4 horas, y el tercero, en 6. Si se abren los tres a la vez, ¿cuánto tardarán en llenar el depósito? Solución: Los tres a la vez llenan los 3/4 del depósito en una hora, luego tardan 1 h. 20 m. 7. La diferencia entre los Solución: 60 8. Si se unen dos cables eléctricos, se obtiene un cable de 440 m. Si sabemos que uno mide los Solución: 160 m. y 280 m. 9. Se siembra un huerto con patatas, puerros y zanahorias. Las patatas ocupan la cuarta parte, los puerros los dos quintos, y las zanahorias, el resto. La parte dedicada a los puerros supera en 30 m2 a la de las zanahorias. ¿Cuál es la extensión del huerto? Solución: 600 m2 ya que 1/20 del huerto mide 30 m2. 10. Por la compra de un apartamento hemos dado como anticipo 24000 € y nos hemos comprometido a pagar 250 € al mes. Después de 24 meses hemos pagado los Solución: 48000 € |
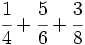 b)
b) 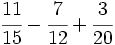 c)
c) 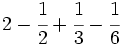
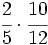 b)
b) 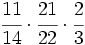 c)
c) 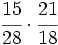
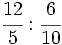 b)
b) 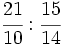
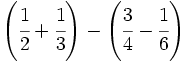
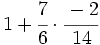
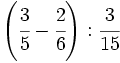
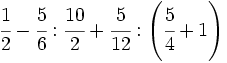
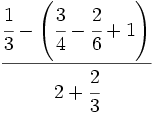
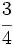 de nitrógeno,
de nitrógeno, 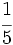 de oxígeno,
de oxígeno, 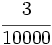 de anhídrido carbónico y el resto son gases nobles.
Halla cuántos litros de cada uno de estos gases se encuentran en 1
de anhídrido carbónico y el resto son gases nobles.
Halla cuántos litros de cada uno de estos gases se encuentran en 1 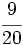 de corpúsculos (glóbulos rojos,glóbulos blancos, plaquetas) y el resto de plasma. Sabiendo que la sangre de una persona constituye aproximadamente
de corpúsculos (glóbulos rojos,glóbulos blancos, plaquetas) y el resto de plasma. Sabiendo que la sangre de una persona constituye aproximadamente 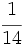 de su masa, ¿cuánto pesan los corpúsculos sanguíneos de un individuo de 77 kg?
de su masa, ¿cuánto pesan los corpúsculos sanguíneos de un individuo de 77 kg?
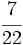 del total, ¿cuántas personas hay en la colonia?
del total, ¿cuántas personas hay en la colonia?
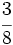 de los asistentes son europeos, y la tercera parte, americanos. Hay 49 asistentes que no son europeos ni americanos. ¿Cuántos congresistas hay?
de los asistentes son europeos, y la tercera parte, americanos. Hay 49 asistentes que no son europeos ni americanos. ¿Cuántos congresistas hay?
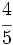 y los
y los 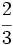 de un número es igual a 8. ¿Cuál es ese número?
de un número es igual a 8. ¿Cuál es ese número?
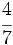 del otro, ¿cuál es la longitud de cada cable?
del otro, ¿cuál es la longitud de cada cable?
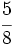 del precio total. Calcula el precio del apartamento.
del precio total. Calcula el precio del apartamento.

