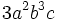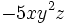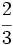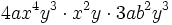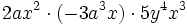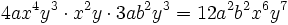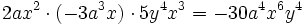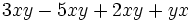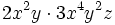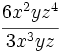Monomios
De Wikipedia
| Revisión de 17:59 6 oct 2014 Coordinador (Discusión | contribuciones) (→Monomios semejantes) ← Ir a diferencia anterior |
Revisión de 18:42 6 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 42: | Línea 42: | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :a) degree 3a^2b^3c | + | :a) {{consulta|texto=degree 3a^2b^3c´}} |
| - | :b) degree -5xy^2z | + | :b) {{consulta|texto=degree -5xy^2z}} |
| - | :b) degree 2/3 | + | :b) {{consulta|texto=degree 2/3}} |
| <center><iframe> | <center><iframe> | ||
| Línea 117: | Línea 117: | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :a) 3xy-5xy+2xy+yx | + | :a) {{consulta|texto=3xy-5xy+2xy+yx}} |
| - | :b) (2x^2*y) * (3x^4*y^2*z) | + | :b) {{consulta|texto=(2x^2*y) * (3x^4*y^2*z)}} |
| - | :b) (6x^2*y*z^4) / (3x^3*y*z) | + | :b) {{consulta|texto=(6x^2*y*z^4) / (3x^3*y*z)}} |
| <center><iframe> | <center><iframe> | ||
Revisión de 18:42 6 oct 2014
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Algebra (1º ESO) | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Monomios
- Monomio es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas a potencias de exponente natural.
- Se llama coeficiente de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si es un 1 no se escribe y nunca es 0 ya que la expresión completa sería 0.
- Se denomina grado de un monomio a la suma de los exponentes de las letras.
- a)
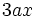 es un monomio de grado 2 y coeficiente 3.
es un monomio de grado 2 y coeficiente 3.
- b)
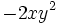 es un monomio de grado 3 y coeficiente -2.
es un monomio de grado 3 y coeficiente -2.
- c)
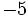 es un monomio de grado 0 y coeficiente -5.
es un monomio de grado 0 y coeficiente -5.
Monomios semejantes
Son monomios semejantes aquellos en los que aparecen las mismas letras con los mismos exponentes.
Son monomios semejantes:
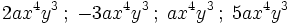
|
Actividad: Grado de un monomio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Operaciones con monomios
Suma y resta de monomios
Para sumar o restar dos monomios tienen que ser semejantes. La suma o resta es otro monomio semejante a ellos que tiene por coeficiente la suma o diferencia, según el caso, de los coeficientes.
Ejemplos: Suma y resta de monomios
- Calcula:
- a)
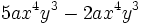
- b)
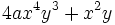
- a)
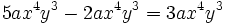
- b)
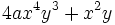 no se pueden sumar por no ser semejantes.
no se pueden sumar por no ser semejantes.
Producto de monomios
Recordemos que para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes
Así, para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican.
División de monomios
Entenderemos la división como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Ejemplos: División de monomios
- Calcula:
- a)
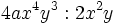
- b)
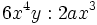
- a)
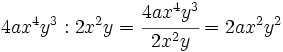
- b)
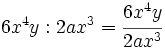 . No es posible la división pues no hay
. No es posible la división pues no hay  en el numerador.
en el numerador.
|
Actividad: Operaciones con monomios
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|