Progresiones geométricas (3ºESO Académicas)
De Wikipedia
| Revisión de 15:39 14 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:48 14 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| {{Ejemplo|titulo=Ejercicio resuelto: ''Progresión geométrica'' | {{Ejemplo|titulo=Ejercicio resuelto: ''Progresión geométrica'' | ||
| |enunciado={{p}} | |enunciado={{p}} | ||
| - | :En una progresión geométrica de términos positivos, <math>a_1=3\;</math> y <math>a_3 = 6\;</math>. | + | En una progresión geométrica de términos positivos, <math>a_1=3\;</math> y <math>a_3 = 6\;</math>. |
| - | :Halla <math>a_n\;</math>, <math>a_{20}\;</math> y <math>a_{21}\;</math>. | + | Halla <math>a_n\;</math>, <math>a_{20}\;</math> y <math>a_{21}\;</math>. |
| |sol= | |sol= | ||
| - | :<math>a_3=a_1 \cdot r^2 \rightarrow 6 = 3 \cdot r^2 \rightarrow r^2=\cfrac{6}{3}=2 \rightarrow r=\pm \sqrt{2}</math> | + | <math>a_3=a_1 \cdot r^2 \rightarrow 6 = 3 \cdot r^2 \rightarrow r^2=\cfrac{6}{3}=2 \rightarrow r=\pm \sqrt{2}</math> |
| - | :Como la progresión es de términos positivos, sólo nos vale el valor posivo: {{sube|porcentaje=20%|contenido=<math>r=\sqrt{2}</math>}}. | + | Como la progresión es de términos positivos, sólo nos vale el valor posivo: {{sube|porcentaje=20%|contenido=<math>r=\sqrt{2}</math>}}. |
| {{p}} | {{p}} | ||
| - | :<math>a_n= a_1 \cdot r^{n-1} = 3 \cdot (\sqrt{2})^{n-1}</math> | + | <math>a_n= a_1 \cdot r^{n-1} = 3 \cdot (\sqrt{2})^{n-1}</math> |
| - | :<math>a_{20} = 3 \cdot (\sqrt{2})^{20-1} = 3 \cdot (\sqrt{2})^{19} = 3 \cdot 2^9 \cdot \sqrt{2} =1536 \sqrt{2}</math> | + | <math>a_{20} = 3 \cdot (\sqrt{2})^{20-1} = 3 \cdot (\sqrt{2})^{19} = 3 \cdot 2^9 \cdot \sqrt{2} =1536 \sqrt{2}</math> |
| - | :<math>a_{21} = 3 \cdot (\sqrt{2})^{21-1} = 3 \cdot (\sqrt{2})^{20} = 3 \cdot 2^{10} =3072</math> | + | <math>a_{21} = 3 \cdot (\sqrt{2})^{21-1} = 3 \cdot (\sqrt{2})^{20} = 3 \cdot 2^{10} =3072</math> |
| }} | }} | ||
| Línea 49: | Línea 49: | ||
| {{Ejemplo|titulo=Ejercicio resuelto: ''Suma de términos de una progresión geométrica'' | {{Ejemplo|titulo=Ejercicio resuelto: ''Suma de términos de una progresión geométrica'' | ||
| |enunciado={{p}} | |enunciado={{p}} | ||
| - | :Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año? | + | Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año? |
| |sol= | |sol= | ||
| - | :Al comenzar el primer año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^5</math> al final del quinto año. | + | Al comenzar el primer año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^5</math> al final del quinto año. |
| - | :Al comenzar el segundo año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^4</math> al final del quinto año. | + | Al comenzar el segundo año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^4</math> al final del quinto año. |
| - | :Al comenzar el tercer año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^3</math> al final del quinto año. | + | Al comenzar el tercer año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^3</math> al final del quinto año. |
| - | :Al comenzar el cuarto año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^2</math> al final del quinto año. | + | Al comenzar el cuarto año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^2</math> al final del quinto año. |
| - | :Al comenzar el quinto año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^1</math> al final del quinto año. | + | Al comenzar el quinto año ingreso 1000 €, que se transforman en <math>1000 \cdot 1.04^1</math> al final del quinto año. |
| {{p}} | {{p}} | ||
| - | :Si sumamos todas esas cantidades: | + | Si sumamos todas esas cantidades: |
| {{p}} | {{p}} | ||
| <center><math>1000 \cdot 1.04^1 + 1000 \cdot 1.04^2 + 1000 \cdot 1.04^3 + 1000 \cdot 1.04^4 + 1000 \cdot 1.04^5</math></center> | <center><math>1000 \cdot 1.04^1 + 1000 \cdot 1.04^2 + 1000 \cdot 1.04^3 + 1000 \cdot 1.04^4 + 1000 \cdot 1.04^5</math></center> | ||
| {{p}} | {{p}} | ||
| - | :estaremos sumando los cinco primeros términos de una progresión geométrica con <math>a_1= 1000 \cdot 1.04</math> y <math>r= 1.04\;</math> | + | estaremos sumando los cinco primeros términos de una progresión geométrica con <math>a_1= 1000 \cdot 1.04</math> y <math>r= 1.04\;</math> |
| {{p}} | {{p}} | ||
| <center><math>S_5 = \cfrac{a_1 \cdot (r^5 - 1)}{r-1} = \cfrac{1000 \cdot 1.04 \cdot (1.04^5 - 1)}{1.04 -1} = 5632.98</math> €</center> | <center><math>S_5 = \cfrac{a_1 \cdot (r^5 - 1)}{r-1} = \cfrac{1000 \cdot 1.04 \cdot (1.04^5 - 1)}{1.04 -1} = 5632.98</math> €</center> | ||
Revisión de 15:48 14 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 68)
Progresiones geométricas
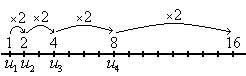
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija,  , que llamaremos razón.
, que llamaremos razón.
Escrito en forma recursiva:
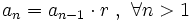
Por ejemplo, la sucesión 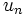 :
:
es una progresión geométrica de razón 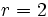 .
.
Progresiones geométricas: definición y ejemplos.
Halla el quinto término de la siguiente progresión geométrica: 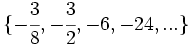
Halla el término 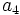 de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Actividades en las que aprenderás el concepto de progresión geométrica y a cómo identificarlas.
Extiende sucesiones geométricas.
Extiende sucesiones geométricas con términos negativos y racionales.
Fórmulas recursivas para sucesiones geométricas.
Término general de una progresión geométrica
Término general de una progresión geométrica
El término general, 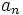 , de una progresión geométrica de razón
, de una progresión geométrica de razón  es:
es:
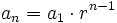
En efecto, de forma intuitiva:
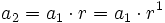

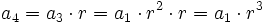
........................
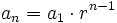
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
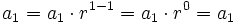
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
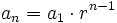 . [1]
. [1]Por ser una progresión geométrica cada término se obtiene multiplicando por r el anterior término:
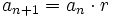 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n \cdot r \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 \cdot r^{n-1} \cdot r =a_1 \cdot r^{((n+1)-1)}](/wikipedia/images/math/b/5/0/b50e2fb51571873946095ab7579f8b90.png)
- Definición de progresión geométrica.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones geométricas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Término general de una progresión geométrica: Obtención y ejemplos.
- Definición de progresión geométrica.
- Ejemplos.
- Término general de una progresión geométrica.
Una progresión geométrica tiene como término general 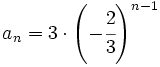 , halla el término
, halla el término 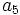 .
.
Halla el término general y la forma recursiva de la siguiente progresión geométrica: {168, 84, 42, , 21, ...}.
Halla la fórmula recursiva a partir del término general 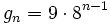 .
.
Problema sobre progresiones geométricas.
Actividades en las que aprenderás a obtener el término general de una progresión geométrica.
Progresiones geométricas.
Usa el término general de una progresión geométrica.
Halla el término general de una progresión geométrica.
Convertir formas recursivas y explícitas de sucesiones geométricas.
Problemas verbales con progresiones geométricas.
Ejercicio resuelto: Progresión geométrica
En una progresión geométrica de términos positivos, 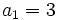 y
y 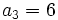 .
Halla
.
Halla  ,
, 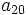 y
y 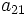 .
.
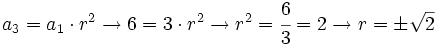
Como la progresión es de términos positivos, sólo nos vale el valor posivo: 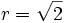 .
.
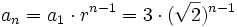
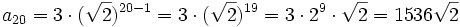
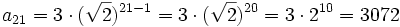
Encuentra el término general de una progresión geométrica dada.
Ejercicio resuelto: Progresión geométrica
En una progresión geométrica de términos positivos, 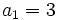 y
y 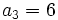 .
Halla
.
Halla  ,
, 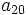 y
y 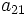 .
.
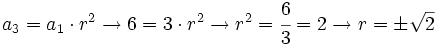
Como la progresión es de términos positivos, sólo nos vale el valor posivo: 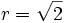 .
.
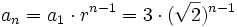
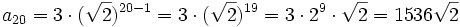
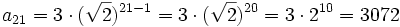
Ejercicios propuestos
|
Ejercicios propuestos: Término general de una progresión geométrica |
(Pág. 70)
Suma de términos de una progresión geométrica
Suma de términos de una progresión geométrica
La suma de los n primeros términos de una progresión geométrica es:
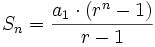
Efectuamos la siguiente resta:
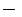
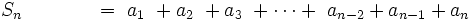
- ______________________________________________________________________________

por tanto:
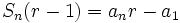
y despejando
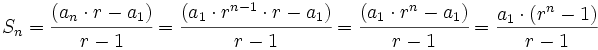
Actividades en las que aprenderás a obtener de los "n" primeros términos de una progresión geométrica.
Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.
Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.
Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
Suma los n primeros términos de progresión geométrica dada.
Ejercicio resuelto: Suma de términos de una progresión geométrica
Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año?
Se trata de un problema típico de aritmética comercial de anualidades de capitalización:
Al comenzar el primer año ingreso 1000 €, que se transforman en 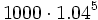 al final del quinto año.
al final del quinto año.
Al comenzar el segundo año ingreso 1000 €, que se transforman en 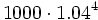 al final del quinto año.
al final del quinto año.
Al comenzar el tercer año ingreso 1000 €, que se transforman en 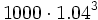 al final del quinto año.
al final del quinto año.
Al comenzar el cuarto año ingreso 1000 €, que se transforman en 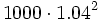 al final del quinto año.
al final del quinto año.
Al comenzar el quinto año ingreso 1000 €, que se transforman en 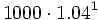 al final del quinto año.
al final del quinto año.
Si sumamos todas esas cantidades:
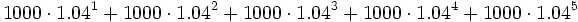
estaremos sumando los cinco primeros términos de una progresión geométrica con 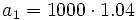 y
y 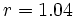
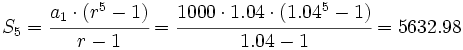 €
€Anualidades de capitalización son cantidades fijas que se entregan al principio de cada año para su colocación a interés compuesto con objeto de llegar a constituir un capital al cabo de un determinado número de años.
Anualidades de amortización son pagos fijos que se entregan al final de cada año para su colocación a interés compuesto, con objeto de llegar a extinguir o amortizar una deuda juntamente con sus intereses, en un determinado número de años.
Ejercicio resuelto: Suma de términos de una progresión geométrica
Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año?
Al comenzar el primer año ingreso 1000 €, que se transforman en 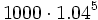 al final del quinto año.
al final del quinto año.
Al comenzar el segundo año ingreso 1000 €, que se transforman en 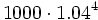 al final del quinto año.
al final del quinto año.
Al comenzar el tercer año ingreso 1000 €, que se transforman en 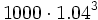 al final del quinto año.
al final del quinto año.
Al comenzar el cuarto año ingreso 1000 €, que se transforman en 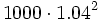 al final del quinto año.
al final del quinto año.
Al comenzar el quinto año ingreso 1000 €, que se transforman en 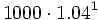 al final del quinto año.
al final del quinto año.
Si sumamos todas esas cantidades:
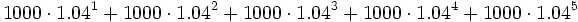
estaremos sumando los cinco primeros términos de una progresión geométrica con 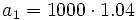 y
y 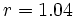
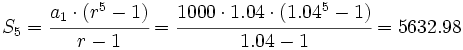 €
€Ejercicios propuestos
|
Ejercicios propuestos: Suma de términos de una progresión geométrica |
(Pág. 71)
Suma de los infinitos términos de una progresión geométrica
Suma de los infinitos términos de una progresión geométrica
La suma de todos los términos de una progresión geométrica en la que su razón verifica que 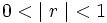 se obtiene así:
se obtiene así:
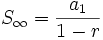
Para la demostración se requiere del concepto de límite. Véase: Algunos límites importantes.
Actividades en las que aprenderás a obtener la suma de todos los términos de una progresión geométrica, siempre que ésto sea posible.
Fórmula de la suma de todos los términos de una progresión geométrica. Ejemplos.
Fórmula de la suma de los infinitos términos de una progresión geométrica. Ejemplos.
Ejercicios propuestos
|
Ejercicios propuestos: Suma de los infinitos términos de una progresión geométrica |
Producto de términos de una progresión geométrica
Producto de "n" términos de una progresión geométrica
El producto de los n primeros términos de una progresión geométrica es:
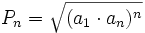
Véase en el siguiente videotutorial.
Actividades en las que aprenderás a obtener el producto de los "n" primeros términos de una progresión geométrica.
Demostración de la fórmula del producto de n términos de una progresión geométrica
Actividades
|
Actividad: Progresiones geométricas Dada la sucesión {1, 1/2, 1/4, 1/8, ...}: a) Halla el término general. b) Halla el término 10. c) Halla el producto de los 10 primeros términos. d) Halla la suma de los términos del 10 al 15. e) Halla la suma de los infinitos términos. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 1/2, 1/4, 1/8, ...} b) {2^(-n+1)} for n=10 c) product {2^(-n+1)} for n=1 to 10 d) sum {2^(-n+1)} for n=10 to 15 d) sum {2^(-n+1)} for n=1 to oo
|
Obtención del término general y de la suma de los términos de las siguientes progresiones geométricas:
- a) Dada la progresión 2, 6, 18, 54, ..., halla su término general y la suma de los 20 primeros términos.
- b) Dada la progresión 8, 4, 2, 1, ... , halla su término general y la suma de todos sus términos.
El primer término de una progresión geométrica es 3 y la razón 2. Halla el quinto término y la suma de los ocho primeros términos.
El primer término de una progresión geométrica es -4 y el sexto término es 972. Halla la razón.
El cuarto término de una progresión geométrica es 8 y el noveno término es 1/4. Halla la suma de todos los términos de la progresión.
Determina tres números en progresión geométrica de manera que su producto sea 216 y su suma 19.
- Determina la progresión geométrica tal que
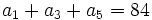 y
y 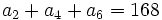 .
.
- Determina tres números en progresión geométrica de manera que su suma sea 28 y la diferencia entre el tercero y el primero sea 12.
Determina tres números en progresión geométrica de manera que al sumar 2 al segundo resulta una progresión aritmética, y al sumar 9 al tercero de ésta última resulta una progresión geométrica.
Sea {an} una progresión geométrica de razón r. Determina:
-
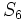 sabiendo que
sabiendo que 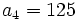 y
y 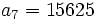
-
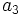 sabiendo que r=2 y
sabiendo que r=2 y 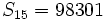
- n sabiendo que
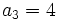 , r=2 y
, r=2 y 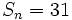
Resuelve la ecuación: 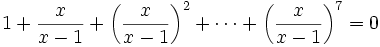
Fórmula para la obtención del capital final en un sistema de capitalización o interés compuesto como aplicación de las progresiones geométricas.
- Determina el montante obtenido al invertir 1500 € durante 5 años al 9% de interés compuesto anual.
- Determina el capital C que debe invertirse durante 4 años al 7% de interés compuesto anual para obtener un montante de 3000 €.
- Si el montante obtenido al cabo de 5 años por un capital de 1350 € es de 1702.57 €, calcula el tipo de interés compuesto anual.
- Si el interés compuesto anual es del 5%, calcula el tiempo que ha estado invertido un capital de 2100 € si el montante obtenido es de 2954.91 €
Fórmula para la obtención del capital final en un sistema de pensiones basado en un sistema de capitalización compuesta como aplicación de las progresiones geométricas.
Fórmula para la obtención de la anualidad que hay que pagar al final de cada año para amortizar un préstamo a un cierto interés.
En una progresión geométrica de razón 3, el cuarto término vale 13. Halla el término general.
En una progresión geométrica de razón 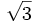 , el tercer término vale
, el tercer término vale 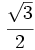 . Halla el sexto término y la suma de los seis primeros términos.
. Halla el sexto término y la suma de los seis primeros términos.
Ejercicios.