Números racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:40 18 abr 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:58 18 abr 2007 Coordinador (Discusión | contribuciones) (→Fracciones equivalentes) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| ===Fracciones propias e impropias=== | ===Fracciones propias e impropias=== | ||
| ===Fracciones equivalentes=== | ===Fracciones equivalentes=== | ||
| - | {{Caja Amarilla|texto='''Fracciones equivalentes''' son las que representan el mismo valor.}}{{p}} | + | {{Caja Amarilla|texto='''Fracciones equivalentes''' son aquelllas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.}}{{p}} |
| - | Las fracciones equivalentes tienen distinto numerador y denominador, pero valen lo mismo. Cada fracción tiene infinitas fracciones equivalentes a ella.{{p}} | + | Cada fracción tiene infinitas fracciones equivalentes a ella. Podemos obtenerlas multiplicando numerador y denominador por un mismo número. Por ejemplo, <math>\cfrac{3}{5}=\cfrac{6}{10}=\cfrac{9}{15}</math>{{p}} |
| {{Caja Amarilla|texto=Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | {{Caja Amarilla|texto=Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | ||
| <center><math>\cfrac{a}{b}=\cfrac{c}{d} \quad\Leftrightarrow\quad a \cdot d=b \cdot c</math>}}</center>{{p}} | <center><math>\cfrac{a}{b}=\cfrac{c}{d} \quad\Leftrightarrow\quad a \cdot d=b \cdot c</math>}}</center>{{p}} | ||
| Línea 19: | Línea 19: | ||
| :#[http://descartes.cnice.mecd.es/1y2_eso/fracciones/equival2.htm Agrupa las fracciones equivalentes] | :#[http://descartes.cnice.mecd.es/1y2_eso/fracciones/equival2.htm Agrupa las fracciones equivalentes] | ||
| }}{{p}} | }}{{p}} | ||
| + | |||
| ===Simplificar fracciones. Fracciones irreducibles=== | ===Simplificar fracciones. Fracciones irreducibles=== | ||
| {{Caja Amarilla|texto='''Simplificar una fracción''' consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debermos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1. En tal caso, la fracción es '''irreducible'''.}} | {{Caja Amarilla|texto='''Simplificar una fracción''' consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debermos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1. En tal caso, la fracción es '''irreducible'''.}} | ||
Revisión de 19:58 18 abr 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones | Fracciones | WIRIS Geogebra Calculadora {{{enlaces}}} |
Tabla de contenidos |
Definiciones
Fracciones propias e impropias
Fracciones equivalentes
Fracciones equivalentes son aquelllas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.
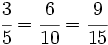
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
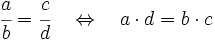
Actividades Interactivas: Fracciones equivalentes
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debermos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1. En tal caso, la fracción es irreducible.
Actividades Interactivas: Simplificar de fracciones

