Números racionales
De Wikipedia
| Revisión de 19:58 18 abr 2007 Coordinador (Discusión | contribuciones) (→Fracciones equivalentes) ← Ir a diferencia anterior |
Revisión de 21:01 18 abr 2007 192.168.2.3 (Discusión) (→Definiciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Definiciones== | ==Definiciones== | ||
| + | Así como los números naturales surgen para expresar cantidades que se refieren a objetos enteros, las fracciones son consecuencia de expresar cantidades que se refieren a partes de un objeto dividido en partes iguales. | ||
| + | {{p}} {{AI|titulo=Actividades Interactivas: ''Fracciones''|enunciado= | ||
| + | :#[http://descartes.cnice.mecd.es/1y2_eso/fracciones/definic1.htm Definición] | ||
| + | :#[http://descartes.cnice.mecd.es/1y2_eso/fracciones/definic2.htm Representación gráfica] | ||
| + | }}{{p}} | ||
| + | Si el numerador es divisible por el denominador, la fracción representa a un número entero. Al conjunto de todas las fracciones también se le llama conjunto de '''números racionales'''. Lo representaremos por <math>\mathbb{Q}</math>. Según lo dicho, los racionales contienen a los enteros y éstos a los naturales. | ||
| + | <center><math>\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}</math></center> | ||
| ===Fracciones propias e impropias=== | ===Fracciones propias e impropias=== | ||
| + | {{Caja Amarilla|texto='''Fracciones propias''' son aquellas cuyo numerador es menor que el denominador. Son menores que 1.<br> '''Fracciones impropias''' son aquellas cuyo numerador es mayor que el denominador. Son mayores que 1.}} | ||
| + | {{p}} {{AI|titulo=Actividades Interactivas: ''Fracciones propias e impropias''|enunciado= | ||
| + | :#[http://descartes.cnice.mecd.es/1y2_eso/fracciones/valor1.htm Valor de una fracción] | ||
| + | }}{{p}} | ||
| ===Fracciones equivalentes=== | ===Fracciones equivalentes=== | ||
| - | {{Caja Amarilla|texto='''Fracciones equivalentes''' son aquelllas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.}}{{p}} | + | {{Caja Amarilla|texto='''Fracciones equivalentes''' son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.}}{{p}} |
| Cada fracción tiene infinitas fracciones equivalentes a ella. Podemos obtenerlas multiplicando numerador y denominador por un mismo número. Por ejemplo, <math>\cfrac{3}{5}=\cfrac{6}{10}=\cfrac{9}{15}</math>{{p}} | Cada fracción tiene infinitas fracciones equivalentes a ella. Podemos obtenerlas multiplicando numerador y denominador por un mismo número. Por ejemplo, <math>\cfrac{3}{5}=\cfrac{6}{10}=\cfrac{9}{15}</math>{{p}} | ||
| {{Caja Amarilla|texto=Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | {{Caja Amarilla|texto=Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden. | ||
Revisión de 21:01 18 abr 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones | Fracciones | WIRIS Geogebra Calculadora {{{enlaces}}} |
Tabla de contenidos |
Definiciones
Así como los números naturales surgen para expresar cantidades que se refieren a objetos enteros, las fracciones son consecuencia de expresar cantidades que se refieren a partes de un objeto dividido en partes iguales.
Si el numerador es divisible por el denominador, la fracción representa a un número entero. Al conjunto de todas las fracciones también se le llama conjunto de números racionales. Lo representaremos por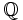 
. Según lo dicho, los racionales contienen a los enteros y éstos a los naturales.
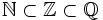
Fracciones propias e impropias
Fracciones propias son aquellas cuyo numerador es menor que el denominador. Son menores que 1.
Fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Son mayores que 1.
Fracciones equivalentes
Fracciones equivalentes son aquellas que, aún teniendo distinto numerador y denominador, tienen el mismo valor.
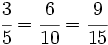
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
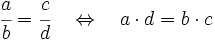
Actividades Interactivas: Fracciones equivalentes
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debermos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1. En tal caso, la fracción es irreducible.
Actividades Interactivas: Simplificar de fracciones
