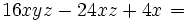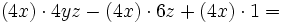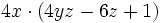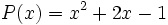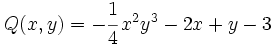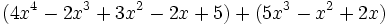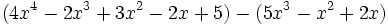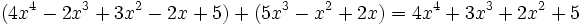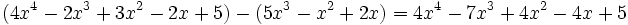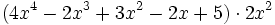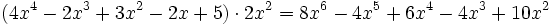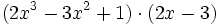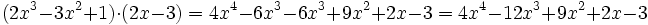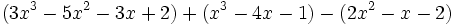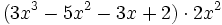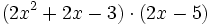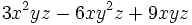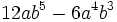Polinomios
De Wikipedia
| Revisión de 13:26 25 oct 2016 Coordinador (Discusión | contribuciones) (→Suma y resta de polinomios) ← Ir a diferencia anterior |
Revisión de 13:28 25 oct 2016 Coordinador (Discusión | contribuciones) (→Operaciones con polinomios) Ir a siguiente diferencia → |
||
| Línea 32: | Línea 32: | ||
| |titulo=Ejemplo: ''Producto de un monomio por un polinomio'' | |titulo=Ejemplo: ''Producto de un monomio por un polinomio'' | ||
| |enunciado= | |enunciado= | ||
| - | :Calcula el producto: <math>(4x^4 - 2x^3 + 3x^2 - 2x + 5 ) \cdot 2x^2 \;\!</math> | + | Calcula el producto: <math>(4x^4 - 2x^3 + 3x^2 - 2x + 5 ) \cdot 2x^2 \;\!</math> |
| |sol= | |sol= | ||
| <math>(4x^4 - 2x^3 + 3x^2 - 2x + 5 ) \cdot 2x^2 = 8x^6-4x^5+6x^4-4x^3+10x^2 \;\!</math> | <math>(4x^4 - 2x^3 + 3x^2 - 2x + 5 ) \cdot 2x^2 = 8x^6-4x^5+6x^4-4x^3+10x^2 \;\!</math> | ||
| Línea 43: | Línea 43: | ||
| |titulo=Ejemplo: ''Producto de polinomios'' | |titulo=Ejemplo: ''Producto de polinomios'' | ||
| |enunciado= | |enunciado= | ||
| - | :Calcula el producto: <math>(2x^3 - 3x^2 +1) \cdot (2x-3)\;\!</math> | + | Calcula el producto: <math>(2x^3 - 3x^2 +1) \cdot (2x-3)\;\!</math> |
| |sol= | |sol= | ||
| Línea 49: | Línea 49: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{wolfram desplegable|titulo=Operaciones con polinomios|contenido= | ||
| {{wolfram | {{wolfram | ||
| |titulo=Actividad: ''Operaciones con polinomios'' | |titulo=Actividad: ''Operaciones con polinomios'' | ||
| Línea 54: | Línea 55: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | :Haz las siguientes operaciones con polinomios: | + | Haz las siguientes operaciones con polinomios: |
| :a) <math>(3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2)\!</math> | :a) <math>(3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2)\!</math> | ||
| Línea 63: | Línea 64: | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :a) {{consulta|texto=expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2)}} | + | a) {{consulta|texto=expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2)}} |
| - | :b) {{consulta|texto=expand (3x^3-5x^2-3x+2)*2x^2}} | + | b) {{consulta|texto=expand (3x^3-5x^2-3x+2)*2x^2}} |
| - | :c) {{consulta|texto=expand (2x^2+2x-3)*(2x-5)}} | + | c) {{consulta|texto=expand (2x^2+2x-3)*(2x-5)}} |
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| }} | }} | ||
| - | + | }} | |
| + | {{p}} | ||
| ===Sacar factor común=== | ===Sacar factor común=== | ||
| La propiedad distributiva sirve para simplificar expresiones '''sacando factor común'''. Veamos un ejemplo | La propiedad distributiva sirve para simplificar expresiones '''sacando factor común'''. Veamos un ejemplo | ||
| Línea 77: | Línea 79: | ||
| |titulo=Ejemplo: ''Sacar factor común'' | |titulo=Ejemplo: ''Sacar factor común'' | ||
| |enunciado= | |enunciado= | ||
| - | :Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> | + | Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> |
| |sol= | |sol= | ||
| El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | ||
| Línea 85: | Línea 87: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{wolfram desplegable|titulo=Sacar factor común|contenido= | ||
| {{wolfram | {{wolfram | ||
| |titulo=Actividad: ''Sacar factor común'' | |titulo=Actividad: ''Sacar factor común'' | ||
| Línea 98: | Línea 101: | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :a) {{consulta|texto=factor 3x^2*y*z-6x*y^2*z+9x*y*z}} | + | a) {{consulta|texto=factor 3x^2*y*z-6x*y^2*z+9x*y*z}} |
| - | :b) {{consulta|texto=factor 12a*b^5-6a^4*b^3}} | + | b) {{consulta|texto=factor 12a*b^5-6a^4*b^3}} |
| {{widget generico}} | {{widget generico}} | ||
| + | }} | ||
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 13:28 25 oct 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Algebra (1º ESO) | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Polinomios
|
Para nombrar un polinomio usaremos una letra mayúscula (lo normal es usar las letras: P, Q, R, S, ...) seguida de las variables que forman parte del polinomio, entre paréntesis.
Por ejemplo:
a) El polinomio 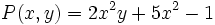 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
b) El polinomio 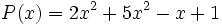 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 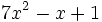 . Es de grado 2.
. Es de grado 2.
c) Los polinomios constantes, como por ejemplo 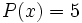 , tienen grado 1. Sin embargo, el polinomio nulo,
, tienen grado 1. Sin embargo, el polinomio nulo, 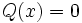 , tiene grado cero.
, tiene grado cero.
d) Los polinomios 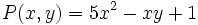 y
y 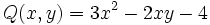 son semejantes.
son semejantes.
e) Los polinomios 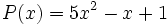 y
y 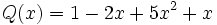 son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
son iguales, porque al reducir el segundo y reordenar sus monomios, queda igual al primero.
Tutorial en el que se dan las definiciones básicas del álgebra: expresión algebraica, monomios, polinomios, grado, término independiente, coeficientes...
Polinomios. Grado de un polinomio. Ejemplos.
Polinomios. Grado de un polinomio. Ejemplos.
Aprende a calcular el grado relativo y absoluto de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Aprende a calcular el grado relativo y absoluto de un monomio y de un polinomio.
Nota: Al "grado absoluto" de un polinomio se le llama simplemente "grado" del polinomio.
Polinomios: términos y tipos de polinomios. Polinomios nulos.
Forma reducida de un polinomio. Grado. Polinomios iguales y semejantes.
- Polinomios ordenados, completos / incompletos, homogéneos / heterogéneos.
- Valor numérico de un polinomio.
Polinomios. Monomios. Grado y término independiente de un polinomio.
1) Indica de qué tipo son los polinomios siguientes, atendiendo al número de términos que tienen:
- a)
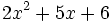
- b)
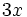
- c)
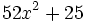
- d)
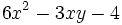
- e)
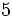
- f)
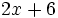
2) Expresa en forma reducida los siguientes polinomios:
- a)
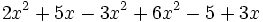
- b)
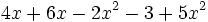
- c)
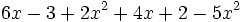
- d)
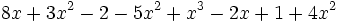
3) Indica el grado de cada polinomio:
- a)
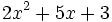 ; b)
; b) 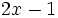 ; c)
; c) 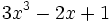
- d)
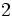 ; e)
; e) 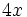 ; f)
; f) 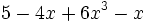
- g)
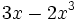 ; h)
; h) 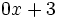 ; i)
; i) 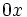
4) Indica cuáles de estos polinomios son iguales:
- a)
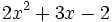 ; b)
; b) 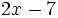 ; c)
; c) 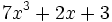 ; d)
; d) 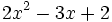
- e)
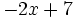 ; f)
; f) 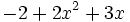 ; g)
; g) 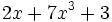 ; h)
; h) 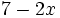
- i)
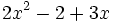 ; j)
; j) 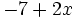 ; k)
; k) 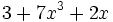 ; l)
; l) 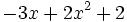
5) Indica cuáles de estos polinomios son semejantes entre sí:
- a)
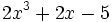 ; b)
; b) 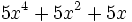 ; c)
; c) 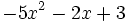
- d)
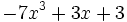 ; e)
; e) 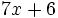 ; f)
; f) 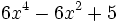
- g)
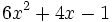 ; h)
; h) 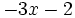
6) Ordena, tanto de forma creciente como decreciente, e indica el grado de los siguientes polinomios:
- a)
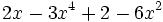
- b)
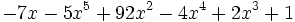
- c)
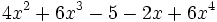
- d)
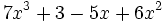
- e)
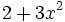
- f)
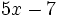
7) Clasificar polinomios en homogéneos/heterogéneos.
- a)
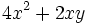
- b)
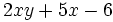
- c)
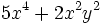
- d)
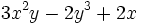
- e)
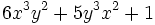
- f)
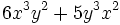
- g) 5x3 − 6y3
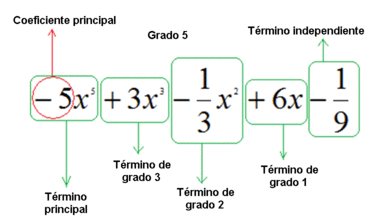
Dado el polinomio 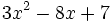 , identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
, identifica sus términos junto con el coeficiente y exponente de cada uno de ellos.
Escribe un polinomio que exprese el valor de "p" billetes de 20 pesos, "q" monedas de 10 pesos y "r" monedas de 5 pesos.
Elementos y grado de un polinomio.
Expresiones algebraicas: monomios y polinomios.
- Actividad en la que deberás encontrar la expresión polinómica adecuada para cada situación.
- Actividad en la que deberás construir un polinomio conocida cierta información sobre su grado y los coeficientes de sus términos.
- Actividad en la que deberás encontrar el valor de algún coeficiente de un polinomio.
- Actividad en la que aprenderás a escribir polinomios en su forma usual.
- Actividad en la que deberás decir cual es el coeficiente de cada grado de un polinomio.
Actividad sobre polinomios.
Operaciones con polinomios
Suma y resta de polinomios
Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.
Producto de un monomio por un polinomio
Para multiplicar un monomio por un polinomio, se multiplica el monomio por cada término del polinomio y se suman los resultados.
Producto de polinomios
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.
|
Actividad: Operaciones con polinomios Haz las siguientes operaciones con polinomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2) b) expand (3x^3-5x^2-3x+2)*2x^2 c) expand (2x^2+2x-3)*(2x-5) |
Sacar factor común
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
Saca factor común en la expresión 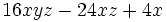
El factor común, que se repite en los tres sumandos, es
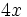 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 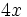 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso: