Posición relativa de dos rectas
De Wikipedia
| Revisión de 20:09 9 nov 2016 Coordinador (Discusión | contribuciones) (→Posición relativa de dos rectas) ← Ir a diferencia anterior |
Revisión de 11:29 10 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| ==Posición relativa de dos rectas== | ==Posición relativa de dos rectas== | ||
| {{Posición relativa de dos rectas}} | {{Posición relativa de dos rectas}} | ||
| - | + | {{p}} | |
| + | ==Perpendicularidad entre rectas== | ||
| + | {{Perpendicularidad entre rectas}} | ||
| + | {{p}} | ||
| ==Ejercicios== | ==Ejercicios== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 11:29 10 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ejercicios Ecuación pto-pendiente Ecuaciones de la recta | WIRIS Geogebra Calculadora Función lineal Recta |
Posición relativa de dos rectas
Dos rectas del plano pueden ocupar una de las tres posiciones siguientes:
- Secantes: Se cortan en un punto.
- Paralelas: No se cortan.
- Coincidentes: Tienen infinitos puntos en común, son la misma recta.
Procedimiento
Para determinar la posición relativa de dos rectas podemos recurrir a:
1. Resolver el sistema formado por las dos ecuaciones y dependiendo del número de soluciones del sistema tendremos:
- 1 solución: Las rectas son secantes.
- 0 soluciones: Las rectas son paralelas.
- Infinitas soluciones: Las rectas son coincidentes.
2. Comparar las pendientes y las ordenadas en el origen de cada recta:
- Distintas pendientes: Las rectas son secantes.
- Igual pendiente y distinta ordenada en el origen: Las rectas son paralelas.
- Igual pendiente e igual ordenada en el origen: Las rectas son coincidentes.
Paralelismo entre rectas del plano Descripción: En esta escena podrás ver e interactuar con dos rectas paralelas y ver que las caracteriza.
Actividades en las que aprenderás a averiguar la posición relativa de dos rectas dadas en forma explícita.
Actividades en las que aprenderás a averiguar la posición relativa de dos rectas dadas en forma general.
Perpendicularidad entre rectas
Propiedad
Dos rectas, con pendientes m y m', son perpendiculares si y sólo si sus pendientes son inversas y opuestas simultaneamente:
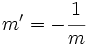
O equivalentemente, cuando el producto de ambas pendientes es igual a -1:
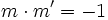
Perpendicularidad entre rectas Descripción: En esta escena podrás ver e interactuar con dos rectas perpendiculares y ver que las caracteriza.
Ejercicios
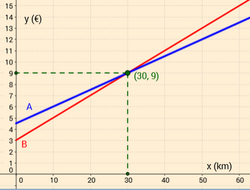
 Problema: Posición relativa de dos rectas 1. Una empresa de transporte A tiene las siguientes tarífas: 0,20 € por kilómetro de recorrido y 3 € por paquete. Las tarifas de otra empresa B son: 0,15 € por kilómetro y 4,50 € por paquete.
Solución:
|
